
- •1. Матрицы. Матрицы частного вида.
- •2.Сложение матриц, умножение на число, перемножение матриц.
- •3. Определители и их свойства.
- •4. Минор и алгебраическое дополнение элемента. Методы вычисления определителей. Разложение определителя по строкам и столбцам.
- •5. Невырожденная матрица, обратная матрица.
- •7. Системы линейных уравнений.
- •8. Методы решения системы n уравнений с n неизвестными: матричный, метод Крамера.
- •9. Метод Гаусса.
- •10. Исследование системы линейных уравнений общего вида. Теорема Кромекера-Капелли.
- •12. Модель Леонтьева. Продуктивные модели Леонтьева.
- •13. Основные понятия теории многочленов. Теории Безу. Основная теория алгебры. Разложение многочленов на многочлены.
- •14. Разложение правильной рациональной дроби на сумму простейших дробей.
- •15. Комплексные числа и действия над ними. Геометрическая интерпретация комплексного числа. Модуль и аргумент комплексного числа.
- •16. Алгебраическая, тригонометрическая и показательная форма записи комплексного числа. Формула Эйлера. Формула Муавра. Корни n-ой степени из комплексных чисел.
- •17. Векторная алгебра. Вектор на плоскости и в пространстве. Линейные операции над векторами. Скалярное произведение.
- •18. Линейное пространство. Линейная зависимость. Системы векторов и ее геометрический смысл.
- •19. Базис и размерность линейного пространства. Координаты вектора в данном базисе.
- •20. Скалярное произведение векторов в Rn. Евклидово пространство. Неравенства Коши-Буняковского. Длины векторов и угол между векторами в Rn.
- •21.Линейные преобразования пространства Rn. Линейный оператор и его матрица.
- •22. Квадратичные формы, их матрицы в данном базисе. Приведение квадратичной формы к нормальному виду, приведение квадратичной формы к каноническому виду.
- •23.Прямая линия на плоскости. Различные виды уравнений прямой на плоскости.
- •24, 25. Классификации кривых второго порядка. Эллипс, гипербола, парабола, их свойства и канонические уравнения.
- •26. Приведение общего уравнения кривой второго порядка к каноническому виду.
- •27. Плоскость в пространстве. Различные виды уравнений плоскости в пространстве.
- •28. Классификация поверхностей второго порядка.
- •29. Эллипсоиды, гиперболоиды, парабалоиды, их свойства и канонические уравнения.
- •30. Примеры экономико-математических моделей, приводящих к задачам линейного программирования. Основная задача линейного программирования.
- •31. Геометрическая интеграция задачи линейного программирования для двух переменных. Графический метод решения. Решение задачи линейного программирования методом перебора вершин.
- •32. Симплекс метод. Решение задач линейного программирования. Нахождение опорного плана, нахождение оптимального плана. Понятие о взаимно-двойственных задач.
- •33,34. Транспортная задача. Методы отыскания опорного плана транспортной задачи.
12. Модель Леонтьева. Продуктивные модели Леонтьева.
Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями. Математическая модель Леонтьева позволяет анализировать связь между отраслями. Xj – объём продукции i отрасли, валовый выпуск продукции i-ой отрасли. Xij – Объём продукции I отрасли, потребляемой j-ой при производстве. Yj – объём продукции i-ой отрасли предназначенной для реализации – конечный продукт. Работает балансовый принцип связи различных отраслей промышленности. Валовый выпуск i-ой отрасли должен быть равен сумме объемов потребления в производственной и непроизводственной сферах.
Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i-й
отрасли должен быть равен сумме объёмов потребления в производственной и непроизводственной сферах.
В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеют вид:
Xi=Xi1+Xi2+…+Xin+Yi. Эти уравнения называются соотношениями баланса. Модель Леонтьева называется продуктивной, если система имеет неотрицательное решение.
13. Основные понятия теории многочленов. Теории Безу. Основная теория алгебры. Разложение многочленов на многочлены.
![]() , где n – целое число,
коэффициенты
, где n – целое число,
коэффициенты ![]() – константы – коэффициенты многочлена.
Высшая степень x –
называется степенью многочлена. Два
многочлена равные если равны их
соответствующие коэффициенты(коэф. При
одинаковых степенях x).
Корнем многочлена называют такое
значение x, при котором
многочлен образуется в ноль. Теорема
Безу. При делении многочлена
– константы – коэффициенты многочлена.
Высшая степень x –
называется степенью многочлена. Два
многочлена равные если равны их
соответствующие коэффициенты(коэф. При
одинаковых степенях x).
Корнем многочлена называют такое
значение x, при котором
многочлен образуется в ноль. Теорема
Безу. При делении многочлена ![]() от x на двучлен x-
от x на двучлен x-![]() получается остаток равный значению
многочлена при x=
получается остаток равный значению
многочлена при x=![]() .
.
![]() , где остаток
, где остаток ![]() .
Следствие: Если
– корень многочлена, то многочлен
.
Следствие: Если
– корень многочлена, то многочлен ![]() делится на x-
без остатка. Основная теорема алгебры.
Всякий многочлен имеет по крайней
мере один корень. Пусть
делится на x-
без остатка. Основная теорема алгебры.
Всякий многочлен имеет по крайней
мере один корень. Пусть ![]() – корень многочлена
– корень многочлена ![]() .
.
![]() – таким образом многочлен n-ой
степени может быть представлен в виде
произведения n-линейных
множителей
– таким образом многочлен n-ой
степени может быть представлен в виде
произведения n-линейных
множителей ![]() ,
где
,
где ![]() – корни многочлена и const.
– корни многочлена и const.
![]() .
Разложение многочлена на линейные
множители
.
Разложение многочлена на линейные
множители ![]() Если
многочлен имеет целые корни, то они
содержатся среди делителей свободного
члена многочлена. Если корни многочлена
равны, то они называются кратными и
тогда разложение многочлена можно
представить в общем виде.
Если
многочлен имеет целые корни, то они
содержатся среди делителей свободного
члена многочлена. Если корни многочлена
равны, то они называются кратными и
тогда разложение многочлена можно
представить в общем виде.
14. Разложение правильной рациональной дроби на сумму простейших дробей.
Рассмотрим рациональную функцию (или рациональную дробь)
![]() .Здесь
.Здесь
![]() Pn(x)
и Qm(x) – многочлены степеней n и m
относительно переменной x. Если
Pn(x)
и Qm(x) – многочлены степеней n и m
относительно переменной x. Если
![]() ,
т.е. дробь неправильная, то её можно
представить в виде
,
т.е. дробь неправильная, то её можно
представить в виде
![]() (k<m) или, как говорят, выделить из нё
целую часть Pn-m(x).В результате интегрирование
неправильной дроби сводится к
интегрированию правильной дроби
(k<m) или, как говорят, выделить из нё
целую часть Pn-m(x).В результате интегрирование
неправильной дроби сводится к
интегрированию правильной дроби
![]() .Теорема.
Пусть
- правильная рациональная дробь (n<m),
а разложение Qm(x) на произведение
неприводимых множителей имеет вид
.Теорема.
Пусть
- правильная рациональная дробь (n<m),
а разложение Qm(x) на произведение
неприводимых множителей имеет вид
![]() ,
a,…,b – вещественные корни, x2+px+q, …,
x2+rx+s – квадратные трёхчлены, неразложимые
на вещественные множители. Тогда
,
a,…,b – вещественные корни, x2+px+q, …,
x2+rx+s – квадратные трёхчлены, неразложимые
на вещественные множители. Тогда
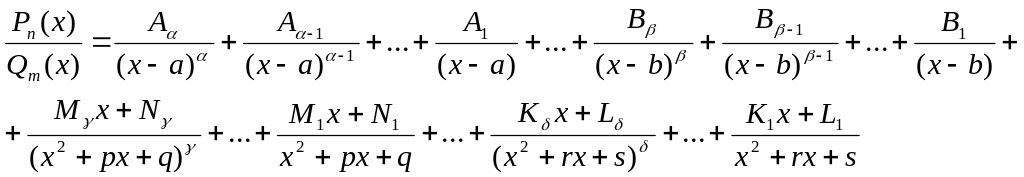
где Ai, Bi, Mi, Ni, Ki, Li – вещественные числа.
