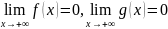- •Свойства модуля:
- •Числовая последовательность
- •Предел числовой последовательности
- •Свойства сходящихся последовательностей:
- •Верхний и нижний пределы последовательности.
- •Точки сгущения (предельные точки).
- •Определение предела функции по Гейне и Коши
- •Дифференцируемость функции в точке. Дифференциал функции. Его геометрический и физический смыслы.
- •Основные формулы дифференцирования элементарных функций.
- •Уравнение касательной прямой, в кривой, заданной параметрически.
- •3 Класса точек параметрически заданной кривой:
- •Гладкие функции и гладкие кривые на плоскости.
- •Старшие производные и дифференциалы функций.
- •Производные и дифференциалы старших порядков для сложных функций.
- •Теоремы о среднем для дифференцируемых функций.
- •Вычисление пределов с помощью правил Лопиталя.
- •Исследование локальных экстремумов функции.
- •Нахождение глобального экстремума функции на отрезке.
- •Асимптоты функции. Горизонтальные, вертикальные, наклонные.
Теоремы о среднем для дифференцируемых функций.
Теорема Ферма. Если функция задана в окрестности , непрерывна в этой окрестности, и в принимает либо самое наибольшее значение в , либо самое наименьшее, если в функция дифференцируема в широком смысле, то производная в этой точке обязательно равна 0.
Функция дифференцируема в точке в широком смысле, если в этой точке существует конечная или бесконечная (определенного знака) производная.
Правая и левая производные разного знака.
В теореме Ферма важно, чтобы функция была определена в двусторонней окрестности .
Теорема Ролля. определена на и удовлетворяет условиям:
непрерывна на
дифференцируема в широком смысле на
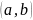
На концах отрезка функция принимает равные значения:

Тогда
существует хотя бы одна
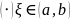 такая, что
такая, что
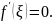
Inf и sup (2 случая: равны и не равны)
Все условия теоремы Ролля важны, если хотя бы одно условие нарушается, то вся теорема становится неверной.
Теорема Лагранжа. на удовлетворяет условиям:
на

дифференцируема в широком смысле на
Тогда
существует хотя бы одна
такая, что

 .
.
– дифференцируемая средняя Лагранжа.
Геометрический
смысл:
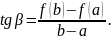
Рассмотрим новую
функцию
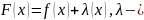 неопределенный множитель, на
функция удовлетворяет условиям теоремы
Ролля.
неопределенный множитель, на
функция удовлетворяет условиям теоремы
Ролля.
Следствия из теоремы Лагранжа:
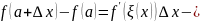 формула
конечных приращений для дифференцируемой
функции (точная).
формула
конечных приращений для дифференцируемой
функции (точная).
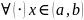 выполняется
теорема Лагранжа.
выполняется
теорема Лагранжа.
Если функция определена на промежутке и всюду внутри промежутка имеет производную, равную 0, то эта функция есть константа.
Если
 внутри промежутка имеют одинаковые
производные, то
внутри промежутка имеют одинаковые
производные, то
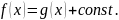
Теорема
Коши. Если
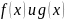 на
удовлетворяют условиям:
на
удовлетворяют условиям:
непрерывны на .
дифференцируемы на .
 .
.
Тогда
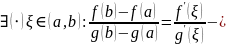 равенство Коши
равенство Коши
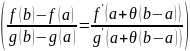 .
.
Теорема Лагранжа есть частный случай теоремы Коши.
Аналогично
теореме Лагранжа

Вычисление пределов с помощью правил Лопиталя.
Вычисление
пределов вида
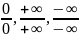 с помощью производных функций.
с помощью производных функций.
Теорема 1 (Правило Лопиталя №1). Пусть функции удовлетворяют условиям:
Определены и непрерывны в проколотой окрестности точки , причем в этой окрестности дифференцируемы.

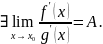
Тогда
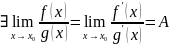 .
.
Доопределим функции
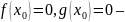 удовлетворяют
условиям теоремы Коши на отрезках
удовлетворяют
условиям теоремы Коши на отрезках
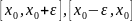 .
.
Теорема 2 (Правило Лопиталя №2). Пусть функции удовлетворяют условиям:
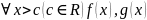 определены
и дифференцируемы
определены
и дифференцируемы
(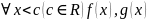 определены
и дифференцируемы)
определены
и дифференцируемы)
(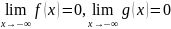 )
)
(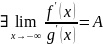 )
)
Тогда
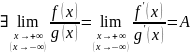 .
.
Рассмотреть функции
на интервале
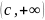 ,
,
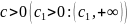 .
Замена переменной
.
Замена переменной
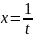 ,
правило Лопиталя №1.
,
правило Лопиталя №1.
Теорема 3 (Правило Лопиталя №3). Пусть функции удовлетворяют условиям:
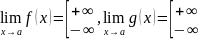
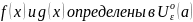 ,
непрерывны и дифференцируемы.
,
непрерывны и дифференцируемы.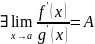
Тогда
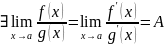 .
.
Аналогично правилу Лопиталя №1.
Теорема 4 (Правило Лопиталя №4). Пусть функции удовлетворяют условиям:

на
 непрерывны и дифференцируемы.
непрерывны и дифференцируемы.
Тогда .
Аналогично правилу Лопиталя №2.
Формула Тейлора для многочлена.
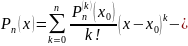 формула
Тейлора для многочлена.
формула
Тейлора для многочлена.
 ее
частный случай
ее
частный случай
 – формула Макларена.
– формула Макларена.
На практике эти формулы используются для записи многочлена по соответствующим степеням.
Формула Тейлора для произвольной функции. Локальная теорема Тейлора.
Теорема.
(Локальная теорема Тейлора) Если
определена в
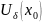 ,
имеет в
первые
производных,
,
имеет в
первые
производных,
 ,
тогда
,
тогда
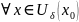 справедлива формула (формула Тейлора):
справедлива формула (формула Тейлора):
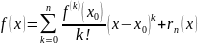 ,
где
,
где
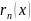 – остаточный член формулы Тейлора, а
все первые
– остаточный член формулы Тейлора, а
все первые
 членов – многочлен Тейлора -го порядка
членов – многочлен Тейлора -го порядка
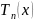 .
.
В
формуле Пеано остаточный член записывается
в виде
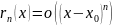
При
 ,
близких к
,
близких к
 (ошибка
(ошибка
 )
)
Доказать, что
Формула
Макларена:
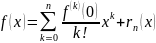
Теорема о единственности. Представление функции с помощью многочлена Тейлора единственно.
От противного.
Если
исходная функция имеет в точке
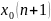 производную (все элементарные функции
дифференцируемы на области определения
сколь угодно раз), причем
производную (все элементарные функции
дифференцируемы на области определения
сколь угодно раз), причем
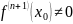 ,
тогда
,
тогда

Основные формулы представления элементарных функций по формуле Тейлора-Макларена.
Разложение геометрической прогрессии.
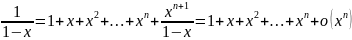
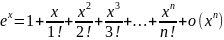
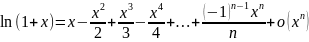
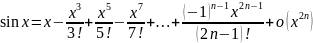

Биноминальное разложение
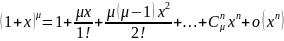
Глобальная теорема Тейлора. Формула Тейлора на отрезке.
Теорема. (Глобальная теорема Тейлора) Если функция на отрезке удовлетворяет следующим условиям:
 имеет
непрерывных производных на отрезке.
имеет
непрерывных производных на отрезке.Существует конечная
 .
.
Тогда
 справедлива формула:
,
где
справедлива формула:
,
где
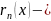 остаточный
член в формуле Тейлора на отрезке,
который в форме Лагранжа записывается
в виде
остаточный
член в формуле Тейлора на отрезке,
который в форме Лагранжа записывается
в виде
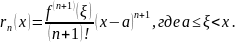
Аналогичная
теорема справедлива для отрезка
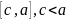 .
.
Рассматриваем 2 функции, удовлетворяющие условиям теоремы Коши:
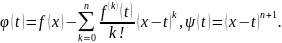
Оценка остаточного члена. Вычисление функции на отрезке с помощью формулы Тейлора.
Теорема.
Если
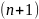 -я
производная ограничена на интервале
,
т.е.
-я
производная ограничена на интервале
,
т.е.
 такая, что
такая, что
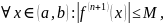 тогда
тогда

Оценка модуля остаточного члена.
Кроме формы Лагранжа существуют другие формы записи остаточного члена (формы Коши, Милна и т.д.)
Форма
по Коши:

Исследование функций с помощью производных.
Критерий монотонности функции на интервале.
Теорема.
Для того, чтобы дифференцируемая функция
на интервале
была монотонной (убывающей или
возрастающей), необходимо и достаточно,
чтобы
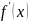 на интервале
была неотрицательной или неположительной,
причем, если
на интервале
была неотрицательной или неположительной,
причем, если
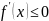 ,
то функция монотонно убывает на
,
если
,
то функция монотонно убывает на
,
если
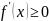 ,
то функция монотонно возрастает.
,
то функция монотонно возрастает.
По теореме Лагранжа, перемена знака.
Теорема верна и в том случае, когда функция непрерывна, но не имеет производную в конечном числе точек
Если на
на
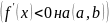 ,
то функция на этом интервале строго
монотонна, однако строгие неравенства
не гарантируют необходимых и достаточных
условий для монотонности.
,
то функция на этом интервале строго
монотонна, однако строгие неравенства
не гарантируют необходимых и достаточных
условий для монотонности.