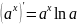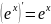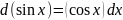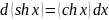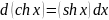Основные формулы дифференцирования элементарных функций.

Производная	Дифференциал

Дифференцирование показательно-степенных выражений:

– продифференцировать как показательную функцию, а потом как степенную и результаты дифференцирования сложить.

Кривые на плоскости и функции, заданные параметрически. Дифференцирование параметрически заданных функции.

Опр. Кривой на плоскости xoy называют всякий образ отрезка при непрерывном отображении .

параметрическое задание кривых (параметризация).

Функции 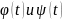– непрерывные функции параметра .

Непрерывность отображения означает, что оно либо растягивает, либо сжимает участки , искривляет и помещает в , но не разрывает отрезок .

При параметризации задается начало конец и направление движения вдоль кривой, таким образом параметрическое задание удобно для описания траектории движения материальной точке.

Одну и ту же кривую на плоскости можно задать бесконечным множеством параметризаций.

Опр. . Кривые, заданные параметрически, эквивалентны, если существует отображение непрерывное и строго монотонное такое, что диаграмма коммутативна, т.е. .

Опр. Пусть дана параметризация прямой на плоскость. Эта параметризация называется непрерывно дифференцируемой, если функции на отрезке дифференцируемы и имеют непрерывные производные.

В том случае, когда параметризация строго монотонная у нее существует обратная функция , в этом случае параметризация задает не только кривую, но и функцию, при этом существование обратной функции не означает, что мы сможем практически разрешить это уравнение относительно t, аналогично, если строго монотонна .

Дифференцирование параметрически заданных функций.

Правило. Если имеется функция, заданная параметрически, то необходимо продифференцировать по t оба уравнения и поделить функцию , при этом производная функции запишется в параметрическом виде следующим образом:

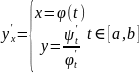
Если функция задана параметрически, то и производная должна быть задана параметрически. В таком виде производная 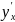готова к новому дифференцированию.

Уравнение касательной прямой, в кривой, заданной параметрически.

3 Класса точек параметрически заданной кривой:

1. 

– в точках I класса обязательно существует касательная, которая записывается симметричным уравнением.

2. 

Уравнение может быть записано и в виде уравнения для I класса.

3. 

В данном случае не гарантированно, что функция запишется в виде .

Такие точки в дальнейшем будем называть особыми точками параметрически заданной функции. В них одновременно обе производные равны 0.

Оказывается, в особых точках касательная прямая может быть, а может ее и не быть вовсе, это определяется старшими производными в точке и является предметом изучения такой науки как дифференциальная геометрия.

Вывод. В неособой точке параметрически заданной кривой обязательно существует касательная и она записывается уравнением .

Нормальная прямая в точке кривой, заданной на плоскости.

Опр. Прямую N, проходящую через 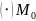кривой и перпендикулярную касательной прямой, называют нормальной прямой к кривой Г в .

– уравнения нормали в