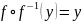- •Свойства модуля:
- •Числовая последовательность
- •Предел числовой последовательности
- •Свойства сходящихся последовательностей:
- •Верхний и нижний пределы последовательности.
- •Точки сгущения (предельные точки).
- •Определение предела функции по Гейне и Коши
- •Дифференцируемость функции в точке. Дифференциал функции. Его геометрический и физический смыслы.
- •Основные формулы дифференцирования элементарных функций.
- •Уравнение касательной прямой, в кривой, заданной параметрически.
- •3 Класса точек параметрически заданной кривой:
- •Гладкие функции и гладкие кривые на плоскости.
- •Старшие производные и дифференциалы функций.
- •Производные и дифференциалы старших порядков для сложных функций.
- •Теоремы о среднем для дифференцируемых функций.
- •Вычисление пределов с помощью правил Лопиталя.
- •Исследование локальных экстремумов функции.
- •Нахождение глобального экстремума функции на отрезке.
- •Асимптоты функции. Горизонтальные, вертикальные, наклонные.
Верхний и нижний пределы последовательности.
Из
теоремы Б-В и замечания к ней следует,
что из
можно выделить либо сходящуюся, либо
б.б.п.
Опр. Предел какой-либо подпоследовательности данной последовательности называется частичным пределом этой последовательности.
 – множество
частичных пределов
– множество
частичных пределов

Опр.
Наибольший из пределов, принадлежащих
,
– верхний предел (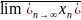
Опр.
Наименьший из пределов, принадлежащих
,
– нижний предел (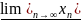
Определение
нижнего и верхнего пределов подразумевает
пространство
 .
.
Теорема. (О существовании верхнего и нижнего пределов) В любая последовательность имеет свой верхний и нижний пределы.
Нижний: 1 – неограниченна снизу (по Б-В: )
2 – ограниченная снизу
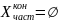 (по Б-В:
)
(по Б-В:
)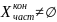 (
(
Теорема.
(Критерий №3 сходимости числовой
последовательности) Для того, чтобы
последовательность
сходилась необходимо и достаточно,
чтобы
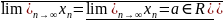
Необходимость:

Достаточность: по определению (за пределами окрестности содержится с каждой стороны конечное число членов, иначе можно было бы выделить подпоследовательности с пределами, не равными a).
Точки сгущения (предельные точки).
Опр. Точка называется предельной точкой множества Х, если
 ;
в противном случае, а
– изолированная
точка множества Х.
;
в противном случае, а
– изолированная
точка множества Х.
Из определения точки сгущения следует, что в любой окрестности точки сгущения содержится бесконечное множество членов данного множества.
Основное свойство предельной точки (точки сгущения).
Лемма. Х – числовое множество, точка а – точка сгущения множества (предельная точка):
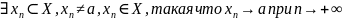
Выбираем нестационарную последовательность, уменьшая вдвое окрестность точки а, из которой берем очередной элемент.
– единственная
точка сгущения множества
.
Именно поэтому предел последовательности
находится только при
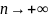 (n
стремится к точке сгущения).
(n
стремится к точке сгущения).
Определение предела функции по Гейне и Коши
– произвольная функция, Х – область определения
 – точка
сгущения множества Х, т.о.
точка а не обязательно является элементом
множества Х (f(x)
не обязательно определена в точке а,
значения f(a)
может не существовать)
– точка
сгущения множества Х, т.о.
точка а не обязательно является элементом
множества Х (f(x)
не обязательно определена в точке а,
значения f(a)
может не существовать)
Опр.
(по Гейне – на языке последовательностей)
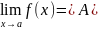 ,
если
,
если
 соответствующая
последовательность значений f(x)
{f(
соответствующая
последовательность значений f(x)
{f(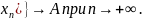
Если предел у функции существует, то он единственен
Многие свойства пределов последовательностей переносятся на пределы функции
Значение предела не зависит от того, определена ли функция в точке
Иметь предел в точке – это локальное свойство функции, т.е. свойство, зависящее от малой окрестности точки a.
Отрицание предела по Гейне.
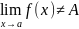 ,
если
,
если

 .
.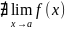 ,
если
,
если
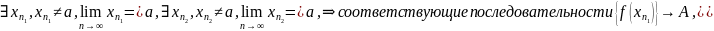 .
.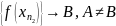 .
.
Опр.
(по Коши – на языке
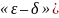
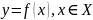
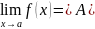 ,
если
,
если
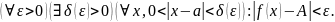
Окрестность
около а берется с выколотой точкой
(проколотая окрестность
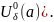
Опр.
(на языке окрестностей)
,
если
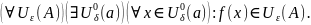
Отрицание предела по Коши.
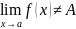 ,
если
,
если

, если

Односторонние пределы функции.
Теорема.
Пусть при
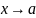 существуют конечные односторонние
пределы, которые равны между собой,
тогда существует предел функции в этой
точке, равный их общему значению.
существуют конечные односторонние
пределы, которые равны между собой,
тогда существует предел функции в этой
точке, равный их общему значению.
По определению
Арифметические свойства предела функции в точке.
 ,
,

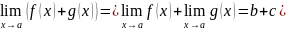
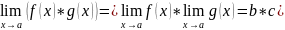
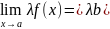
 ,
если
,
если

Бесконечно малые функции
Опр.
Функция f(x)
при
называется бесконечно малой, если
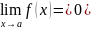
Теорема.
Для того, чтобы функция имела конечный
предел b
необходимо и достаточно, чтобы
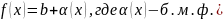
По определению (Коши)
Сравнение б.м.ф
 ,
,
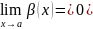
Опр.
2 б.м.ф.
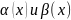 при
называются эквивалентными бесконечно
малыми, если
при
называются эквивалентными бесконечно
малыми, если

Опр.
Б.м.ф. называется бесконечно малой высшего
порядка, чем б.м.ф.
называется бесконечно малой высшего
порядка, чем б.м.ф.
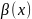 ,
если
,
если


Опр.
Если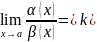
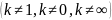
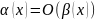 – бесконечно
малые одного порядка
– бесконечно
малые одного порядка
Второй замечательный предел.
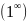
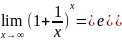
Любое
действительное число заключено между
двумя натуральными (для
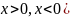
Первый замечательный предел.
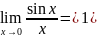
Сравнение
площадей равнобедренного треугольника,
сектора и прямоугольного треугольника,
определение по Коши:
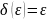 .
.
Критерий Коши для функции
Теорема.
(Критерий Коши для функции) Для того,
чтобы
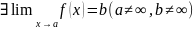 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
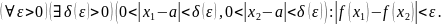
Необходимость (достаточность): определение предела по Коши (Гейне)
Непрерывные функции
Опр. Функция называется непрерывной в точке , если (3 определения непрерывности функции в точке)
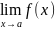 существует
и равен значению функции в этой точке
существует
и равен значению функции в этой точке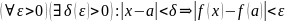
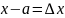 – приращение
аргумента в точке
,
– приращение
аргумента в точке
,
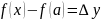 – приращение функции.
– приращение функции.
Функция называется непрерывной в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
Непрерывность,
по существу, замена пределов:

Утв. Арифметические действия не выводят из класса непрерывных функций.
f(x),
g(x)
непрерывные функции в точке

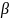
Из свойств предела функции в точке
Непрерывность сложной функции
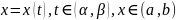
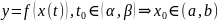
Теорема.
Пусть функция
 непрерывна в точке
непрерывна в точке
 ,
функция
,
функция
 непрерывна в точке
непрерывна в точке
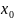 ,
тогда сложная функция непрерывна в
точке
.
,
тогда сложная функция непрерывна в
точке
.
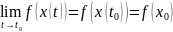
По определению предела функции по Коши
Непрерывность обратной функции
Теорема.
Пусть
монотонна и непрерывна на
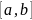 ,
тогда на
,
тогда на
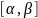 ,
где
,
где
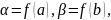 существует обратная функция
существует обратная функция
 которая непрерывна для
которая непрерывна для
 .
.
Лемма
1
 непрерывна и монотонная на
.
непрерывна и монотонная на
.
 ,
,
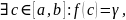 т.е. значения
сплошь заполняют отрезок
.
т.е. значения
сплошь заполняют отрезок
.
с – внутренняя точка отрезка; выбираем 2 последовательности
Лемма 2 Пусть монотонная на и ее значения сплошь заполняют , тогда непрерывна на .
От
противного (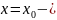 точка разрыва, двусторонние пределы)
точка разрыва, двусторонние пределы)
По Лемме 1 - значения сплошь заполняют отрезок, доказать монотонность, по Лемме 2 – непрерывность.
Классификация точек разрыва
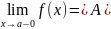 ,
,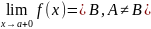 – разрыв I
рода типа конечного скачка
– разрыв I
рода типа конечного скачка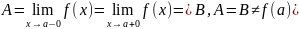 – разрыв
I
рода устранимый
– разрыв
I
рода устранимый −
разрывы
II
рода (среди них выделяют разрывы типа
бесконечного скачка)
−
разрывы
II
рода (среди них выделяют разрывы типа
бесконечного скачка)
Свойства непрерывных функций. Обратная функция.
Биективные отображения
На
декартовой плоскости графики прямой
и обратной функции совпадают. Но если
записать
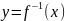 ,
то они симметричны относительно
биссектрисы координатного угла.
,
то они симметричны относительно
биссектрисы координатного угла.
Тождества:
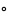 – суперпозиция
– суперпозиция
Точки разрыва функции ищутся только среди точек сгущения области определения функции, т.е. либо в Х, либо на границе.
Свойства функций, заданных на множествах.
Теорема Вейерштрасса. Теорема Больцано-Коши.
Опр. Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
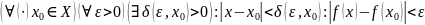
Утв. Все элементарные функции непрерывны в области определения
Графиком непрерывной функции является кривая линия, или «нить».
 :
f(x)
непрерывна на Х
:
f(x)
непрерывна на Х
Теорема.
(Вейерштрасса) Если
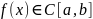 ,
то f(x)
ограничена на этом отрезке и достигает
на нем своих точных граней.
,
то f(x)
ограничена на этом отрезке и достигает
на нем своих точных граней.
По определению точных граней, с выбором последовательности и подпоследовательности.
Если
,
то
 отрезок
отображается в отрезок.
отрезок
отображается в отрезок.
Теорема. (Больцано-Коши – о промежуточном значении непрерывной функции)
Если
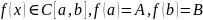 ,
то
,
то
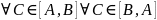 :
:
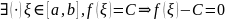
Существует
по крайней мере одна точка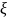 ,
их может быть и больше.
,
их может быть и больше.
Для
 (в противном случае аналогично). Пошагово
делим отрезок на 2 равные части, выбирая
ту, в которой содержится значение С.
Получаем стягивающуюся систему вложенных
отрезков, теорема о 2х милиционерах.
(в противном случае аналогично). Пошагово
делим отрезок на 2 равные части, выбирая
ту, в которой содержится значение С.
Получаем стягивающуюся систему вложенных
отрезков, теорема о 2х милиционерах.
Следствие.
Если непрерывная функция на концах
отрезка принимает значения А и В разных
знаков, то на исходном отрезке
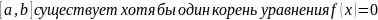 .
.
Замечательные следствия второго замечательного предела и непрерывности функции.
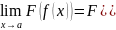
Знак предела и знак непрерывной функции переставимы.
Следствия II замечательного предела
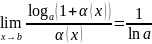 ,
если
,
если
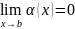
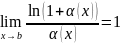 ,
если
,
если
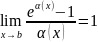 ,
если
,
если
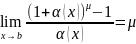 ,
если
,
если

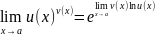
Равномерно непрерывные функции на множестве. Теорема Кантора о равномерно непрерывной на отрезке функции.
Опр.
Функция называется равномерно непрерывной
на множестве Х (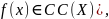 если
если

Опр.
 если
если
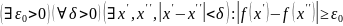
Произведение 2х равномерно непрерывных функций не является равномерно непрерывной функцией.
Теорема.
(Кантора)
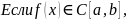
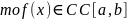
От противного (последовательности, из второй выделить подпоследовательность , стремящуюся к )
Следствие из теоремы Кантора и теоремы о равномерной непрерывности.
Если
 ,
то для любого
отрезок
,
то для любого
отрезок
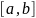 можно разбить на отрезки
можно разбить на отрезки
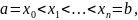 максимальная
длина которых не превосходит
максимальная
длина которых не превосходит
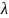 ,
что колебание функции на каждом отрезке
не превосходит
.
,
что колебание функции на каждом отрезке
не превосходит
.
Дифференциальное исчисление функции одной переменной.
Задачи, приводящие к понятию производной:
О мгновенной скорости движущейся материальной точки
О линейной плотности неоднородного линейного стержня
Понятие производной функции.
Опр.
Пусть задана произвольная функция
 .
Функция имеет в точке
производную, если существует конечный
предел
.
Функция имеет в точке
производную, если существует конечный
предел
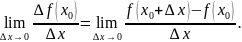
Если производная у функции существует в точке, то физический смысл ее есть мгновенная скорость изменения процесса в данной точке.
Обозначение
производной
 .
.
Понятие производной можно обобщить.
Опр.
У функции
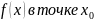 существует обобщенная производная,
равная
или
(предел определенного знака), если
существует обобщенный предел
существует обобщенная производная,
равная
или
(предел определенного знака), если
существует обобщенный предел
 .
.
Если предел равен бесконечности неопределенного знака, то производная функции в точке не существует, так же как если бы предел вообще не существовал.
Если
функция
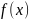 определена в односторонней окрестности
точки
:
определена в односторонней окрестности
точки
:
Правая производная функции:

Левая производная функции:
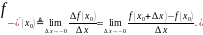
Односторонние производные бесконечны, если односторонние пределы есть бесконечность определенного знака.
Теорема.
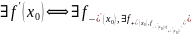

Доказательство из теоремы о связи односторонних пределов с двухсторонними.
Теорема верна и в случае конечной производной, и в случае бесконечной производной определенного знака
Геометрический смысл производной функции в точке.
Уравнение касательной прямой к графику функции в точке.
- на плоскости хоу задана некоторая прямая в окрестности точки .
L – секущая прямая.
 ,
где
,
где
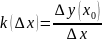
Опр.
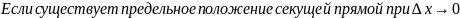 ,
то у графика функции в точке
существует касательная прямая.
,
то у графика функции в точке
существует касательная прямая.
Геометрический смысл производной функции в точке есть угловой коэффициент касательной прямой (тангенс угла наклона касательной)..

У функции существует касательная прямая в точке, если:
У функции в точке существует конечная производная
У функции в точке существует производная в обобщенном смысле
У функции в точке не существует и
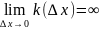 (бесконечность неопределенного знака).
(бесконечность неопределенного знака).
Если
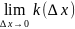 не
существует, то и касательная к графику
функции в точке не существует.
не
существует, то и касательная к графику
функции в точке не существует.