
- •Свойства модуля:
- •Числовая последовательность
- •Предел числовой последовательности
- •Свойства сходящихся последовательностей:
- •Верхний и нижний пределы последовательности.
- •Точки сгущения (предельные точки).
- •Определение предела функции по Гейне и Коши
- •Дифференцируемость функции в точке. Дифференциал функции. Его геометрический и физический смыслы.
- •Основные формулы дифференцирования элементарных функций.
- •Уравнение касательной прямой, в кривой, заданной параметрически.
- •3 Класса точек параметрически заданной кривой:
- •Гладкие функции и гладкие кривые на плоскости.
- •Старшие производные и дифференциалы функций.
- •Производные и дифференциалы старших порядков для сложных функций.
- •Теоремы о среднем для дифференцируемых функций.
- •Вычисление пределов с помощью правил Лопиталя.
- •Исследование локальных экстремумов функции.
- •Нахождение глобального экстремума функции на отрезке.
- •Асимптоты функции. Горизонтальные, вертикальные, наклонные.
Числовая последовательность
Опр. Всякую функцию натурального аргумента (всякое отображение множества натуральных чисел в множество действительных чисел) называют числовой последовательностью
Числовая
последовательность – бесконечный
набор действительных чисел
 …
Эта последовательность является
упорядоченным множеством, Порядок в
последовательности наследуется из
…
Эта последовательность является
упорядоченным множеством, Порядок в
последовательности наследуется из
 .
.
n – номер числовой последовательности
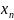 – n-й
член последовательности
– n-й
член последовательности
Обозначение:
{ ,
,

Интерпретации числовой последовательности:
«Механическая»: Если задана последовательность { ,
 ,то
на действительной числовой прямой
изображение точки в n-е
моменты совершает прыжок из точки
,то
на действительной числовой прямой
изображение точки в n-е
моменты совершает прыжок из точки
 .
Начальное положение в точке
.
Начальное положение в точке
 .
.Геометрическая: Если задана последовательность { задана функция
 График
последовательности - бесконечный набор
точек – невыразителен, поэтому точки
соединяют.
График
последовательности - бесконечный набор
точек – невыразителен, поэтому точки
соединяют.
Предел числовой последовательности
Опр.
Числовая последовательность
называется сходящейся к числу
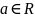 (имеет предел, равный а:
(имеет предел, равный а:
 ),
если
),
если
 .
.
В противном случае последовательность расходящаяся – не имеет предела:

Интерпретация: последовательность имеет предел в точке а, значит изображение точки, прыгая вдоль оси, в конкретный момент времени попадет в окрестность точки а и больше не выйдет из этой окрестности. Если изменить , то изменится и момент времени.
Внутри окрестности находится бесконечное множество членов последовательности, а за пределами – конечное число членов.
Опр.
(на
языке окрестностей)
,
если

Свойства сходящихся последовательностей:
Корректность определения предела
Теорема. Если последовательность имеет предел, то он единственен, либо последовательность не имеет предела вообще.
От
противного (
,

По определению
Сходящая числовая последовательность является ограниченным числовым множеством.
По определению
Обратное утверждение неверно. Если последовательность ограничена, это не значит, что она сходящаяся.
Лемма о двух милиционерах
Пусть
имеется 3 числовые последовательности,
для которых выполняется неравенство
 ,
начиная с
или
,
начиная с
или
 , тогда, если
,
, тогда, если
, ,
то и
,
то и
 .
.
По определению

 – произвольные
последовательности, начиная с
– произвольные
последовательности, начиная с

 ,
тогда, если
,
тогда, если

В пределе сохраняется нестрогое неравенство
От противного
Следствия:
1.

2.



По определению
Знак
модуля и знак предела перестановочны
друг с другом (можно выносить
 и наоборот)
и наоборот)
 (вспомогательное)
Если
(вспомогательное)
Если
 ,
,

Бесконечно малые последовательности (величины)
Опр. Последовательность называется бесконечно малой, если предел этой последовательности равен нулю.
Теорема.
(Критерий №1) Для того, чтобы
последовательность
была сходящейся необходимо и достаточно,
чтобы члены последовательности
записывались в виде
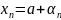 ,
где
,
где

По определению
Бесконечно большие последовательности (величины)
Опр.
Все последовательности
,
сходящиеся к
 ,
–- это бесконечно большие последовательности.
,
–- это бесконечно большие последовательности.
 ,
если
,
если

 ,
если
,
если

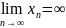 ,
если
,
если

Б.б.п не существуют в природе. Это вводится для удобства описания процессов, поэтому б.б.п остаются расходящимися.
Свойства пределов последовательностей, связанные с арифметическими операциями
1.
2.

3. ,
где
,
где
 (может выполняться с некоторого номера)
(может выполняться с некоторого номера)
 Алгебраическая
сумма двух б.м.п. есть б.м.п.
Алгебраическая
сумма двух б.м.п. есть б.м.п.
По определению
Следствие. Сумма конечного числа б.м.в. есть б.м.в.
Сумма бесконечного числа б.м.в. не обязательно является величиной бесконечной малой.
 Произведение
б.м.в. на ограниченную величину есть
б.м.в.
Произведение
б.м.в. на ограниченную величину есть
б.м.в.
По определению
Следствие. Произведение конечного числа б.м.в. есть б.м.в.
 Теорема.
Если
Теорема.
Если
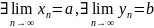 ,
тогда
,
тогда


Если
 ,
тогда
,
тогда

Расписать через бесконечно малые
Арифметические свойства справедливы только, если пределы последовательностей существуют, если пределы не существуют или последовательности расходятся, то арифметические свойства становятся несправедливыми.
Монотонные числовые последовательности.
Предел монотонной последовательности.
Поскольку числовые последовательности есть числовые множества, то переформулируем данные ранее определения точных граней для последовательностей.
Опр.

Опр.

Опр.
Последовательность
называется строго убывающей, если

Опр.
Последовательность
называется невозрастающей, если

Опр.
Последовательность
называется строго возрастающей, если

Опр.
Последовательность
называется неубывающей, если

Теорема. (О монотонной последовательности)
Если
 (строго или нестрого) и ограничена
сверху, то у нее существует предел,
равный
(строго или нестрого) и ограничена
сверху, то у нее существует предел,
равный
 (
(
 .
.Если
 (строго или нестрого) и ограничена
снизу, то
(строго или нестрого) и ограничена
снизу, то
 .
.Если монотонна и неограниченна, то ее предел равен , если
 и
и
 ,
если
,
если

По определениям предела и точных граней.
Следствие. Если монотонна и ограничена, то она обязательно имеет предел. Критерий сходимости монотонной последовательности.

Число
 .
.


Доказательство
существования предела: монотонность
(Бином Ньютона) и ограниченность
(отбросить скобки, заменить соответственно
n!
на
 ).
).
Метод Ньютона (касательных) отыскания корней уравнения
 – уравнение
касательной
– уравнение
касательной

Вычисление приближенного значения функции – предел образовавшейся последовательности.
Метод вложенных отрезков. Теорема Кантора.
Опр.
Систему отрезков
 называют вложенной системой отрезков,
если концы отрезков удовлетворяют
неравенству
называют вложенной системой отрезков,
если концы отрезков удовлетворяют
неравенству

Опр.
Система отрезков
называется стягивающейся, если
последовательность

Опр. Если система отрезков и вложенная и стягивающаяся, то ее называют стягивающейся системой вложенных отрезков.
Теорема.
(Кантора) Если система отрезков
- стягивающаяся система вложенных
отрезков, то
 ,
принадлежащая всем отрезкам одновременно.
,
принадлежащая всем отрезкам одновременно.
Последовательности
концов отрезков – монотонные, ограниченные
(
Подпоследовательности данной последовательности (частичные последовательности).
Теорема Больцано-Вейерштрасса.
Опр.
Пусть даны 2 числовые последовательности
 .
Последовательность
.
Последовательность
 является подпоследовательностью
последовательности
является подпоследовательностью
последовательности
 (частичной последовательностью), если
(частичной последовательностью), если
 – каждый
член подпоследовательности
является некоторым членом последовательности
.
– каждый
член подпоследовательности
является некоторым членом последовательности
. – порядок
членов подпоследовательности сохраняется
(наследуется) порядком членов
последовательности.
– порядок
членов подпоследовательности сохраняется
(наследуется) порядком членов
последовательности.
Лемма
Если последовательность
сходится,

 ,
то любая подпоследовательность сходится
к a
(
,
то любая подпоследовательность сходится
к a
( ).
).
По определению предела
Теорема. (Больцано-Вейерштрасса) Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Методом «ловли льва в пустыне». Деление отрезка пополам с выбором отрезка с бесконечным количеством членов – получаем стягивающуюся систему вложенных отрезков.
Если
последовательность
неограниченна сверху (снизу) , то,
используя обобщенные понятия предела,
из нее можно выделить подпоследовательность
бесконечно большую, сходящуюся к
 (доказывается
аналогично).
(доказывается
аналогично).
Используя
обобщенные числа
 любая последовательность имеет
сходящуюся подпоследовательность в
обобщенном смысле.
любая последовательность имеет
сходящуюся подпоследовательность в
обобщенном смысле.
Фундаментальные последовательности (сходящиеся в себе).
Критерий Коши. Полнота числовой прямой .

Опр.
– фундаментальная (сходящаяся в себе),
если

 (условие
Коши фундаментальности последовательности)
(условие
Коши фундаментальности последовательности)
Лемма. Если – фундаментальна, то – ограниченная последовательность, как числовое множество.
По определению
при
 (вне
(вне
 находится конечное число членов)
находится конечное число членов)
Теорема (Критерий Коши о сходимости числовой последовательности №2) Для того, чтобы последовательность сходилось в необходимо и достаточно, чтобы была фундаментальной.
Необходимость: по определению (расписать модули)
Достаточность: ограниченность, теорема Больцано-Вейерштрасса, условие Коши фундаментальности последовательности.
Отрицание критерия Коши: расходится в не является фундаментальной, т.е.

Последовательность
 при
при
 сходится, при
сходится, при
 расходится.
расходится.
Критерий Коши называется свойством полноты числовой прямой: из сходимости в себе следует сходимость в пространстве . В функциональном анализе это свойство взято за основу определения полного пространства.




