5 Відношення еквівалентності, порядку, толерантності

Розглянемо деякі найчастіше використовувані класи бінарних відношень.

Бінарне відношення, що має властивість рефлективності, симетричності і транзитивності, називається відношенням еквівалентності (позначається ).

Нехай задана множина А і відношення еквівалентності, що визначене на цій множині: RAA. Елементи а і bA, для яких виконується aRb, називаються еквівалентними.

Приклад. Відношення «=» на множині чисел є відношення еквівалентності. Відношення «Вчаться в одній групі» також відношення еквівалентності на множині студентів всього технікуму. Відношення «мають однакові імена» на множині людей є відношення еквівалентності.

Важлива властивість будь-якого відношення еквівалентності, що визначене на множині А, полягає в тому, що воно розбиває множину А на неперетинні підмножини, які називаються класами еквівалентності. У випадку скінченної множини А розбиття її на класи відбувається таким чином. Нехай на множині А визначене відношення еквівалентності R. Виберемо елемент а₁ і утворимо клас С₁ елементів уА для яких існує а₁Rу. Клас С₁ може складатися також з одного елементу а₁. Якщо А≠ С₁, то виберемо елемент а₂, який не входе до С₁ і утворює клас С₂ елементів уА\С₁, для яких існує а₂Rу. Будемо продовжувати побудову класів до тих пір, доки не залишиться жодного елементу, що не входить до виділених вже класів. Ця система класів називається системою класів еквівалентності і має такі властивості:

1. класи попарно не перетинаються;

2. будь-які елементи з одного класу еквіваленті;

3. будь-які два елементи з різних класів не еквіваленті.

Приклад. Компанія студентів складається з 6 особ, яку розглянемо як множину: A={Петров Саша, Суслов Ілля, Кротов Саша, Мирний Олег, Чалий Олег, Марков Саша}. Розглянемо відношення між ними «мають однакове ім’я». Візьмемо будь-який елемент множини, наприклад Кротов Саша. Особи, що мають однакові з ним імена утворюють клас С₁ ={Петров Саша, Кротов Саша, Марков Саша}. Множина елементів, що входять до множини А, але не входять до класу С₁ містить елементи {Суслов Ілля, Мирний Олег, Чалий Олег}. Виберемо з неї будь-який елемент, наприклад, Суслов Ілля. Елементи, що утворюють з ним клас С₂ і мають відношення «Мають однакове ім’я» більш не існують крім самого елементу Суслов Ілля. Тобто С₂ ={ Суслов Ілля}. Елементи що залишились утворюють третій клас С₃ ={ Мирний Олег, Чалий Олег}.

Відношення називається відношенням часткового порядку (позначається ), якщо воно рефлексивне (а а), антисиметричне (якщо а b, b a, то b= a), транзитивне (якщо а b, b с, то а с).

Я кщо на множині задане відношення часткового порядку, то ця множина називається частково упорядкованою. Існує спосіб зображення скінченної частково упорядкованої множини, який називається діаграмою Хассе. Кожен елемент позначають точкою і два елементи з’єднують стрілкою від а до b, якщо а b і не існує сА такого, що а с b.

Приклад. Розглянемо відношення включення множин для деякої фіксованої множини {a, b, c}.

Із властивості транзитивності п

a

b

c

d

e

f

ов’язане поняття шляху в графі.

Шлях в графі відношення з вершини а до вершини b – це послідовність дуг від а до b: (а, х₁), (х₁, х₂), (х₂, х₃), ….(х_n-1, b), n1, де n – число дуг, називається довжиною шляху.

Ч асто при зображенні графа відношення порядку виключають дуги, які можна побудувати, використовуючи властивість транзитивності, тобто, якщо на графі існує шлях з а до b, то дугу (а, b) не зображують.

Крім того, розташовують вершини так, щоб спрямованість всіх дуг була в одному напрямку.

Елементи а і b називаються порівнянними у відношенні часткового порядку R, якщо виконується хоча б одне з співвідношень aRb або bRa. Множина А, на якій задане відношення часткового порядку і для якої всілякі два елементи цієї множини порівнянні, називається лінійно упорядкованою або повністю упорядкованою.

Повністю упорядкована множина відрізняється від частково упорядкованої тим, що у частково упорядкованій множині А можуть бути присутні елементи, з яких можна складати непорівнянні пари.

П риклад. Множина N натуральних чисел повністю упорядкована відносно природної операції порівняння , яка істинна на деякій підмножині R пар (a, b) декартова квадрата N². будь-які два елементи a, bN порівнянні за R, оскільки хоч одна з нерівностей ab або ba істинна.

Відношення часткового порядку, що є рефлексивним, антисиметричним і транзитивним, називається також відношенням нестрогого порядку. На відміну від нього відношення строгого порядку (позначається <) визначається такими властивостями:

а) антирефлексивність (якщо a<b, то a≠b);

б) асиметричність (якщо a<b, то не правильно b < a);

в) транзитивність (якщо a<b і b<с , то a<с).

Таким чином, якщо у відношенні нестрогого порядку властивість анти симетричності замінити асиметричністю, то отримаємо відношення строгого порядку.

Відношення називається відношенням толерантності, якщо воно: а) рефлексивне, симетричне, анти транзитивне.

Толерантність зображує собою формальне уявлення інтуїтивного поняття схожості. Схожість двох об’єктів не залежить від того, в якому порядку вони порівнюються. В той же час якщо один об’єкт схожий на другий, а другий на третій, то це не означає, що перший схожий на третій.

Розглянемо відношення толерантності на прикладі популярної задачі «перетворення мухи на слона» як відношення схожості чотирибуквених слів, що відрізняються на одну букву: муха-мура-тура-тара-кара-каре-кафе-кафр-каюк-крюк-крок-срок-сток-стон-слон.

Запитання.

1. Дайте визначення відношення еквівалентності.

2. Яким чином відбувається розбиття множини на класи еквівалентності? Які елементи називаються еквівалентними?

3. Які властивості характерні для класів еквівалентності?

4. Наведіть приклади відношень еквівалентності та одержуваних при цьому класів еквівалентності.

5. Дайте визначення відношення часткового порядку. Як воно позначається? Наведіть приклад.

6. Що таке шлях у графі? Як поняття шляху застосовується для дослідження графів відносного порядку?

7. Яка множина називається лінійно упорядкованою? Що таке порівнянні і непорівнянні елементи?

8. Чим відрізняється відношення повного порядку від відношення часткового порядку? Дайте визначення відношення строгого порядку.

9. Дайте визначення відношення толерантності. Наведіть приклад.

 Завдання

1. Які з наборів підмножин множини А={1, 2, 3, 4, 5, 6}можуть бути розбиттями цієї множини на класи еквівалентності:

1. {1, 2}, {2, 3, 4}, {4, 5, 6};

2. {1, 3, 5}, {2, 4, 6};

3. {1}, {2, 3, 6}, {4, 5};

4. {1, 4, 5}, {2, 6};

2. Нехай R₁ i R₂ – відношення еквівалентності. Визначте, чи вони еквівалентні відношенням:

1. R₁  R₂;

2. R₁  R₂;

3. 

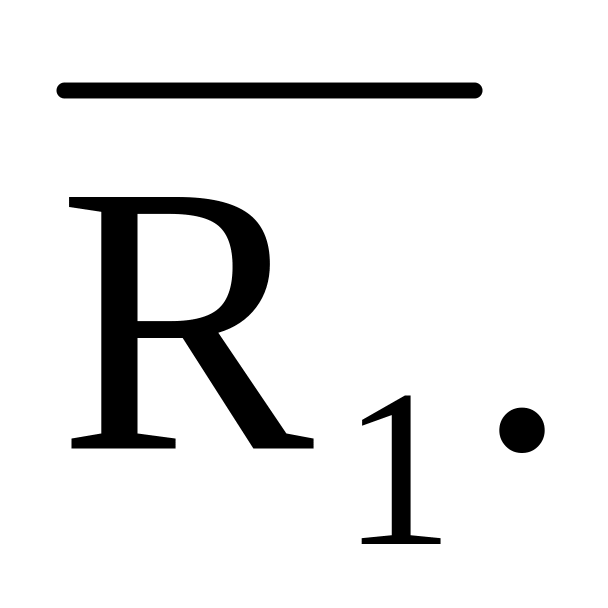
3. Нехай R₁ i R₂ – відношення часткового порядку. Визначте, чи є приведені відношення також відношеннями часткового порядку:

1. R₁  R₂;

2. R₁  R₂;