12. Определение тесноты связи между факторами: линейный коэффициент корреляции, коэффициент детерминации.

В качестве меры тесноты связи используется линейный коэффициент корреляции:

Где, и

Линейный коэффициент корреляции может принимать любые значения в пределах от минус 1 до плюс 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками.

Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак плюс, а обратной зависимости - знак минус.

Если сравнить формулы для расчета коэффициентов регрессии и корреляции, то можно увидеть, что между этими коэффициентами существует связь

Можно выразить коэффициент корреляции через

коэффициент регрессии:

Если b < 0 => -1 ≤ r < 0

Если b > 0 => 0 < r ≤ 1

r = 0 ==> связь между х и у отсутствует

0 <│r│≤ 0,3 => связь практически отсутствует

0,3 <│r│≤ 0,5 => слабая связь между х и у.

0,5 <│r│≤ 0,7 => средняя (умеренная связь).

0,7 <│r│< 1 => сильная связь.

│r│ =1 => функциональная связь.

d – коэффициент детерминации

Коэффициент детерминации показывает на сколько процентов изменение у обусловлено изменением х.

Оставшаяся доля приходится на влияние прочих факторов, не учтенных в модели.

13. Оценка тесноты связи в нелинейной регрессионной модели.

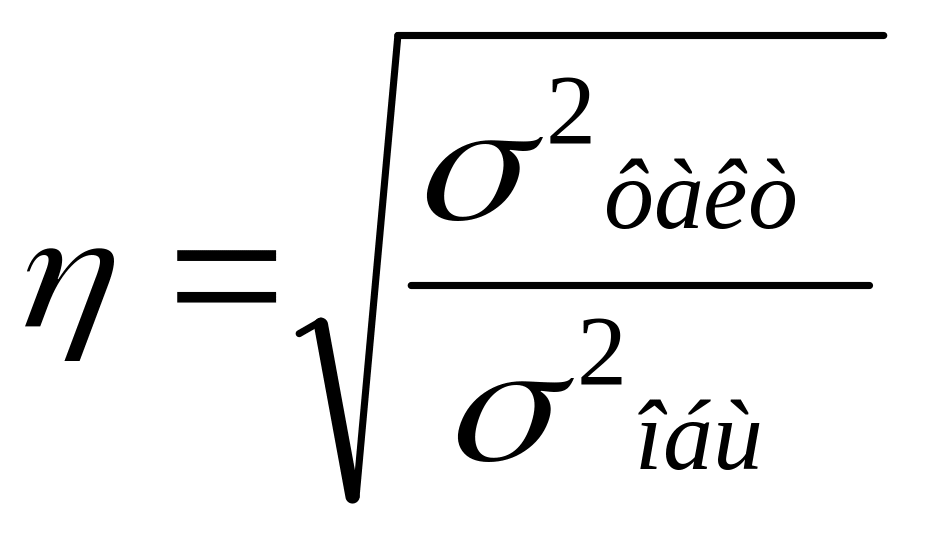
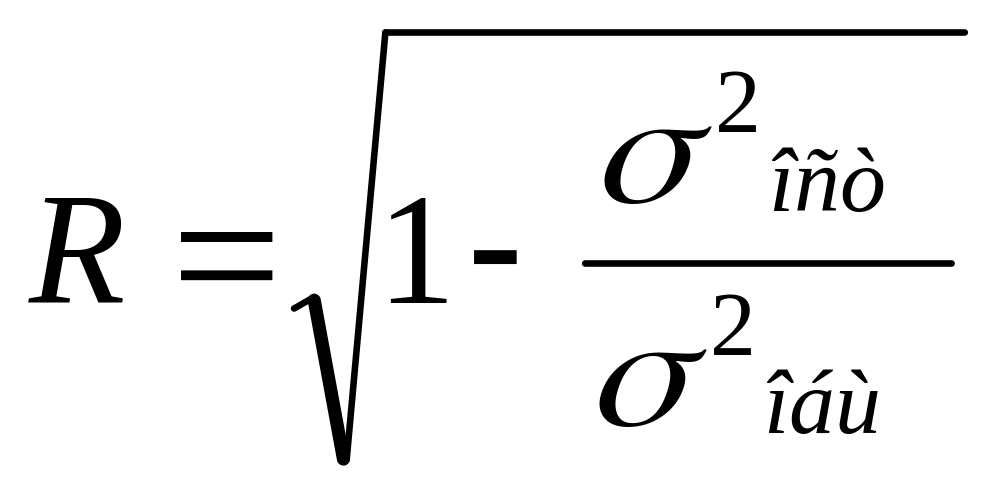
Коэффициенты корреляции должны быть подвергнуты оценке

статистической значимости.

n – объем выборки, m – число переменных при регрессии х.

Индекс детерминации:

- такой же смысл, как коэффициент детерминации в линейной модели.

И ндекс детерминации:

можно сравнивать с линейным коэффициентом детерминации

д ля объяснения возможности применения линейной функции. Чем больше кривизна линии регрессии, тем

Близость этих показателей означает, что можно использовать линейную функцию.

Н а практике пользуются таким правилом:

Если

то предположение о линейной связи считается оправданным.

В противном случае проводится оценка значимости различия между этими коэффициентами, вычисленными по одними и тем же данным.

В этом случае используется t-критерий Стъюдента.

различие существенны и замена нелинейной функции

линейной невозможна.

На практике пользуются правилом: если:

то различие считается несущественным и можно использовать линейную функцию даже если нелинейность обоснована эконометрически.

14. Оценка существенности параметров и статистическая проверка гипотез. T-критерий Стьюдента.

Для проверки статистических гипотез можно использовать следующую общую процедуру.

1) Выдвигается ноль-гипотеза о том, что коэффициент регрессии статистически незначим:

H₀:

или что уравнение в целом статистически незначимо:

H₀: ;

2) Определяется фактическое значение соответствующего критерия.

3) Сравнивается полученное фактическое значение с табличным.

4) Если фактическое значение используемого критерия превышает табличное, ноль-гипотеза отклоняется и с вероятностью (1-) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии или уравнения в целом. Если фактическое значение t-критерия (F-критерия) меньше табличного, то говорят, что нет оснований отклонять ноль-гипотезу.

Статистическая значимость коэффициента регрессии проверяется с помощью t-критерия Стьюдента. Для этого сначала необходимо определить остаточную сумму квадратов:

и ее среднее квадратическое отклонение:

Затем определяется стандартная ошибка коэффициента регрессии по формуле:

Фактическое значение t-критерия Стьюдента для коэффициента регрессии рассчитывается как:

()

Значение ( для 95% уровня значимости) позволяет сделать вывод об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) x и y. Малые значения t-статистики соответствуют отсутствию достоверной статистической связи между x и y.

Можно построить доверительный интервал для b. Из () имеем:

- 95% доверительный интервал для b.

Доверительный интервал накрывает истинное значение параметра b с заданной вероятностью (в данном случае 95%).