15. Основные характеристики распыленного потока атомов образца при облучении ионным пучком

. При ионном облучении обычно интерес представляет не сам траекторный пробег, а проективный (проецированный) пробег R_р, величина которого совпадает с проекцией траекторного пробега на первоначальное направление движения иона при входе в образец

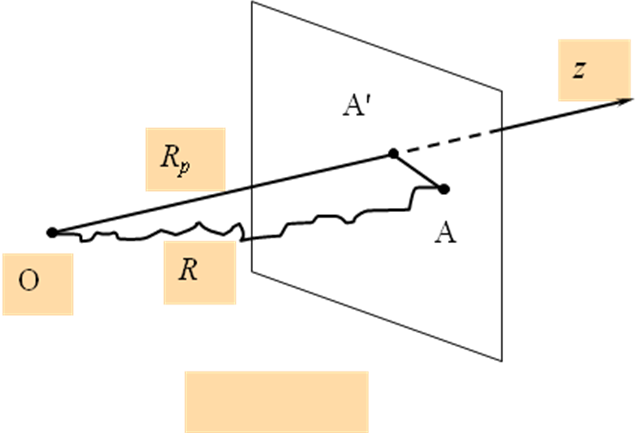
с реднее значение проективного пробега R_p,

– среднеквадратичное отклонение проективных пробегов

И нтегральной характеристикой, описывающей процесс отражения, является коэффициент отражения

где N_отр – все отраженные ионы с любыми энергиями и в любом зарядовом состоянии, вылетевшие из образца, облученного N₀⁺ ионами первичного пучка.

Отраженные ионы могут иметь разный зарядовый состав: однократно и многократно заряженные положительные и отрицательные ионы; нейтральные атомы, в том числе в возбужденном состоянии (снятие возбуждения осуществляется за счет высвечивания фотона видимого света). Характеристикой зарядового состояния является вероятность вылета в том или ином зарядовом состоянии (i) при данной энергии

16. Коэффициент распыления образца ионным пучком

Принято рассматривать два явления распыления – физическое и химическое.

Основной характеристикой процесса распыления является коэффициент распыления

Y = N_расп /N₀⁺,

где N₀⁺ – число ионов первичного пучка, попавших на образец за время облучения,

N_расп – число атомов, распыленных (выбитых) из образца в результате облучения.

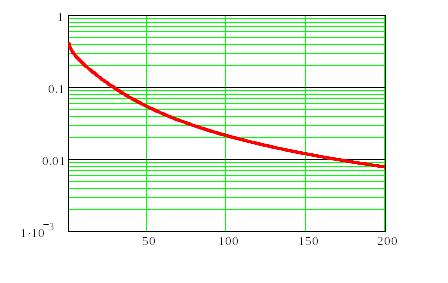
Коэффициент отражения ионов бора при имплантации в кремний

Расчет коэффициента распыления при облучении образца по нормали к поверхности в наиболее часто реализуемом режиме линейных каскадов может быть выполнен в рамках модели Зикмунда

1. Средний пробег иона в твердом теле от одного столкновения с атомом до другого Dl = n₀^1/3.

2. Столкновения иона происходят с каждым атомом М₂ по ходу движения иона, поэтому переданная атому энергия E₂ @ (dE/dl)_n = S_n(E)n₀ / n₀^1/3 = S_n(E)n₀^2/3.

3. Число выбитых из положения равновесия атомов в одном каскаде n_см = Е₂/2E_d.

4. Направление движения выбитых атомов – изотропно, поэтому к поверхности движется n_см /3 атомов

В этих предположениях

Если более точно учесть направление движения атомов в каскаде, зависящее от отношения масс f(М₂/М₁) и ввести E_s = E_d/2, то получится формула Зикмунда

В рамках данной модели расчет коэффициента распыления будет корректен для тяжелых ионов (Ar, Ne) и некорректен для ионов водорода и гелия, так как для этих ионов преобладают электронные потери, которые необходимо учесть.

Еще есть полуэмпирическая формула Матсунами.

Коэффициент распыления для любых пар ион/образец имеет максимум при энергии иона, которая соответствует максимальному значению ядерной тормозной способности для данной пары ион/образец.

Значения Y для большинства пар ион/образец 1¸5 (кроме М₁ ³ 100, когда реализуется режим нелинейных каскадов).

Для легких ионов (водород, гелий) Y ~ 10^-2¸ 10^-1.

Энергетический спектр распыленных атомов

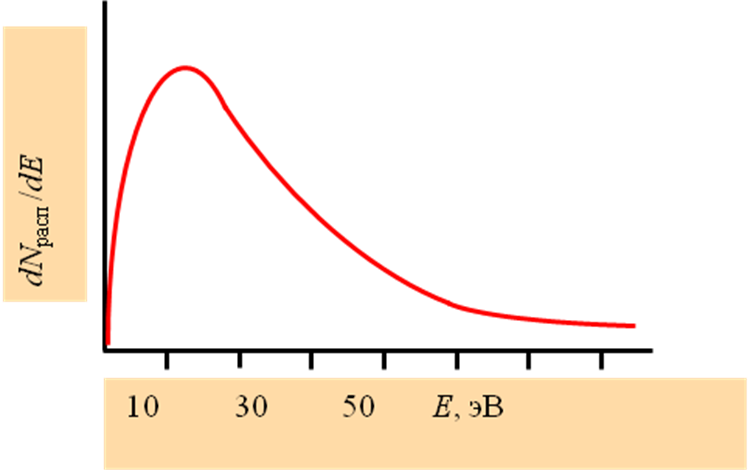
Энергетический спектр dN_расп /dE при облучении медного образца ионами аргона с энергией 10 кэВ.

В случае облучения образца по нормали к поверхности угловое распределение распыленных атомов примерно следует закону косинуса dN_расп/dW = N*cosa. Нормировочная константа N* определяется из следующего выражения

Угловое распределение распыленных атомов при бомбардировке образца по нормали к поверхности

В случае наклонного облучения образца, можно считать, что количество распыленных атомов пропорционально траектории бомбардирующего иона и выходят (распыляются) из образца лишь атомы, выбитые из положения равновесия на расстояниях от поверхности не больших d.

Тогда, если N_расп (0) – количество распыленных атомов при бомбардировке по нормали к поверхности, а N_расп (q) – количество распыленных атомов при бомбардировке под углом q к нормали, то N_расп (q)/N_расп (0) @ R₀/d = (d /cosq)/d = 1/cosq и, следовательно, коэффициент распыления при наклонной бомбардировке