1.Размер и форма земли.

1)Плоскость

-сис-ма плоских прямоугольных координат (х,у)

-подобие

-нет искажений(план)

2)Земля-шар(сфера)

5 в. До н.э.- Пифагор высказал предположение

4в до н.э. – Аристотель доказал

3в до н. э.- Эратосфен измерил размер земли ошибся на 2

- -карты

-искажения

цилиндрическая проекция

ортографическая(Апполоний)

ортографическая (Гепарх)

Фалес Милетский 6 в. До н.э. гномоническая проекция

Птолимей

Портоланы-морские карты

-не учитывали сферичность земли

-проведен линейный масштаб

1569-Герард Крамер (Меркатор) предложил равноугольную цилиндрическую

17вРоссия-появились мередианы и параллели

1701г Москва-Петр 1 организ. Московскую математ.- навигац. Школу

3)Двухосный эллипсоид вращения

1753 организ.2 экспедиции: север-Лапландия, юг-Перу

1 элипсоид- Деламбра

Клерка, Бессиля, Хейфорда, Красовского

Эллипсоиды различаются:

1.параметрами

А-большая полуось, α-сжатие, е-эксцентриситет

2.ориентировка в реальном теле земли, задается исходными геодезическими датами

-координаты начального пункта

-азимут на ориентирный пункт

-превышение геоида над эллипс. в начальном пункте

Элл-д Бальбека в 70-е 19в заменен на эл-д Бесселя

1940 –эл-д Красовского, ПЗ-90

Ламберт, Лагранж

Шуберт Ф. И. –работа о картограф. Проектирование эллипсоида

4) Трехосный эллипсоид

2.Геодезическая(геогр)сис-ма коорд.

Нормальные сечения:

1)мередианное

2)сечение одного вертикала

Широтой т.А называется угол между нормалью поверхности эллипсоида т.А и плоскостью экватора.

Долготой т.А называется двухгранный угол между меридианным сечением проходящим через т.А и меред. Сечением принятым за начальное.

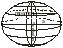
φ=-90^о

φ=const-параллель

r=Ncosφ

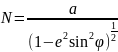
Меридиан- линия равных долгот

λ = const

1884г-решили считать долготы от Гринвича; о. Ферро(о. Иерро)

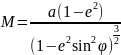
3.Полярная сферическая сис-ма координат.

Q-полис полярной сис-мы коорд.

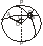z-зенитные расстояния

А-азимут

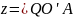
Z₀=0, z_экв=90^o

Z=const –альмукантарат

Зенитным расстоянием т.А называется угол между нормалью проведенной в точке нового полюса Q и направленного с т.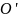 на т.А.

Азимут – это двугранный угол между 2-я нормальными сечениями, нормальным сечением и нормальным сечением принятым за начальное.

Азимут отсчет по часовой стрелке

а =const-вертикал

за начальный приним. Вертикал, кот. Одновременно является меридианом.

4. Связь между геодезической и полярной сферической системами координат.

t5 cosz=sinφsinφ_o+cosφcosφ_o+cos(λ-λ_o)

t4 sinzsinQ=cosφsin(λ-λ_o)

t1 sinzcosQ=sinφcosφ_o - cosφsinφ_ocos(λ-λ_o) 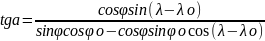-для сферы

cosz=t5+e²r(t5sinφ-sinφ_o)+…

sinz=t4(1+e²rsinφ)+…

sinzcosa=t1+e²τ(t1sinφ-cosφ_o)+…

τ= sinφ-sinφ_o

вывод: картографы пользуются след. Результатами геодезии:

1.параметрами эллипсоида

2. использ геодезич(географ) сис-му координат

3. значениями геодезич координ точек местности

Следует отметить-изменения в сис-ме координат приводит к изменению геодезич или географ координаты объекта.

Одна и та же точка в разных сис-ах координат будет иметь разные координаты.

Различия учитываются при проведении геодезических работ и создании карт крупных масштабов.

При созд карт меньше миллионного масс-ба разница не учитывается.