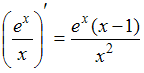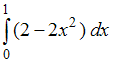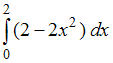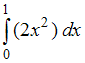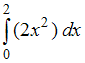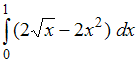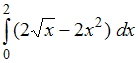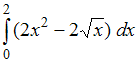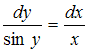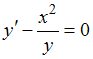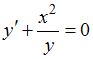- •Геометрические приложения определённого интеграла.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Числовые ряды.
- •Числовые характеристики случайных величин.
- •Алгоритмы на циклы с условием.
- •Решение:
- •Visual Basic – средство разработки программного обеспечения корпорации Microsoft, включающее язык программирования и среду разработки.
- •Решение:
- •Основные понятия программирования.
Д Е:
Математический анализ.
Е:
Математический анализ.
Понятие функции.
№1. Множество значений функции, график которой изображен на рисунке, имеет вид …
|
|
|
|
|
|
|
|
|
|
№2. Множество значений функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
Непрерывность функции. Точки разрыва.
№1. Бесконечное число точек разрыва имеет функция …
|
|
|
|
|
|
|
№2. В точке
![]() имеет
разрыв второго рода функция …
имеет
разрыв второго рода функция …
|
|
|
|
|
|
|
Дифференциальное исчисление. Формулы, основные правила дифференцирования.
№1. Производная функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
№2. Функция
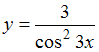 является
производной функции …
является
производной функции …
|
|
|
|
|
|
|
|
|
|
№3. Среди предложенных равенств неверным является …
|
|
|
|
|
|
|
|
|
|
Геометрические приложения определённого интеграла.
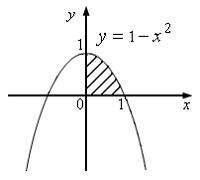
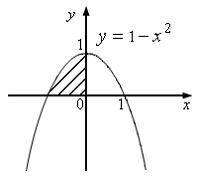
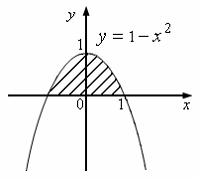
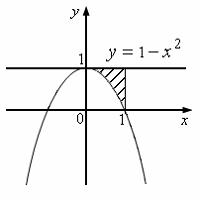
№1. Интеграл
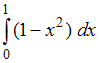 определяет
площадь фигуры, изображенной на рисунке …
определяет
площадь фигуры, изображенной на рисунке …
|
|
|
|
|
|
|
|
|
|
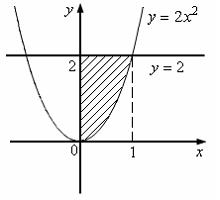
№2. Площадь фигуры, изображенной на
рисунке, определяется интегралом …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№3. Площадь фигуры, изображенной на
рисунке, определяется интегралом …
|
|
|
|
|
|
|
|
|
|
Дифференциальные уравнения с разделяющимися переменными.
№1. Переменные нельзя разделить в уравнении …
|
|
|
|
|
|
|
|
|
|
№2. Дифференциальное уравнение
![]() в
результате разделения переменных
сводится к уравнению …
в
результате разделения переменных
сводится к уравнению …
|
|
|
|
|
|
|
|
|
|
№3. Уравнение
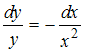 с
разделенными переменными можно получить
из уравнения …
с
разделенными переменными можно получить
из уравнения …
|
|
|
|
|
|
|
|
|
|
Числовые ряды.
№1. Установите соответствие между числовыми рядами и третьими членами этих рядов.
1.
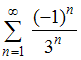 2.
2.
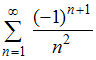 3.
3.

1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
№2. Установите соответствие между
числовыми рядами и частичными суммами
![]() этих
рядов.
этих
рядов.
1.
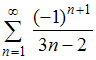 2.
2.
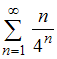 3.
3.
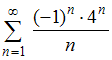
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
ДЕ: Теория вероятностей.
Элементы теории вероятностей. Математика случайного.
№1. В проведенных
![]() испытаниях
событие
испытаниях
событие
![]() появилось
40 раз. Установите соответствие между
количеством
проведенных
испытаний и относительной частотой
появилось
40 раз. Установите соответствие между
количеством
проведенных
испытаний и относительной частотой
![]() появления
события
появления
события
![]() .
1.
.
1.
![]() 2.
2.
![]() 3.
3.
![]()
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
№2. Относительная частота приобретения
нестандартной продукции при покупке
![]() банок
консервов оказалась равной
банок
консервов оказалась равной
![]() .
Установите соответствие между числом
купленных
банок и количеством банок качественных
консервов:
.
Установите соответствие между числом
купленных
банок и количеством банок качественных
консервов:
1)
![]() ,
2)
.
,
2)
.
1 |
|
|
27 |
2 |
|
|
36 |
|
|
|
24 |
№3. Относительная частота выигрыша при покупке лотерейных билетов оказалась равной 0,25. Установите соответствие между числом купленных билетов и количеством невыигравших билетов.
1.
![]() 2.
2.
![]()
1 |
|
|
15 |
2 |
|
|
36 |
|
|
|
5 |
Классическое определение вероятности.
№1. В стопке из 16 конвертов на 7 приклеены марки. Наудачу извлекают 2 конверта. Вероятность того, что на них не будет марок, равна …
|
|
|
|
|
|
|
№2. В урне 5 красных и 7 зеленых шаров. Из урны наудачу берут два шара. Вероятность того, что шары разноцветные, равна …
|
|
|
|
|
|
|
Законы распределения вероятностей дискретных случайных величин.
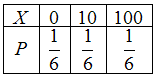
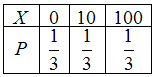
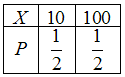
№1. Игрок бросает игральную кость и
получает 10 евро, если выпадает 5 очков,
100 евро, если выпадет 1 очко. В остальных
случаях игрок не получает ничего. Закон
распределения случайной величины
![]() –
сумма, полученная игроком после
броска игральной кости, имеет вид …
–
сумма, полученная игроком после
броска игральной кости, имеет вид …
|
|
|
|
|
|
|
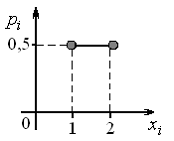
№2. Закон распределения дискретной случайной величины – количество выпадений «гербов» при двукратном подбрасывании монеты, имеет следующее графическое представление …
|
|
|
|
|
|
|
|
|
|
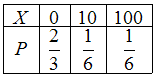
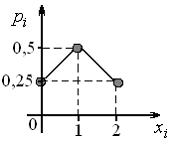
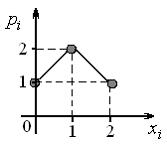
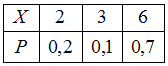
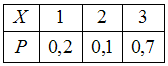
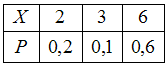
№3. Закон распределения дискретной
случайной величины
,
соответствующий многоугольнику
распределения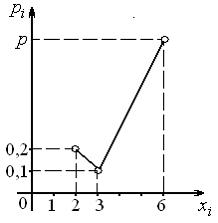 ,имеет
вид:
,имеет
вид:
|
|
|
|
|
|
|
|
|
|