
- •Д ифференциал функции и дифференциал независимой переменной. Таблица производных, интегралов и их взаимосвязь.
- •Основные свойства неопределенного интеграла. Способ непосредственного интегрирования.
- •Метод замены переменной интегрирования.
- •Интегрирование по частям, неопределенный интеграл. Самоприводящиеся интегралы.
- •Приведение рациональных дробей к простейшим.
- •Свойства определенного интеграла. Формула Ньютона-Лейбница.
- •Метод замены переменной интегрирования в определенном интеграле.
Интегрирование по частям, неопределенный интеграл. Самоприводящиеся интегралы.
Совокупность всех первообразных F(x)+c для данной функции f(x) на некотором промежутке Х называется неопределенным интегралом от ф-ции f(x) на этом промежутке; обозн-тся
Этот метод является обращением правила дифференцирования произведения двух ф-ций.
Если ф-ции U(x) и V(x) дифференцируемы, то дифференциал их произведения равен:
d(UV)=UdV+VdU
;
![]() - формула
интегрирования по частям.
- формула
интегрирования по частям.
*произвольную постоянную С указываем в окончательном решении интеграла.
- Заданное подынтегральное выражение f(x)dx представлено в виде UdV.
![]()
- f(x)dx представляем в виде произведения 2х сомножителей U и dV (сначала устанавливаем, какая ф-ция принимается в кач-ве U. Оставшаяся часть выражения будет относиться к дифференциалу dV, причем dx должен входить в состав dV).
- Затем дифференцируем U (надо найти dU), а интегрируем dV (надо определить V). - Имея значение U и dV, можно приступать к вычислению интегралов.
- Рекомендации по выбору: а) U – степенная или алгебраическая ф-ция, dV – показательная или тригонометрическая; б) U –логарифмическая или обратная тригонометрическая, dV – степенная или алгебраическая.
*встречаются случаи, когда интегрирования по частям следует применять последовательно, 2 раза и больше.
* в некоторых случаях интегрирование по частям приводит к выражению, содержащему исходный интеграл. Такие интегралы – самоприводящиеся.
Приведение рациональных дробей к простейшим.
-
Пусть P(x)
и Qx
– многочлены; тогда дробь ![]() называется рациональной дробью.
называется рациональной дробью.
- Рациональная дробь правильная, если степень числителя меньше степень знаменателя. В противоположном случае она – неправильная.
-
Р.Д. может быть представлена в виде
простейших дробей: 1) ![]() ;
2)
;
2) ![]() ;
3)
;
3)![]() ;
4)
;
4)![]() - где А, В, a,
p,
q
– действительные числа, n
– натуральное число.
- где А, В, a,
p,
q
– действительные числа, n
– натуральное число. ![]() имеет комплексные корни, т.е. не
раскладывается на действительные
множители. Простейшие дроби интегрируются
в элементарных функциях. Для определения
коэффициентов в числителях тех простейших
дробей, на которые разлагается данная
РД: 1) способ задания частных значений;
2) способ неопределенных коэффициентов.
имеет комплексные корни, т.е. не
раскладывается на действительные
множители. Простейшие дроби интегрируются
в элементарных функциях. Для определения
коэффициентов в числителях тех простейших
дробей, на которые разлагается данная
РД: 1) способ задания частных значений;
2) способ неопределенных коэффициентов.
Интегрирование рациональных дробей.
Т.к. неправильную РД представляем в виде многочлена и правильной РД, правильную РД всегда можно представить в виде суммы простейших дробей, то интегрирование РД в общем виде сводится к интегрированию многочленов и простейших дробей, которые всегда интегрируются в элементарных функциях.
Пример:
дробь алгебраически приводится к виду:
![]() =
=![]()
 (потому
что производная знаменателя – это
числитель)
(потому
что производная знаменателя – это
числитель)Для инт-ния второй дроби получим в знаменателе полный квадрат (с х).
![]() .
.
Если
 не больше 0, то корни квадратичного
трехчлена действительны.
не больше 0, то корни квадратичного
трехчлена действительны. 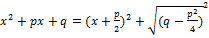 .
.
Получили интеграл вида
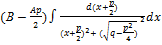 . Табличный интеграл вида
. Табличный интеграл вида 
Интегрирование иррациональных алгебраических выражений (R(xα, xβ, xˠ…)
За исключением частных случаев, иррациональные алгебраические выражения не интегрируются в элементарных ф-циях. Необходимо избавляться от иррациональности.
- α, β, ˠ - дробные рациональные числа; n – наим. Кратное знаменателей дробей α, β, ˠ.
- Интегралы этого вида приводятся к интегралам от рациональной функции подстановкой x=tn: dx=ntn-1dt
-
Интеграл преобразуется к виду ![]() .
При этом nα,
nβ,
nˠ
- целые числа.
.
При этом nα,
nβ,
nˠ
- целые числа.
Пример:
![]() = 6
= 6![]()
Решение:
1/3, 2/3, 1/2- наим. кратным знаменателей является 6.
X=t6;
dx =6t5dt.
![]()
Интегрирование иррациональных алгебраических выражений R(x,
 )
и R(x,
)
и R(x,
 )
)
Один из способов – применение тригоном. подстановок, что позволяет получать подынтегральные выражения рациональные относительно тригон. ф-ций.
1
–
![]() *
*![]()
*X
= sin t (a cos t); ![]() =
=
![]() =a
cos t ; dt = a cos t dt
=a
cos t ; dt = a cos t dt
Аналогично рассматриваем и случаи 2х других интегралов:
2
-
![]() *
a
*
a![]()
*X=a
tg t (x=a ctg t); dx = ![]() ;
(sec x =
;
(sec x =![]() )
)
![]()
3-![]() =*
=*
![]()
*x=a sec t (x=a cosec t); dx=a tg t sec t dt; cosec x=1 / sin x
![]()
Интегрирование тригонометрических функций. Интегрирование тригонометрических функций с помощью подстановки.
1 - Интегрирование выражений sinmx, cosnx; n,m – целые числа – положительные или отрицательные. Пусть хотя бы один из показателей степени нечетный; напр. n.
-cosn
x
= cosn-1
x*cos
X;
n-1
–четное число. ![]() *=
*=
![]()
*произведем замену: sin x =t, cos x dx=dt. Получили интеграл от целой рациональной ф-ции, которая всегда берется в элементарных ф-циях.
-
если показатели степеней m
и n
оба четные, то можно понизить показатели
с помощью формул: ![]() ;
;
![]()
2
-
(t
=![]() ):
от – П до П.Эта подстановка всегда
позволяет выразить sin
x,
cos
x
b
dx
рационально через переменную t.
Иногда её называют универсальной.
):
от – П до П.Эта подстановка всегда
позволяет выразить sin
x,
cos
x
b
dx
рационально через переменную t.
Иногда её называют универсальной.
![]() ;
;
![]() ; dx
= (arctg
t)’dt
=
; dx
= (arctg
t)’dt
= ![]() ;
;
![]() ;
x=2
arctg
t
;
x=2
arctg
t
О
 пределенный
интеграл, геометрический смысл
определенного интеграла. Формула
Ньютона-Лейбница.
- определенный
интеграл:
пусть от a
до b
задана непрерывная ф-ция (неотрицательная).
Мы разделили промежуток на n
произвольных по длине отрезков, назвали
частичными. a<ˠ1<ˠ2…
<b.
Длина i-ого
частичного отрезка через ΔXi
=Xi
– Xi-1.
На каждом частичном отрезке выбираем
точку с абсциссой ˠi.
Сумма произведений
пределенный
интеграл, геометрический смысл
определенного интеграла. Формула
Ньютона-Лейбница.
- определенный
интеграл:
пусть от a
до b
задана непрерывная ф-ция (неотрицательная).
Мы разделили промежуток на n
произвольных по длине отрезков, назвали
частичными. a<ˠ1<ˠ2…
<b.
Длина i-ого
частичного отрезка через ΔXi
=Xi
– Xi-1.
На каждом частичном отрезке выбираем
точку с абсциссой ˠi.
Сумма произведений .
.
-
Составили предел этой суммы (полагаем,
что длина каждого отрезка уменьшается
и → 0 и кол-во их увелич-ся и →∞.
![]() - этот предел называет определенным
интегралом ф-ции f(x)
на
промежутке [a;b]
и обозначается
- этот предел называет определенным
интегралом ф-ции f(x)
на
промежутке [a;b]
и обозначается ![]()
![]()
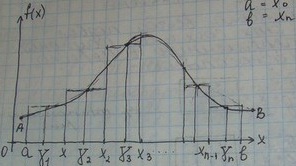
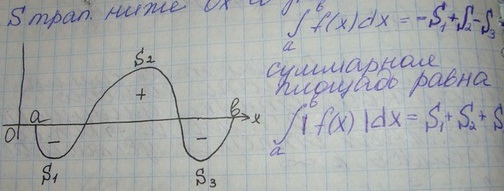
- геометрический смысл определенного интеграла: фигура, ограниченная непрерывной кривой y=f(x) и кривыми линиями x=a, x-b, y=0 – криволинейная трапеция. Определенный интеграл непрерывной неотриц-й ф-ции при a<b = площади соответствующей криволин. трапеции. В общем случае интеграл представляет собой алгебраическую сумму площадей соответствующих криволинейных трапеций, где площади трапеций располагающихся выше оси ОХ берутся со знаком +, а ниже – со знаком -.
- Формула
Ньютона-Лейбница:
Формула
Ньютона-Лейбница:![]()
Более подробно о формуле – см. 11 билет.
