• Нельзя один общий заголовок или его вместе с заголовками граф оставлять на предыдущей странице, а цифровые данные переносить на следующую страницу;

• Нельзя переносить на следующую страницу одну итоговую строку;

• При переносе нужно либо повторить полные заголовки граф, либо дать их нумерацию и сверху написать «Продолжение (окончание) таблицы…»

• 16. Охарактеризовать абсолютные статистические величины

• Абсолютные статистические показатели - это показатели, выражающие размеры общественных явлений и процессов.

• Размеры общественных явлений могут быть выражены либо в виде суммарной численности единиц совокупности (например, число п/п, число банков, число работающих, численность населения),либо в виде суммарной величины признака, характеризующего изучаемую совокупность (например, объём продукции обследуемы п/п, фонда заработной платы работающих, денежные доходы населения).

• По способу выражения размеров количественных явлений и процессов абсолютные статистические величины подразделяются на индивидуальные и суммарные (итоговые).

• Индивидуальные – это показатели, характеризующие размеры количественных признаков у отдельных единиц изучаемой совокупности (например, номинальная зарплата одного работающего фирмы; размер посевной площади, занятой под одной культурой занятой в с/х п/п; розничный товарооборот одного магазина). Индивидуальные абсолютные величины получают в результате проведения статистического наблюдения.

• Суммарные (итоговые) – показатели, характеризующие размеры количественных признаков у всех единиц изучаемой совокупности или у отдельных их групп (например, номинальная зарплата всех работающих фирмы; размер посевной площади, занятой под всеми культурами в с/х п/п; розничный товарооборот всех обследованных магазинов). Суммарные (итоговые или групповые) абсолютные величины являются результатом сводки данных статистического наблюдения. Их получают либо суммированием индивидуальных абсолютных величин, либо путём подсчёта числа единиц, составляющих отдельные группы или всю совокупность.

• Абсолютные статистические величины, как правило, являются именованными величинами. В зависимости от задач исследования и характера изучаемых явлений они могут быть выражены в натуральных, условно-натуральных, стоимостных(денежных), трудовых и комбинированных(сложных) единицах измерения.

• 17. Охарактеризовать относительные статистические величины

• Относительные статистические показатели – обобщающие статистические показатели, выражающие количественные соотношения размеров социально-экономических процессов и явлений. Они получаются путём деления одной статистической величины на другую. При этом та величина, с которой сравнивают(знаменатель), называется основанием, базой сравнения или базисной величиной, а сравниваемая величина(числитель) – текущей или отчётной величиной.

• Относительными величинами динамики называются статистические величины, характеризующие степень развития изучаемого явления во времени. Эти величины также называют темпами роста.

• Относительные величины планового(нормативного) задания рассчитываются как отношение уровня показателя, запланированного(нормативного) на предстоящий(планируемый) период, к его уровню, достигнутому за предшествующий или базисный период.

• Относительные величины выполнения планового(нормативного) задания представляют собой отношение фактически достигнутого в отчётном периоде уровня показателя к запланированному(нормативному) заданию.

• Относительные величины динамики, планового(нормативного) задания и выполнения планового(нормативного) задания связаны между собой след. соотношением: относительная величина динамики равна произведению относительных величин планового(нормативного) задания и выполнения планового(нормативного) задания.

• Относительные величины структуры представляют собой соотношение размеров отдельных частей изучаемой совокупности и совокупности в целом. Они характеризуют состав совокупности и показывают какую долю(или удельный вес) во всей совокупности составляют её отдельные части. Выражаются в процентах или коэффициентах.

• Относительные величины координации представляют соотношение отдельных частей целого между собой. При расчёте относительных величин координации одну из составных частей целого принимают за базу, а затем находят отношение к ней всех остальных частей.

• Относительные величины интенсивности представляют собой показатели, характеризующие степень распространения или развития того или иного явления в определённой среде. Они рассчитываются путём сопоставления абсолютных величин, относящихся к различным совокупностям, но находящимся между собой в определённой связи.

• Относительные величины сравнения представляют собой соотношения одноименных статистических величин, относящихся к разным объектам или разным территориям. Рассчитываются они, как правило, за один и тот же период времени или на определённый момент времени.

• Относительные величины уровня экономического(социального) развития представляют собой статистические показатели, характеризующие размеры производства или потребления различных видов продукции, доходов и других показателей на душу населения.

• 18. Изложить сущность средних величин

• Под средней величиной понимают обобщающую количественную характеристику единиц совокупности по определённому варьирующему признаку.

• Сущность метода средних величин заключается в том, что множество фактических значений определённого признака единицы совокупности заменяется одной величиной, отражающей типичный, характерный уровень признака. Таким образом, средняя величина, абстрагируясь от индивидуальных особенностей отдельных единиц, отражает то общее, что присуще всем единицам исследуемой совокупности.

• 19. Назвать и охарактеризовать виды средних величин.

• Средняя величина – обобщающая количественная характеристика единиц совокупности по определённому варьирующемуся признаку.

• Виды средних величин:

• 1.Срядняя арифметическая

• *простая – расчёт среднее осуществляется по несгруппированным данным, представленных в виде индивидуальных значений признака у отдельных единиц совокупности.

• *взвешенная- если индивидуальные значения признака единиц совокупности повторяются несколько раз, то средняя определяется по сгруппированным данным, которые могут быть представлены в виде рядов распределения (дискретных или интервальных)

• 2.Средняя гармоническая

• *простая- представляет собой среднюю из обратных значений признака единиц совокупности.

• *взвешенная – используют, когда известны варианты признака (х) И произведения вариант на их частоту (xf), а непосредственно частота признака неизвестна.

• 3.Средняя геометрическая

• 4.Средняя квадратическая

• 20. Охарактеризовать структурные средние величины

• Различают структурные средние величины к ним относят:

• Мода – величина признака которая встречается в ряде распределения с наибольшей частотой.

• M_o=x_mo +i_mo(f_mo-f_mo-₁/(f_mo- f_mo-₁)+(f_mo+f_mo+1))

• X_mo- нижняя граница модального интеграла

• F_mo-частота модального интеграла

• F_mo-1 –частота интервала предшествующего модальному

• i_{mo –} величина модального интервала

• f_mo+1 – частота интервала следующего интервала

• Медиана- величина признака единицы совокупности находящейся в середине упорядоченного ряда.

• M_e=x_me+i_me(E_f –S_me-1/f_me)

• X_me – нижняя граница медианового интервала

• i_me- величина медианового интервала

• S_me-1-накопленный итог численности до медианного интервала

• F_me-численность медианного интервала

• 21. Назвать и охарактеризовать виды показателей вариации

• Вариация - изменение величины признака от одной совокупности к другой.

• Виды вариации:

• 1.К абсолютным показателям вариации относятся:

• *Размах вариации - разница между максимальным и минимальным значением признака;

• *Среднелинейное отклонение – представляет собой среднюю величину из абсолютных отклонений значений признака каждой единицы совокупности от средней арифметической;

• *Дисперсия – средняя из квадратов отклонений отдельных значений признака от их среднее величины;

• *Среднеквадратическое отклонение;

• 2.К относительным показателям вариации относятся:

• *линейный коэффициент вариации;

• *простой коэффициент вариации;

• *коэффициент осцилляции;

• Вопрос № 22

• Изложить сущность динамических рядов.

• Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение размеров общественных явлений во времени. Ряд динамики состоит из двух основных элементов : во-первых, моментов или периодов времени (t), к которым относятся анализируемые данные; во-вторых, соответствующих им статистических показателей, которые называются уровнями динамического ряда (y).

• В зависимости от характера отображаемого явления, а также от вида статистических данных ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом исходными являются ряды абсолютных величин. Ряды динамики относительных и средних величин являются производными. В свою очередь ряды динамики могут быть представлены либо моментальными, либо интервальными рядами. В зависимости от полноты, с которой отражается период времени, как в моментных, так и в интервальных рядах, их делят на полные и неполные.

• Вопрос № 23

• Дать понятие и классификацию динамических рядов

• Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение размеров общественных явлений во времени. В зависимости от характера отображаемого явления, а также от вида статистических данных ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом исходными являются ряды абсолютных величин. Ряды динамики относительных и средних величин являются производными. . В свою очередь ряды динамики могут быть представлены либо моментальными, либо интервальными рядами. Если уровни ряда динамики выражают состояние явления на определённые моменты времени, то такие ряды называются моментальными. Если уровни ряда динамики характеризуют размеры общественных явлений за определённые интервалы (периоды), то такие ряды называются интервальными. В зависимости от полноты, с которой отражается период времени, как в моментных, так и в интервальных рядах, их делят на полные и неполные. В полных рядах периоды следуют друг за другом с равными интервалами.В неполных рядах в отображаемых уровнях хронологическая последовательность не соблюдается. Полные ряды называют рядами динамики с равностоящими, а неполные-с неравностоящими уровнями..Ряды динамики относительных величин, представляют ряды показателей, характеризующих темпы роста (снижения) изучаемого явления, изменение его структуры. К рядам динамики средних величин относятся ряды показателей, отражающих среднее значение изучаемого явления за определённые периоды времени (ср.зарплата, ср.размер пенсии и т.д)

• Вопрос № 24

• Охарактеризовать аналитические показатели динамики

• При изучении динамики общественных явлений рассчитывают систему аналитических показателей:абсолютные приросты, темпы роста, темпы прироста и абсолютное содержание 1 % прироста либо снижения. Если каждый уровень ряда сравнивают с его предыдущим уровнем, то получаются цепные показатели. Если же каждый уровень уровень сравнивается с начальным показателем, или каким-либо другим, принятым за постоянную базу сравнения, то получают базисные показатели динамики. При этом сравниваемый уровень называется текущим, а тот уровень,который сравнивают,-базисным. Абсолютный прирост-это разность двух уровней ряда динамики, может иметь положительный или отрицательный знак,в последнем случае это будет не прирост, а снижение.. Темп роста-отношение двух уровней ряда динамики. Если темп роста меньше 1,то имеет место не рост, а снижение анализируемого уровня. Темп прироста-отношение абсолютного прироста к уровню, принятому за базу сравнения. Может иметь + или -.

• 25 Вопрос

• Охарактеризовать средние показатели динамики

• Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. Он называется также средней хронологической или временной средней и рассчитывается для разных рядов динамики по –разному.

• В интервальных рядах с равными отрезками применяется средняя арифметическая простая:

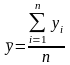• , где n-число уровней ряда

• В интервальных рядах с неравным отрезками используется ср-яя ариф.-ая взвешенная:

• 

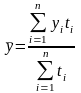
• , где 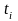-продолжительность i-го отрезка времени

• В моментных рядах с равными промежутками между датами средний уровень рассчитывается по формуле: , где n-число дат, (n-1)-число равных промежутков времени.

• Средний абсолютный прирост показывает, на сколько единиц в среднем увеличился или уменьшился уровень динамического ряда за соответствующий период времени (за месяц, квартал и т.д). Он рассчитывается по средней арифметической простой формуле из цепных абсолютных приростов за последовательные и равные по продолжительности периоды:

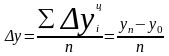• , где n- число цепных абсолютных приростов.

• Средний темп роста рассчитывается по средней геометрической формуле из цепных темпов роста, выраженных в коэффициентах с равными отрезками времени

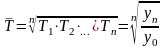• , где n-число цепных темпов роста

• Средний темп прироста показывает, на сколько % в среднем за единицу времени увеличился или уменьшился уровень ряда динамики. Он рассчитывается как разность между сред. темпом роста ( 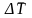) и 100%

• Если выражен в %

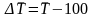
• Вопрос 26

• Изложить сущность, значение и классификацию индексов.

• Индексом в статистике называется относительный показатель, характеризующий изменение во времени, по сравнению с планом или в пространстве уровней социально-экономических явления. Индекс – это особая относительная величина, которая позволяет соизмерять как однородные явления, так и непосредственно несоизмеримые явления .Он всегда получается путём соотношения двух величин: отчётной (или текущей), т. е сравниваемой, и базисной, т.е той, с уровнем которой происходит сравнение отчётной величины.

• Если за базу сравнений берётся уровень явления за какой-то прошлый период времени, то получают динамические индексы.

• Если за базу сравнения берётся уровень явления на другой территории , то получают территориальные индексы.

• Если же за базу сравнения берётся какой-либо нормативный уровень, то получают индексы выполнения плана ,индексы выполнения норм.

• Индексы, рассчитанные для отдельных единиц или элементов, называются индивидуальными, а индексы, рассчитанные для сложных социально – экономических явления,- общими.

• Выражается индекс в виде коэффициента, если за основание принимается единица, или в виде процентов, если за основание принимается сто.

• Вопрос 27

• Охарактеризовать индивидуальные индексы

• К индивидуальным относятся индексы, характеризующие изменение выпуска одного какого-либо вида продукции (индексы производства стиральных машин, индексы производства молока и др.), индексы, характеризующие изменение цены какого-либо товара (электропылесосов, растительного масла и др.), индексы характеризующие изменение себестоимости отдельных изделий и т.д.

• Индивидуальные индексы обозначаются латинской буквой «i».

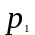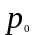• Исходя из определения, индивидуальный показатель динамики – это отношение уровня однородного явления в отчётном периоде к его уровню в базисном периоде. Например, отношение цены какого-либо товара в отчётном периоде ( ) к его цене в базисном периоде ( ) даёт индивидуальный индекс цен ( )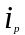

• 

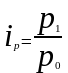
• 28. Охарактеризовать общие индексы (агрегатные)

• Общие индексы служат для сопоставления непосредственно несоизмеримых, разнородных явлений. Например, с помощью общих индексов можно охарактеризовать динамику всей продукции отрасли или динамику объёма всей продукции, выпускаемой в республике

• Чтобы сделать сопоставимыми несоизмеримые явления (пли их составные элементы), нужно выразить их общей мерой: стоимостью, трудовыми затратами и т. д. Эта задача решается путём построения и расчёта общих индексов. Основной формой общих индексов являются агрегатные индексы.

• Агрегатный индекс состоит из: а) индексируемого показателя, изменение которого он должен отражать; б) показателя- со измерителя, который называется весом и должен быть экономически тесно связан с индексируемой величиной

• Значение индексируемой величины всегда изменяется: отчётное значение сопоставляется с базисным. Конкретное название индекса всегда даётся по индексируемой величине.

• Показатель-со измеритель выполняет функцию веса по отношению к индексируемой величине. Значение соизмерителя (веса) в конкретном индексе принимается неизменным, так как он не должен искажать оценку изменения индексируемого показателя. Веса индексов могут быть выражены в стоимостных, трудовых и других единицах измерения, а также в виде относительных величин структуры.

• В зависимости от содержания и характера индексируемой величины различают индексы количественных (объёмных) показателей и индексы качественных показателей.

• Количественные показатели имеют чисто количественный, объёмный характер и характеризуют общий, суммарный размер того или иного явления.

• Качественные показатели носят качественный характер и характеризуют уровень явления в расчёте на единицу совокупности. Как правило, качественные показатели представляют собой либо средние, либо относительные величины.

• При этом существует правило построения агрегатных индексов, в соответствии с которым в индексах качественных показателей веса берутся обычно на уровне отчётного периода, а в индексах количественных (объёмных) показателей — на уровне базисного периода.

• Таким образом, общий агрегатный индекс цен определяется по формуле

• 

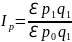
• Общий агрегатный индекс физического объёма продукции (товарооборота)

• 

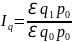
• Индексный метод даёт возможность определить изменение явления не только в относительном, но и в абсолютном выражении. Для этого необходимо из числителя соответствующего общего индекса вычесть его знаменатель.

• ♦ уровней цен

• ♦ физического объёма продукции

29. Средние Индексы

Общий индекс может быть исчислен и как средняя величина из индивидуальных индексов. Эта средняя может быть рассчитана как ср. арифмет. И как ср. гармоническая. Выбор формы индекса зависит от исходных данных и изучаемого признака. Ср. Индексы применяются, когда отсутствуют данные о величине индексируемого показателя и соизмерителя, а известны изменения величины индексируемого показателя.

Средняя величина – обобщённая количественная хар-ка единиц совокупности по определённому варьирующему признаку.

Все средние величины могут быть простыми и взвешенными.

Если расчёт ср. осущ-ся по несгруппированным признакам – то считаем по простой, если индивидуальные признаки повторяются несколько раз – то по взвешенной.

Кроме арифметической применяют также гармоническую величину(применяется когда известна частота колебания). Она является обратной средней арифметической.

30.Охарактеризовать индексы средних показателей.

Для изучения изменения таких показателей(средняя величина единицы продукции ,средняя себестоимость единицы изделия, средняя з/п одного работника, средняя трудоёмкость одного изделия.) в статистической практике применяются индексы средних величин в виде индексов переменного и постоянного (фиксированного) состава и индексов структурных сдвигов.

Индекс переменного состава равен соотношению средневзвешенных уровней изучаемого показателя. Этот индекс характеризует изменение средней цены единицы продукции в целом за счет двух факторов 1.изменения цены единицы продукции на каждом заводе ;2.изменения удельного веса производства продукции на каждом из анализируемых заводов, т е за счет влияния структурных сдвигов. Влияние каждого из этих факторов на динамику средней цены продукции можно выявить при помощи расчета, соответственно, индекса цены постоянного ( фиксированного) состава и структурных сдвигов .

Индекс структурных сдвигов . этот индекс характеризует изменение средней цены единицы продукции только за счет изменения удельных весов количества произведенной продукции на отдельных заводах.

№ 31

Графики применяются, чтобы сделать результаты статистического наблюдения, сводки и группировки статистических данных наглядными, более понятными и запоминающимися.

Главным достоинством графического метода является то, что он служит средством лаконичного, компактного и наглядного представления статистических данных. Статистический график в отличие от таблицы даёт обобщающую картину состояния или развития того или иного явления, позволяет держаться в цифровом статистическом материале.

Исключительно большое значение графического способа проявляется в том, что он служит мощным орудием обобщения и анализа статистических данных, а в некоторых случаях – единственным и незаменимым способом их исследования.

Графики дают целостную картину явлений и процессов, обобщающее представление о них и помогают осмыслить статистический материал. При графическом изображении статистических данных становятся особенно отчётливыми и наглядными взаимная связь между явлениями и процессами общественной жизни, основные тенденции их развития, степень распространённости их в пространстве и др.

В настоящее время графики вошли не только в науку, но в практику экономической и статистической работы. Многие процессы графического изображения цифровых данных реализованы в различных статистических пакетах, в системах статистического анализа и Пэвм.

№ 32

Графиками в статистике называются условные изображения статистических величин и их соотношений в виде различных геометрических образов: точек, линий, плоских фигур и т.п. Если рассматривать статистический график как плоскостное изображение, то в нём можно выделить графический образ и вспомогательные элементы.

Графический образ(основа графика) – геометрические знаки, совокупность точек, линий и фигур, с помощью которых изображаются статистические величины. Применяемые геометрические знаки определяют вид графика. Графический образ должен соответствовать цели графика и быть максимально выразительным, чтобы правильно изобразить статистические данные.

Вспомогательными элементами графика являются: поле графика, пространственные ориентиры, масштабные ориентиры, экспликация графика.

Поле графика – пространство размещения знаков, имеющее определённые размеры и пропорции(соотношения) сторон. Размер поля зависит от назначения графика: в литературных источниках используются небольшие графики, а на стендах, витринах, выставках – довольно крупные. Что касается пропорций, то в этом отношении наиболее часто встречаются графики с неравными сторонами, но иногда они подаются и в виде квадратов.

На практике обычно применяется следующее соотношение неравных сторон графиков: от 1:1,33 до 1:1,5.

Пространственные ориентиры определяют размещение геометрических знаков на поле. Они зависят от принятой системы координат. В статистических графиках наиболее часто применяется система прямоугольных координат.

Масштабные ориентиры дают геометрическим знакам количественную определённость. Сюда относятся эталоны знака, масштаб графика и масштабная шкала.

Эталоны знака отражают величину геометрических знаков, изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика.

Масштаб графика – условная мера перевода числовой величины в графическую. Масштабная шкала – это линия, отдельные точки которой могут быть прочитаны как определённое значение статистического показателя. В статистических графиках обычно применяются: а) прямолинейные масштабные шкалы, которые, как правило, располагаются по осям координат; б) криволинейные масштабные шкалы, например круговые, которые применяются в секторных диаграммах.

Масштабные шкалы бывают:

• Равномерные, в которых отрезки пропорциональны числам;

• Неравномерные, например, логарифмические масштабные шкалы, в которых отрезки пропорциональны не числам, а их логарифмам.

Шкала, по которой отсчитываются уровни явлений, как правило, начинается с нуля.

Если строится линейный график, занимающий лишь верхнюю часть поля, то нижняя часть может быть исключена путём разрыва шкалы.

Границы шкалы обычно показываются двумя волнистыми линиями.

Исключение части шкалы даёт возможность при том же размере графика укрупнять масштаб.

Экспликация графика – словесное объяснение содержания графика и значения каждого его геометрического знака. Она включает в себя:

А) название графика – общий заголовок, кратко точно раскрывающий основное содержание графика;

Б) подписи вдоль масштабных шкал;

В) пояснения к отдельным частям графика;

Г) числовые данные, которые дополняют или уточнят величину нанесённых на график показателей.

№ 33

По характеру применяемых графических образов графики разделяются на:

• Точечные, в которых в качестве графических образов применяются совокупности точек;

• Линейные, где графическим образом выступают отрезки прямых и кривых линий;

• Столбиковые;

• Полосовые;

• Квадратные;

• Круговые;

• Фигурные.

По характеру изображаемых статистических показателей или с точки зрения реаемых задач выделяют графики:

• Сравнения статистических показателей;

• Структуры экономических явлений;

• Динамики;

• Контроля выполнения плана;

• Взаимосвязанных статистических показателей;

• Графики вариационных рядов;

• Графики пространственного размещения и пространственной распространённости;

• Комбинированные, которые одновременно решают несколько задач, например, изображают структуру и её изменение во времени.

По способу построения графики делятся на:

• Диаграммы – графическое изображение в системе координат статистических величин при помощи геометрических фигур или знаков; территория, к которой относятся эти величины, указана только словесно;

• Картодиаграммы – диаграммы, наложенные на карту или план территории, которой относятся изображаемые величины;

• Картограммы – изображение величины показателя путём штриховки или раскраски соответствующей территории на карте или плане.

Картограммы и картодиаграммы служат для совместного изображения экономической и географическ4ой характеристик исследуемых явлений. Например, они могут показывать не только расположение изучаемого явления, но и его интенсивность на конкретной административной или экономической территории.