13. Исследование знакопеременных рядов на абсолютную сходимость.

Проще всего исследовать знакопеременный числовой ряд на абсолютную сходимость. В этом случае берем знакоположительный ряд 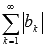, составленный из абсолютных величин членов исходного ряда, и применяем к нему подходящий достаточный признак сходимости из рассмотренных выше. Если ряд сходится, то исходный ряд является абсолютно сходящимся. Пример. Докажите, что знакопеременный числовой ряд 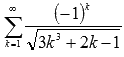абсолютно сходится. Решение. Соответствующих знакоположительный ряд будет иметь вид 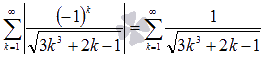. Для него выполняется необходимое условие сходимости ряда, так как . Возьмем сходящийся знакоположительный ряд 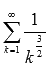и воспользуемся вторым признаком сравнения: 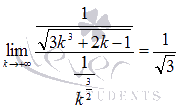. 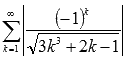Следовательно, ряд сходящийся, поэтому, исходный ряд сходится абсолютно.

14 функциональный ряд Функциональным рядом называют выражение  u₁(x)+u₂(x)+...+u_n(x)+... ,  где каждый член ряда в сущности является функцией. Обычно сходимость такого ряда зависит от значения x.

область сходимости функционального ряда называют совокупность значений x, при котором ряд сходится.

Функциональный ряд, его сходимость. Рассмотрим ряд,  , членами которого являются функции, определенные на промежутке  . При каждом фиксированном  имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда  также является функцией от х:  . По определению предела последовательности: если для  можно указать номер  ( что интересно, для каждого фиксированного   - свой номер, т.е. ), такой, что для    выполняется неравенство  , то это и означает, что функциональный ряд сходится к функции . Множество , для которого это выполняется, называется областью сходимости функционального ряда.

 

ПРИМЕР 1.  Нахождение области сходимости функционального ряда.

Равномерная сходимость функционального ряда. Пусть  , т.е. функциональный ряд сходится. Если для   можно указать номер  независимо от  , такой, что для выполняется неравенство  , то говорят, что функциональный ряд сходится равномерно на множестве .  

 

ПРИМЕР 2.  Изучение сходимости функционального ряда.

 

Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд  с положительными членами, такой, что для всех  , начиная с некоторого номера и всех  выполняется неравенство , то функциональный ряд  сходится на равномерно. Числовой ряд  в этом случае называют мажорантой для функционального ряда.

15. Степенные ряды – важный частный случай функциональных рядов (см. Ряд) – ряды вида

,

где коэффициенты ряда а₀, а₁, … – некоторые постоянные.

Ряды можно рассматривать как в вещественной (действительной), так и в комплексной области.

В действительной области множество сходимости степенного ряда – внутренность интервала |x| < r, т.е. множество чисел х, таких, что –r < x < r. Граничные точки интервала сходимости могут как принадлежать, так и не принадлежать (один или оба) множеству сходимости степенного ряда.

В комплексной области множество сходимости ряда – внутренность круга радиуса r. Граничные точки этого круга могут как принадлежать, так и не принадлежать области сходимости ряда.

Область сходимости ряда может вырождаться в точку (r = 0), во всю прямую в случае действительного переменного или во всю комплексную плоскость (r = ∞).

Пример 1

Область сходимости ряда

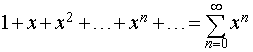
– бесконечной геометрической прогрессии с первым членом, равным 1, и знаменателем, равным х, как объясняется в школьном курсе, – интервал –1 < x < 1; на концах этого интервала ряд расходится. На указанном интервале данный ряд сходится к функции

Для степенных рядов справедливы следующие утверждения:

Теорема 1.

Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S⁽ⁿ⁾(x).

Теорема 2.

Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если х  (-R; R), причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны 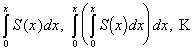 .