1) Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме

А лгебраическая форма

Запись комплексного числа z в виде x + iy, , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i² = − 1):

(a + ib) + (c + id) = (a + c) + i(b + d);

Действия над комплексными числами

Сравнение

a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Сложение

(a + bi) + (c + di) = (a + c) + (b + d)i.

Вычитание

(a + bi) − (c + di) = (a − c) + (b − d)i.

Умножение

(a+bi)*(c+di)=

=ac+bci+adi-bd=(ac-bd)+(bc+ad)i 

Деление

2) Комплексное число как пара вещественных чисел. Основные свойства пар. Обоснование свойств комплексных чисел.

К омплексное число z можно определить как упорядоченную пару вещественных чисел (x,y). Введём операции сложения и умножения таких пар следующим образом:

В ещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида  (x,0) , причём операции с такими парами согласованы с обычными сложением и умножением ввенных чисел. Ноль представляется парой 

е диница –

а  мнимая единица –

  На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен  , то есть − 1.

Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные сотношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно

6) Схема Горнера. Разложение по степеням х-с. Краткая схема Горнера.

Задан многочлен P(x):

.

Пусть требуется вычислить значение данного многочлена при фиксированном значении x = x₀. Представим многочлен P(x) в следующем виде:

.

Определим следующую последовательность:

…

…

Искомое значение P(x₀) = b₀. Покажем, что это так.

В полученную форму записи P(x) подставим x = x₀ и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через b_i:

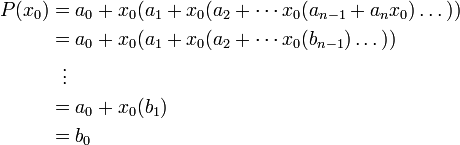
Использование схемы Горнера для деления многочлена на бином

При делении многочлена   на  получается многочлен   с остатком  .

При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:

,  .

Таким же образом можно определить кратность корня (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням :