50. Распространение плоской электромагнитной волны в однородном проводящем полупространстве

П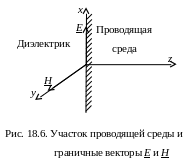 усть однородная проводящая среда простирается теоретически в бесконечность. Участок проводящей среды представлен на рис. 18.5.

Так как падающая волна в толще проводящей среды не встречает границы, то отраженной волны в этом случае не возникает.

Постоянную C₁ найдем из граничных условий. Если обозначить напряженность магнитного поля на поверхности проводящей среды через , то при z = 0 C₁ = H₀.

(18.19)

Чтобы записать выражения для мгновенных значений Н и Е, необходимо правые части (18.19) умножить на и взять мнимые части от полученных произведений:

(18.20)

П о мере проникновения электромагнитной волны в проводящую среду амплитуды Е и Н уменьшаются по показательному закону (рис.18. 6).

Мгновенные значения Н и Е определяются аргументом синуса, который в (18.20) зависит от z и t. Если принять t = const, то на рис. 18.6 Н(z) будет представлена кривой 1 при t + ₀ = 0 и кривой 2 – при t + ₀ = 90^o.

Для того, чтобы охарактеризовать быстроту уменьшения амплитуды падающей волны по мере ее проникновения в проводящую среду, вводят понятие «глубина проникновения».

Глубина проникновения и длина волны

Под глубиной проникновения понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшается в е = 2,71 раз.

(18.21)

Глубина проникновения зависит от свойств среды ( и ) и частоты . Пусть f = 5000 Гц,  = 10⁷ (Омм)^-1 и = 10³, то k = 14100 м^-1,  = 7710^-5 м (0,007 см).

Под длиной волны в проводящей среде понимают расстояние вдоль направления распространения волны, на котором фаза колебания изменяется на 2 радиан

(18.22)

Для рассмотренного выше примера: l = 0.000445 м.

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело бы одну и ту же фазу. Фаза колебаний – t – kz + _a.

(18.23)

В рассмотренном примере v_ф = 2.25 м/с.

Глубина проникновения и фазовая скорость зависят от характеристик материала  и .

Комплексное число p = k + jk – это коэффициент распространения волны, действительная часть его соответствует коэффициенту затухания, а мнимая – коэффициенту фазы. Но они отличаются от подобных коэффициентов в уравнениях для длинной линии, так как в этом случае волна движется вглубь проводника, а не вдоль.

Вектор Пойнтинга в какой-либо точке проводника

где

После некоторых преобразований можно записать

Тогда

(18.24)

Активная составляющая вектора Пойнтинга

(18.25)

При z = 0 , а при z =  .

Следовательно, разница потоков энергии в пределах глубины проникновения составляет

(18.25)

Это означает, что в пределах слоя, толщина которого равна глубине проникновения, выделяется более 85% электромагнитной энергии.

51. Электрический поверхностный эффект

Рассмотрим проводник в виде шины (рис. 18.7). Предположим, что 2a << h, h << l. По проводнику протекает ток I. В любом поперечном сечении характер распределения напряженности магнитного поля одинаков.

Требуется выяснить распределение напряженности электрического и магнитного полей по сечению шины.

Т ак как у шины имеется две границы, то могут возникать прямые и обратные волны. Поэтому решение дифференциальных уравнений второго порядка имеет вид:

. (18.26)

Разместим начало системы координат посредине шины и сориентируем ее таким образом, чтобы векторы напряженностей электрического и магнитного полей имели составляющие только по одной координате.

Постоянные интегрирования определим из граничных условий:

– при x = – a H = H₀,

– при x = a H = –H₀.

Тогда из системы уравнений (18.26) следует:

Последовательной подстановкой получаем:

Следовательно,

(18.27)

Подставив эти значения в уравнения (18.26), получим

Учитывая, что на границе шины

получим

Окончательно мы имеем

(18.28)

Рассмотрим, как изменяются соотношения E/E₀ и H/H₀ по сечению шины. Так как коэффициенты затухания и фазы для проводящей среды равны, то

Тогда

(18.29)

Так как величина a является числом, то характер зависимостей E/E₀ и H/H₀ определяется характеристиками материала шины и частотой. Эти зависимости представлены на рис. 18.8.

Т ак как , то напряженность электрического поля не уменьшается до нуля. В то же время , поэтому напряженность магнитного поля в середине шины (при х = 0) равна нулю.

При  = 0 (постоянный ток) величина напряженности электрического поля определяется вектором плотности тока и не зависит от положения рассматриваемой области. Аналогичная картина наблюдается при частотах, близких к нулю. В этом случае говорят о квазистатическом распределении поля.

При повышении частоты картина распределения плотности тока, а, следовательно, и напряженности электрического поля меняется. Большее значение напряженности наблюдается по краям пластины и спадает во внутренней части. Возникает поверхностный эффект.

В другом крайнем случае (при ) ток будет протекать только по поверхности шины.