Функция распределения случайной величины и ее свойства

Ряд распределения (и, соответственно, многоугольник распределения) могут быть построены только для дискретной случайной величины (для недискретной они не могут быть построены хотя бы потому, что множество возможных значений такой случайной величины несчетно, и их нельзя перечислить в верхней строке таблицы). Наиболее общей формой закона распределения, пригодной для всех случайных величин (как дискретных, так и недискретных), является функция распределения.

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем заданное х:

(5.7)

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки х (на рисунке 5.5) соответствующая часть оси абсцисс, т. е. множество точек, представляющее событие (X < х), отмечена штриховкой).

Функцию распределения иногда называют также интегральной функцией распределения. Функцию распределения — самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Основные свойства функции распределения

1. Функция — всегда неотрицательна, т.е. для всех x.

2. — неубывающая функция своего аргумента, т. е. при .

3. Значения функции заключены между 0 и 1: .

4. .

Зная функцию распределения F(x) случайной величины X, можно вычислять вероятности любых событий, с нею связанных.

Выражение вероятности попадания на участок через функцию распределения

(5.8)

т. е. вероятность того, что значение случайной величины X заключено в интервале от до и равно разности значений функции распределения, вычисленных в точках x и .

Формула (5.5) справедлива для любых случайных величин — как дискретных, так и недискретных.

Плотность распределения

Рассмотрим дискретную случайную величину X, имеющую очень много возможных значений, расположенных очень близко друг к другу на числовой оси, и построим ее функцию распределения (рисунок 5.6). По мере увеличения числа возможных значений и уменьшения интервалов между ними число скачков становится все больше, а сами скачки - все меньше.

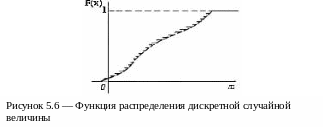
Ступенчатая линия приближается к плавной, непрерывной (см. пунктирную линию на рисунке 5.6). Естественной идеализацией такого положения является случай, когда функция F(x) непрерывна.

Условимся называть случайную величину X непрерывной, если ее функция распределения не только непрерывна в любой точке, но и дифференцируема всюду, кроме, может быть, отдельных точек, где она терпит излом (рисунке 5.7).

В качестве закона распределения, имеющего смысл только для непрерывных случайных величии, введем понятие плотности распределения или плотности вероятности.

Вероятность попадания с. в. на участок равна приращению функции распределения на этом участке; поэтому средняя плотность на участке от до будет равна

. (5.9)

Переходя к пределу при , получим плотность в точке :

, (5.10)

а это — не что иное, как производная функции распределения.

Таким образом, плотностью распределения (или плотностью вероятности, иногда просто плотностью) непрерывной случайной величины в точке называется производная ее функции распределения в этой точке. Обозначим ее :

. (5.11)

Так же, как и аргумент функции распределения, аргумент плотности может быть обозначен любой буквой; f(x) и f(t) — одна и та же функция, только с по-разному обозначенным аргументом.

Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения; в отличие от функции распределения, эта форма не универсальна: она существует только для непрерывных случайных величин.

График плотности распределения f(x) называется кривой распределения (рисунок 5.8).

Введем важное понятие: элемент вероятности. Рассмотрим непрерывную с. в. X с плотностью f(x) и элементарный участок dx, примыкающий к точке х (рисунок 5.8).

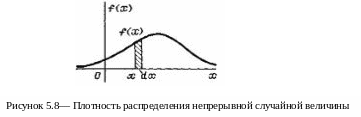
Вероятность попадания с. в. X на этот участок dx (с точностью до бесконечно малых высших порядков) равна f(x)dx. Величина f(x)dx называется элементом вероятности для точки х. Геометрически элемент вероятности приближенно равен площади элементарного прямоугольника, опирающегося на отрезок dx, примыкающий к точке х (заштрихована на рисунке 5.8). Выразим вероятность попадания с. в. X на участок от x₁ до x₂ (рисунок 5.9). Очевидно, вероятность попадания с.в. X на участок (x_1,x₂) равна сумме элементов вероятности на всем этом участке, т. е. интегралу:

. (5.12)

В геометрической интерпретации эта вероятность равна площади, ограниченной сверху кривой распределения и опирающейся на участок (x_1,x₂) (заштрихована на рисунке 5.9).

Формула (5.12) сразу же дает возможность выразить функцию распределения F(x) через плотность распределения f(x). Действительно,

. (5.13)

В геометрической интерпретации функция распределения равна площади, ограниченной сверху кривой распределения и лежащей левее точки х (на рисунке 5.10 эта площадь заштрихована).

Укажем основные свойства плотности распределения f(x):

1. Плотность распределения — неотрицательная функция:

(5.14)

Это свойство вытекает из определения f(x); производная неубывающей функции отрицательной быть не может.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

(5.15)

Это свойство следует из формулы (5.13), если положить в ней и учесть, что

Геометрически основные свойства (5.14) и (5.15) плотности f(x) интерпретируются как:

1) вся кривая распределения лежит не ниже оси абсцисс;

2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Выясним размерности функции распределения F(x) и плотности f(x). Функция распределения как всякая вероятность, размерности не имеет. Размерность плотности распределения обратна размерности случайной величины X.