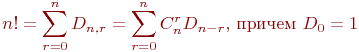Ответы на ТГ и МЛ :

№1. Множества и действия над ними

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Операции над множествами:

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).

№2. Законы Алгебры множеств

1. коммутативности:

2. ассоциативности:

3. дистрибутивности:

   • пересечения относительно объединения:

• объединение относительно пересечения:

4. идемпотентности:

5. действия с универсальным и пустым множествами:

6. де Моргана:

7. двойного дополнения:

№3. Отношения. Бинарные отношения

Виды отношений :

• унарные (n=0)

• бинарные (множество упорядоченных пар)

• координаты

Бинарным отношением между множествами и называется любое подмножество прямого произведения . Часто чтобы обозначить принадлежность упорядоченной пары к бинарному отношению вместо записи используют обозначения или . При этом говорят, что находится в отношении к . Если , то говорят, что задано на множестве .

Свойства:

• рефлексивности

• антирефлексивности

• симметричности

• антисимметричности

• транзитивности

• связанности

№4.Функции

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества.

Поведение функций:

• Сюръективность

• Инъективность

• Биективность

№5. Эквивалентные, конечные и бесконечные множества.

Множество A называется эквивалентным множеству B, если существует биекция f:А→B. В этом случае говорят также, что множество A имеет одинаковую мощность с множеством B. Обозначение:A~B или .

Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.

№6. Основные правила комбинаторики. Понятие выборки.

Правило суммы. Если некоторый объект А можно выбрать n способами, а другой B объект можно выбрать m способами, то выбор "либо A, либо B" можно осуществить n+m способами.

Правило произведения. Если объект A можно выбрать n способами, а после каждого такого выбора другой объект B можно выбрать (независимо от выбора объекта A) m способами, то пары объектов A и B можно выбрать n*m способами.

Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

№7. Размещения, сочетания и перестановки.

В комбинаторике размещением называется расположение «предметов» на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов некоторого n-элементного множества.

В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

В комбинаторике перестано́вка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве , которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки.

№8. Размещения и сочетания с повторениями. Примеры.

Размещение с повторениями или выборка с возвращением^[4] — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k равно:^[5][1][4]

Например, количество вариантов 3-x значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:

Пусть даны два натуральных числа n и k, k ≤ n. Пусть также у нас имеется набор предметов n различных сортов. Элементы одного сорта считаются одинаковыми, причем количество элементов одного сорта — неограниченно. Произвольный набор из k предметов называется сочетанием с повторениями из n элементов по k.

Пусть в коробке лежат шары трех цветов—красного, синего и зеленого. Шары одного цвета считаются одинаковыми. Вопрос: сколькими способами можно составить набор из двух шаров?   Число сочетаний с повторениями из n элементов по k обозначается ar{C}^k_n и равно C^k_n+k-1

№9. Сочетания и биномиальные коэффициенты. Пример.

Число сочетаний из n по k равно биномиальному коэффициенту

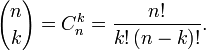
В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона (1 + x)ⁿ по степеням x. Коэффициент при x^k обозначается (иногда ) и читается «биномиальный коэффициент из n по k»

Пример . В турнире принимали участие n шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно в турнире?

.

№10. Размещения и перестановки без повторений. Примеры

Количество размещений из n по k, обозначаемое , равно убывающему факториалу:

Нужно выбрать президента общества, вице - президента, ученого - секретаря и казначея.Сколькими способами может быть сделан это выбор, если каждый член общества может занимать лишь один пост?

Перестановки без повторений - различные упорядочивания данного n-множества, отличающиеся друг от друга лишь порядком входящих в них элементов.

(от фр. "permutation" - перестановка)

Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга? . №11. Разбиения множеств на несколько частей. Полиномиальные коэффициенты. Пример.

Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.

Пусть X — произвольное множество. Семейство непустых множеств , где A — некоторое множество индексов (конечное или бесконечное), называется разбиением X, если:

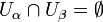1. для любых 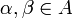, таких что ;

2. .

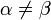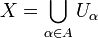Полиномиальный коэффициент - число способов размещения различных элементов по различным ячейкам, при котором в i-ю ячейку помещается n_i элементов, i=1, 2, . . ., m, без учета порядка элементов в любой ячейке.

№12. Формула включения-исключения

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.

Например, в случае двух множеств формула включений-исключений имеет вид:

В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы.

№13. «Задача о караванах», «Решето Эратосфена».

Задача о караванах:

 Рассмотрим еще одну задачу, в которой решение может быть получено с помощью главной теоремы комбинаторики, 9 верблюдов идут гуськом. Сколько существует комбинаций перестановки верблюдов, при которых ни один верблюд не идет за тем, за кем шел ранее.

   Выделим запрещенные пары: (1,2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9). Для решения применим главную теорему комбинаторики. Для этого определим, что есть объект и что есть свойства. Под объектами будем понимать различные расстановки верблюдов. Всего их будет N= 9!. Под свойствами будем понимать наличие определенной пары в перестановке. Таким образом число свойств равно 8, Тогда количество перестановок, не обладающих, ни одним из 8 свойств:

Решето Эратосфена:

этим именем называют следующий способ получения ряда простых чисел.

Из ряда чисел

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14...

вычеркивают кратные двум;

4, 6, 8, 10, 12,...

— кратные трем:

6, 9, 12, 15,...

— кратные пяти:

10, 15, 20, 25, 30,...

— кратные семи:

14, 21, 28, 35, 42, 49,...

и т. д.

Таким образом все составные числа будут просеяны, и останутся только простые числа 2, 3, 5, 7, 11, 13...

№14. Раскладка предметов на две кучки.

   Рассмотрим следующую задачу. Трое мальчиков собрали 40 яблок. Сколько имеется способов раздела яблок между ними?

    Напишем 40 единиц и 2 нуля, выполняющих как и ранее функции разделителя, и затем начнем их переставлять всеми возможными способами. Каждой перестановке будет соответствовать некоторый способ раздела 40 яблок на 3 кучки. Каждому способу раздела будет соответствовать некоторый код, содержащий 40 единиц и 2 нуля. Поэтому количество способов раздела:

Р(40, 2) = 42!/(2!40!) = 861.

№15.Задачи о смещениях.

 Число перестановок из элементов, при которых ни один элемент не остается в первоначальном положении:

 Число перестановок ,в которых ровно элементов остаются на месте ,а остальные меняют свое положение выражается формулой

В самом деле сначала нужно выбрать какие именно элементов остаются на месте. Это можно сделать способами , а остальные переставлять. Это можно сделать способами. По правилу произведения получаем .

 Сумма всех смещений равна

 Число перестановок из элементов, при которых данные элементов смещены (остальные могут быть смещены, а могут оставаться на своих местах), выражается формулой.

№16.Задачи на разбиения

n-первый предмет

m-второй предмет

P(m,n)=(m+n)!/m!n!

N одинаковый предметов можно разделить между k лицами :

k-1

P(n,k-1)=Cn+k-1

В частности если каждый должен получить не менее одного предмета:

k-1

Cn-1

№17. Формула Стирлинга

При k=n количество размещений равно количеству перестановок порядка n:

№18. Экспоненциальная производящая функция.

Экспоненциальная производящая функция последовательности {a_n} — это формальный степенной ряд

.

• Есл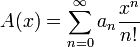и и 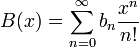— экспоненциальные производящие функции последовательностей {a_n} и {b_n}, то их произведение 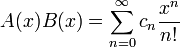является экспоненциальной производящей функцией последовательности

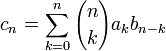
№19.Производящая функция и её свойства.

Производя́щая фу́нкция последовательности {a_n} — это формальный степенной ряд

.

Свойства

• Производящая функция суммы (или разности) двух последовательностей равна сумме (или разности) соответствующих производящих функций.

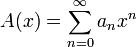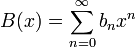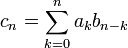• Произведение производящих функций и последовательностей {a_n} и {b_n} является производящей функцией свёртки этих последовательностей:

№20.Определение Графов и виды Графов.

Граф или неориентированный граф G — это упорядоченная пара G: = (V,E), для которой выполнены следующие условия:

• V это непустое множество вершин или узлов,

• E это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

Виды Графов: