16. Вывод координатного уравнения плоскости в пространстве.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Если плоскости π1: A1x + B1y + C1z + D1 = 0, π2: A2x+B2y+C2z+D2 = 0 не параллельны, то пересекаются по прямой. Точка M(x; y; z) принадлежит этой прямой тогда и только тогда, когда ее координаты удовлетворяют уравнению каждой из плоскостей, т.е. являются решениями системы уравнений

A1x + B1y + C1z + D1 = 0,

A2x + B2y + C2z + D2 = 0,

которую называют общими уравнениями прямой

Если a,b,c одновременно не равно 0, то уравнение ax+by+cz+d=0 задает в пространстве плоскость.

Возьмем какую-нибудь точку , координаты которой удовлетворяет уравнению.

ax+by+cz+d=0, если x,y,z=0 => d=0 (не имеет решения) (d не равно 0!!!)

( )

17)Док-во теоремы о расстоянии от точки до прямой (на плоскости). Смысл знака.

Док-во: Пусть B(x,y) - произ. прямой, тогда

Расстояние от точки до прямой

 

Теорема. Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

.

 

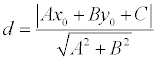Доказательство. Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁ :

 (1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

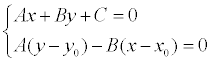
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x ₀ ) + B(y – y₀ ) + Ax₀ + By₀ + C = 0,

то, решая, получим:

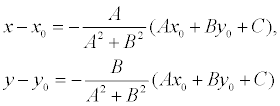
Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

18)Док-во теоремы о расстоянии от точки до плоскости (в пространстве).Смысл знака.

d=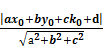 (наверное как и 17 вопрос)

19)Док-во теоремы об уравнении прямой в пространстве.

Пусть число отличны от 0. Тогда система задает в пространстве прямую, проходящую через точку и имеющую направляющий вектор с координатами

1- 2 уравнение и потом следствие от них

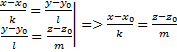
2- почему это прямая?

возьмем

=> система образует пересечение плоскостей.

и т.д. теорема доказана!

20)Определение прямой второго порядка.

Определение. Кривая на плоскости, задаваемая уравнением

(а11, а12, а22 одновременно не обращаются в ноль)

называется кривой второго порядка.

Примеры:

Пусть а,b>0

Анализ:

Модуль х ≤а

-а≤х≤а

Случай а=b ?

Окружность, R=а.

Эллипс-сжатие окружности

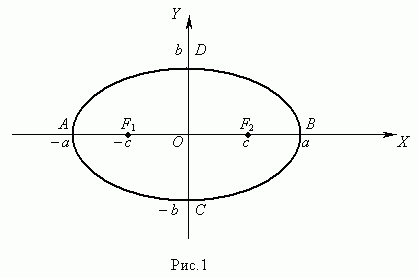
Пусть а,b>0

Парабола(нарисуйте сами(ветви вниз))

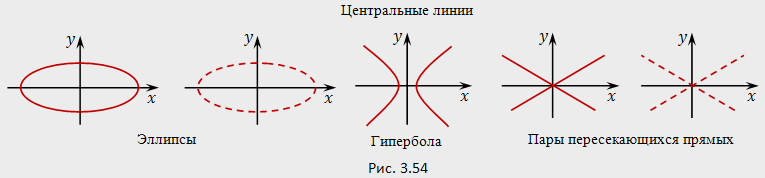
1)эллипс, 2) гипербола, 3) парабола, 4) -пара пересекающихся прямых

5) -пара параллельных прямых, 6) -точка,7) -мнимая окружность, 8) -пара совпадающих прямых-прямая

21)Определение аффинного преобразования плоскости. Примеры аффинных преобразований. Свойства аффинных преобразований.

Преобразованием плоскости называется произвольная биекция этой плоскости на себя. Преобразование плоскости называется аффинным ,если оно прямые переводит в прямые(и обратно).

Примеры: 1) тождественные преобразования (х,у)→(х,у), 2) (х,у)→(х+а,у+b) (а,b-фик-ые числа) а=1,b=2 (х-а,у-b)→(х,у)

(х,у)→( х+а,у+b)

(х1,у1)→(х1+а,у1+b)

На вектор (а,b)

3)(х,у)→(kx,ky),k≠0 – гомотетия

4) (х,у)→(kx,y),k≠0 – симметрия ОУ

5)поворот на фиксированный угол, поворот плоскости относительно точки на данный угол фи

6) косой сдвиг

Свойства аффинных преобразований

1. суперпозиция аффинных преобразований – аффинное преобразование

2. преобразование, обратное к аффинному, является аффинным

3. Запись аффинного преобразования в координатах