Рівень c
1
Змінити порядок інтегрування:
.
а)
;
2
Змінити порядок інтегрування:
.
б)
;
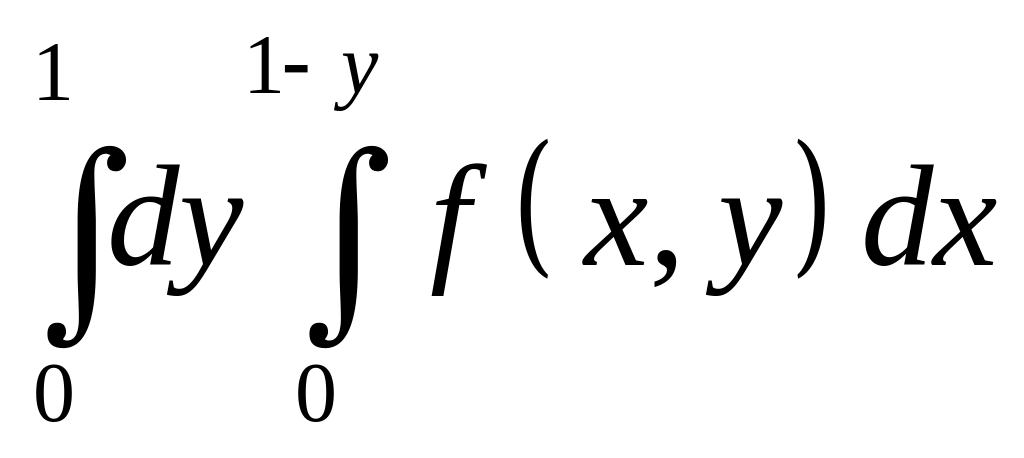3
Змінити порядок інтегрування:
.
б)
;
4
Змінити порядок інтегрування:
.
в)
;
5
Обчислити
,
якщо D
задана нерівностями:
.
в)
;
6
Обчислити
,
якщо D
задана нерівностями:
.
а)
;
7
Обчислити
,
якщо D
обмежена лініями
.
б)
;
8
Обчислити
,
якщо D
обмежена лініями
.
в)
;
9
Обчислити
,
якщо D
обмежена лініями
.
д) інша відповідь.
10
Обчислити
,
якщо D
обмежена лінією
.
в) 0;
11
Обчислити
,
якщо D
– прямокутник
.
в)
;
12
Обчислити
,
якщо D
– трикутник з вершинами О (0;0), А(1;0),
B(0;1).
б) ;
13 Обчислити , якщо D – трикутник з вершинами О (0;0), А(1;0), B(1;1).
а)
;
14 Обчислити , якщо D – трикутник з вершинами О (0;0), А(1;1), B(2;0).
а)
;
15 Обчислити , якщо D – паралелограм з вершинами А(-1;0), B(0;1), C(2;1), D(1;0).
в) 2;
16
Обчислити
,
якщо D
– прямокутник
.
в) 105;
17
Обчислити
,
якщо D
обмежена лініями
.
в)
;
18
Обчислити
,
якщо D
обмежена лініями
.
в)
;
19
Обчислити
,
якщо D
обмежена лініями
.
г) ;
20
Обчислити
,
якщо D
обмежена лініями
.
в)
;
21 Обчислити , якщо D обмежена лініями .
в)
;
22
Обчислити
,
якщо D
обмежена лініями
.
а) ;
23
Обчислити
,
якщо D
обмежена лініями
.
в)
;
24
Обчислити
,
якщо D
обмежена лініями
.
г)
;
25
Обчислити
,
якщо
задана нерівностями
.
а)
;
26
Обчислити
,
якщо
задана нерівностями
.
а)
;
27
Обчислити
,
якщо
задана нерівностями
.
б)
;
28
Обчислити
,
якщо
задана нерівностями
в)
;
29
Обчислити
,
якщо
задана нерівностями
.
д) інша відповідь.
30 Обчислити , якщо задана нерівностями .
б) ;
31
Обчислити
,
якщо
задана нерівностями
.
б)
;
32
Обчислити
,
якщо
задана нерівностями
.
в) ;
33
Обчислити
,
якщо
задана нерівностями
.
в)
;
34
Обчислити
,
якщо
задана нерівностями
.
а) ;
35
Обчислити
,
якщо
задана нерівностями
.
г)
;
36
Обчислити
,
якщо
задана нерівностями
.
д) інша відповідь.
37
Обчислити
,
якщо
задана нерівностями
.
б)
;
38 Обчислити , якщо задана нерівностями
.
а)
;
39
Обчислити
,
якщо
задана нерівностями
.
б)
;
40
Обчислити
,
якщо
задана нерівностями
.
б) ;
41
Обчислити
,
якщо
обмежена поверхнями
.
г) 7;
42
Обчислити
,
якщо
обмежена поверхнями
.
а) 12;
43
Обчислити
,
якщо
обмежена поверхнями
.
в) 8;
44
Обчислити
,
якщо
обмежена поверхнями
.
г) 25;
45
Обчислити
,
якщо
обмежена поверхнями
.
а) 32;
46
Обчислити
,
якщо
обмежена поверхнями
.
в) 16;
47
Обчислити
,
якщо
обмежена поверхнями
.
д) інша відповідь.
48
Обчислити
,
якщо
обмежена поверхнями
.
а) 0;
49 Обчислити , якщо обмежена поверхнями .
б) 0;
50
Обчислити
,
якщо
обмежена поверхнями
.
д) інша відповідь.
51
Обчислити
,
де АВ – відрізок прямої y=2x
від
точки А(0;0) до точки В(1;2).
б)
;
52
Обчислити
,
де АВ – відрізок прямої
від точки А(0;0) до точки В(2;1).
б)
;
53
Обчислити
,
де АВ – відрізок прямої
від
точки А(0;0) до точки В(1;4).
в)
;
54
Обчислити
,
де АВ – відрізок прямої
від
точки А(-4;-1) до точки В(8;2).
а)
;
55
Обчислити
,
де
– контур трикутника з вершинами О(0;0),
А(1;0),
В(0;1).
б) 1+
;
56 Обчислити , де – контур трикутника з вершинами О(0;0), А(2;0), В(1;1).
а)2+3 ;
57 Обчислити , де – контур трикутника з вершинами О(0;0), А(1;0), В(1;1).
в) 2+ ;
58 Обчислити , де – контур прямокутника з вершинами О(0;0), А(1;0), В(1;1), D(0;1).
а) 4;
59
Обчислити
, де
– арка циклоїди
,
0
.
б)
;
60
Обчислити
, де
– крива
,
0
.
г)
;
61
Обчислити
, де
– дуга гіперболи
.
а)
;
62
Обчислити
,
де
– частина кривої
від точки О(0;0;0)
до
точки А(3;3;2).
г) 5;
63
Обчислити
, де
– відрізок прямої, що з’єднує точки
А(-1;0)
і В(0;1).
б)
;
64
Обчислити
,
де
– дуга кривої
між точками
А(-1;0)
і В(1;0).
а) 6;
65
Обчислити
,
де
– відрізок прямої, що з’єднує точки
А(0;-2) і В(4;0).
б)
;
66 Обчислити , де – контур трикутника з вершинами А(-1;0), В(1;0), C(0;1).
д) інша відповідь.
67 Обчислити , де – контур прямокутника з вершинами А(0;0), В(4;0), C(4;2), D(0;2).
а) 24;
68
Обчислити
,
де
- чверть еліпса
.
а)
;
69
Обчислити
,
де
– дуга параболи
.
а)
;
70
Обчислити
,
де
– частина параболи
.
б)
;
71
Обчислити
,
де
– частина параболи
.
в)
;
72
Обчислити
,
де
– частина параболи
.
в)
;
73
Обчислити
,
де
– частина параболи
.
а) 3;
74 Обчислити , де – частина параболи .
г)
;
75
Обчислити
,
де
– частина параболи
.
г)
;
76
Обчислити
,
де
– верхня половина еліпса
,
яку
проходять за годинниковою стрілкою.
в)
;
77 Обчислити , де – нижня половина еліпса , яку проходять за годинниковою стрілкою.
б)
;
78
Обчислити
,
де
– контур трикутника, що обмежений осями
координат
і
прямою
,
який проходять проти годинникової
стрілки.
б) 2;
79
Обчислити
де
– контур трикутника, що обмежений осями
координат
і
прямою
,
який проходять проти годинникової
стрілки.
а)
;
80
Обчислити
,
де
– контур трикутника, що обмежений осями
координат
і
прямою
,
який проходять проти годинникової
стрілки.
в)
;
81
Обчислити
,
де
– контур трикутника, що обмежений осями
координат
і прямою
,
який проходять проти годинникової
стрілки.
б) -2;
82
Обчислити
,
де
– контур трикутника, що обмежений осями
координат
і прямою
,
який проходять проти годинникової
стрілки.
б) 2;
83
Обчислити
,
де
– дуга параболи
,
що знаходиться у
верхній
півплощині і яку проходять за годинниковою
стрілкою.
а)
;
84 Обчислити , де – ламана АВC, що з’єднує точки А(-2;0), В(0;4), C(2;0).
б)
;
85 Обчислити , де – відрізок прямої від точки А(-2;0) до точки B(2;0).
г) 0;
86
Обчислити
,
де
– дуга параболи
від точки А(0;0)
до
точки B(1;1).
а) 1;
87
Обчислити
,
де
– дуга параболи
від точки А(0;0)
до
точки B(1;1).
а) 1;
88 Обчислити , де – відрізок прямої від точки А(0;0) до точки B(1;1).
а) 1;
89
Обчислити
,
де
– відрізок прямої
від
точки А(0;0)
до
точки B(1;2).
в)
;
90
Обчислити
,
де
– дуга параболи
від
точки А(0;0)
до
точки B(1;2).
б)
;
91
Обчислити
,
де
– дуга параболи
від
точки А(0;0)
до
точки B(1;2).
д) інша відповідь.
92
Обчислити
,
де
– ламана АВC:
А(0;0),
В(2;0),
C(4;5).
б) 10,5;
93
Обчислити
,
де
– дуга параболи
від точки
А(-1;1)
до точки B(1;1).
г)
;
94
Обчислити
,
де
– дуга параболи
від точки
А(-1;2)
до точки B(1;2).
в)
;
95
Обчислити
,
де
– дуга кривої
від точки А(0;1)
до
точки B(-1;e).
а)
;
96
Обчислити
,
де
– дуга параболи
від точки А(0;0)
до
точки B(1;2).
б)
;
97
Обчислити
,
де
– дуга кривої
від точки А(1;0)
до
точки B(e;1).
в)
;
98
Обчислити
,
де
– дуга
синусоїди від точки А(
;0)
до точки В(0;0).
б)
;
99
Обчислити
,
де
– відрізок прямої від точки А(2;1)
до
точки В(1;2).
в)
;
100
Обчислити
,
де
– крива:
.
а) ;
101
Обчислити
,
де σ – поверхня частини площини x+2y+3z=6,
що розміщена в першому октанті.
а)
;
102
Обчислити
,
де σ – поверхня частини площини x+2y+3z=6,
що розміщена в першому октанті.
б)
;
103
Обчислити
,
де σ – частина бічної поверхні циліндра
,
що знаходиться в першому октанті.
в)
;
104
Обчислити
,
де σ – частина бічної поверхні циліндра
,
що знаходиться в першому октанті.
в)
;
105
Обчислити
,
де σ – частина бічної поверхні циліндра
,
що знаходиться в першому октанті.
г) ;
106
Обчислити
,
де σ – частина поверхні площини x+y+z=а,
що розміщена в першому октанті.
г)
;
107
Обчислити
,
де σ – частина поверхні площини x+y+z=а,
що розміщена в першому октанті.
а)
;
108
Обчислити
,
де σ – частина поверхні площини x+y+z=а,
що розміщена в першому октанті.
в)
;
109
Обчислити
,
де σ – частина поверхні площини x+y+z=а,
що розміщена в першому октанті.
в)
;
110
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
в) 2;
111
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
а) 0;
112
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
в) 2;
113
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
г) ;
114
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
г)
;
115
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
г) ;
116
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
а) 4;
117
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
б)
;
118
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
а) 4;
119
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
а) 4;
120
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
б) ;
121
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
г) 4;
122
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
в) 8;
123
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
б) 2
124
Обчислити
, де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
б) 2;
125
Обчислити
,
де σ –верхня сторона частини поверхні
,
що відтинається площинами
і розміщена в першому октанті.
г) ;
126
Обчислити площу
фігури, яка обмежена лініями:
.
б)
;
127
Обчислити площу
фігури, яка обмежена лініями:
.
б)8;
128
Обчислити площу
фігури, яка обмежена лініями:
.
а) 18;
129
Обчислити площу
фігури, яка обмежена лініями:
.
в) 2;
130
Обчислити площу
фігури, яка обмежена лініями:
.
а) 1;
131
Обчислити площу
фігури, яка обмежена лініями:
.
в) 1;
132
Обчислити площу
фігури, яка обмежена лініями:
.
в) 1;
133
Обчислити площу
фігури, яка обмежена лініями:
.
б)
;
134
Обчислити площу
фігури, яка обмежена лініями:
.
а)
;
135
Обчислити площу
фігури, яка обмежена лініями:
.
б)
;
136
Обчислити площу
фігури, яка обмежена лініями:
.
а)
;
137
Обчислити площу
фігури, яка обмежена лініями:
.
в) ;
138
Обчислити площу
фігури, яка обмежена лініями:
.
г)
;
139
Обчислити площу
фігури, яка обмежена лініями:
.
в)
;
140
Обчислити площу
фігури, яка обмежена лініями:
.
а)
;
141
Обчислити площу
фігури, яка обмежена лінією
.
в)
;
142
Обчислити площу
фігури, яка обмежена лініями:
.
г)
;
143
Обчислити площу
фігури, яка обмежена лініями:
.
б)
;
144
Обчислити площу
фігури, яка обмежена лінією
.
а) ;
145
Обчислити площу
фігури, яка обмежена лінією
.
а)
;
146
Обчислити площу
фігури, яка обмежена лінією
.
а)
;
147
Обчислити площу
фігури, яка обмежена лінією
.
г) 1;
148
Обчислити площу
фігури, яка обмежена заданою лінією:
.
а) 1;
149
Обчислити площу
фігури, яка обмежена лініями:
.
а)
;
150
Обчислити площу
фігури, яка обмежена лінією:
.
б) ;
151
Обчислити об’єм тіла,
обмеженого поверхнями:
.
г) ;
152
Обчислити об’єм тіла,
обмеженого поверхнями:
.
в) ;
153
Обчислити об’єм тіла,
обмеженого поверхнями:
.
а) 6;
154
Обчислити об’єм тіла,
обмеженого поверхнями:
.
б)
;
155
Обчислити об’єм тіла,
обмеженого поверхнями:
.
б) ;
156
Обчислити об’єм
тіла,
обмеженого поверхнями:
.
а) 45;
157
Обчислити об’єм тіла,
обмеженого поверхнями:
.
а)
;
158
Обчислити об’єм тіла,
обмеженого поверхнями
.
б)
;
159
Обчислити об’єм тіла,
обмеженого поверхнями
.
в)
;
160
Обчислити об’єм тіла,
обмеженого поверхнями
.
г) ;
161
Обчислити об’єм тіла,
обмеженого поверхнями
.
г)
;
162
Обчислити об’єм тіла,
обмеженого поверхнями
.
в)
;
163
Обчислити об’єм тіла,
обмеженого поверхнями
.
б)
;
164
Обчислити об’єм тіла,
обмеженого поверхнями
.
а)
;
165
Обчислити об’єм
тіла,
обмеженого поверхнями
.
а)
;
166
Обчислити об’єм тіла,
обмеженого поверхнями
.
д) інша відповідь.
167
Обчислити об’єм тіла,
обмеженого поверхнями
.
в) 1;
168
Обчислити об’єм тіла,
обмеженого поверхнями
.
а) 56;
169
Обчислити об’єм тіла,
обмеженого поверхнями
.
б) 2;
170
Обчислити об’єм тіла,
обмеженого поверхнями
.
г)
;
171
Обчислити об’єм тіла,
обмеженого поверхнями
.
а) 64;
172
Обчислити об’єм тіла,
обмеженого поверхнями
.
б)
;
173
Обчислити об’єм тіла,
обмеженого поверхнями
.
г)
;
174
Обчислити об’єм тіла,
обмеженого поверхнями
.
а) ;
175
Обчислити об’єм тіла,
обмеженого поверхнями
.
а)
;
176
Обчислити
масу пластини
,
яка обмежена лініями
,
якщо поверхнева густина визначається
функцією
.
а) ;
177
Знайти масу
пластинки. Пластинка
задана лініями, що її обмежують,
– поверхнева густина.
:
.
б) 5;
178
Знайти масу
пластинки. Пластинка
задана лініями, що її обмежують,
–
поверхнева густина.
:
.
в) 2,25;
179
Обчислити масу
тіла
,
яке обмежене поверхнями
і має густину
б)
;
180
Знайти статичний
момент
відносно осі абсцис однорідної пластинки
,
обмеженої кривою
,
та віссю
(густина
)
в)
;
181
Знайти статичний
момент прямокутника зі сторонами
та
відносно сторони
( поверхнева густина
).
а)
;
182
Знайти статичний
момент півкруга радіуса
відносно
діаметра (поверхнева густина
).
в)
;
183 Знайти центр ваги однорідної пластинки , обмеженої кривою , та віссю (поверхнева густина ).
а)
;
184
Знайти
координати центра ваги фігури, обмеженої
лініями
(поверхнева густина
).
а)
;
185
Знайти
момент
інерції відносно осі
однорідного тіла
(густина
),
обмеженого параболоїдом
і площиною
.
б)
;
186
Знайти момент
інерції однорідного тіла
(густина
),
обмеженого поверхнями
відносно осі
.
а)
;
187
Знайти момент
інерції однорідного тіла
(густина
),
обмеженого поверхнями
відносно осі
.
в)
;
188
Знайти довжину
дуги кривої, заданої рівнянням
.
а)
;
189
Знайти довжину
дуги кривої, заданої рівняннями
.
б)20;
190
Знайти довжину
дуги кривої, заданої рівнянням
.
а)
;
191
Знайти довжину
дуги кривої
.
б) ;
192
Знайти роботу
сили
при переміщенні вздовж лінії
від точки
до точки
:
,
–
відрізок прямої
,
.
б)24;
193
Знайти площу
частини площини
,
вирізаної координатними площинами.
в)
;
194
Обчислити потік
векторного поля
через зовнішню сторону замкненої
поверхні
.
;
.
г) ;
195
Знайти потік
векторного поля
через повну поверхню конуса
застосувавши формулу Остроградського.
а)
;
196
Знайти площу
частини площини
,
вирізаної координатними площинами.
в)
;
197
Задано векторне
поле
і площина
(
),
яка разом з координатними площинами
утворює піраміду V.
Нехай
–
основа піраміди, яка належить площині
(
);
– контур, який обмежує
,
– зовнішня нормаль до
.
Обчислити циркуляцію векторного поля
вздовж замкненого контура
,
застосувавши формулу Стокса до контура
і обмеженої ним поверхні
з нормаллю
.
г)
;
198
Задано векторне
поле
і площина
(
),
яка разом з координатними площинами
утворює піраміду V.
Нехай
–
основа піраміди, яка належить площині
(
);
L
– контур, який обмежує
,
– зовнішня нормаль до
.
Обчислити циркуляцію векторного поля
вздовж замкненого контура
,
застосувавши формулу Стокса до контура
і обмеженої ним поверхні
з нормаллю
.
в)1;
199
Обчислити
дивергенцію поля
в точці
.
а) 4;
200
Обчислити ротор
векторного поля
.
б) (2;2;2);