
Розділ 7 рівень b
1 Які з наведених нижче тверджень є правильними?
Обмеженість функції
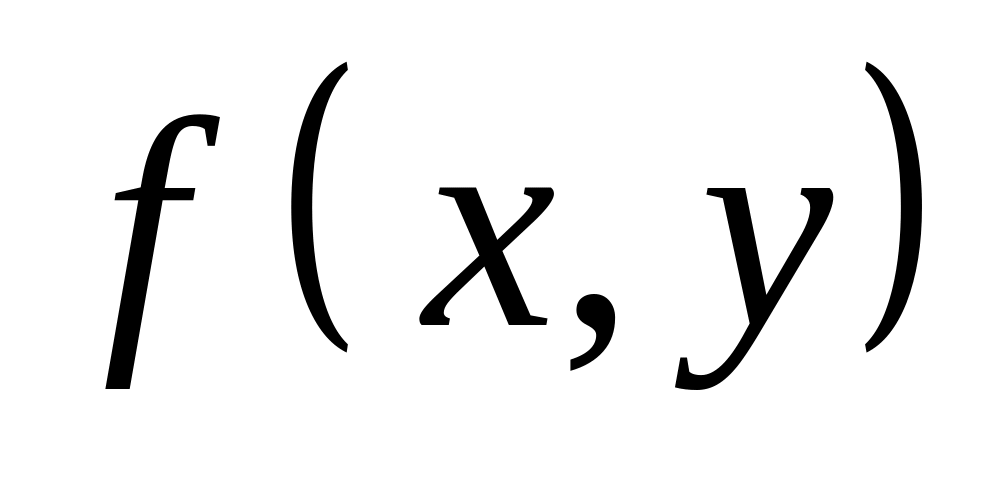 в обмеженій замкненій області
в обмеженій замкненій області
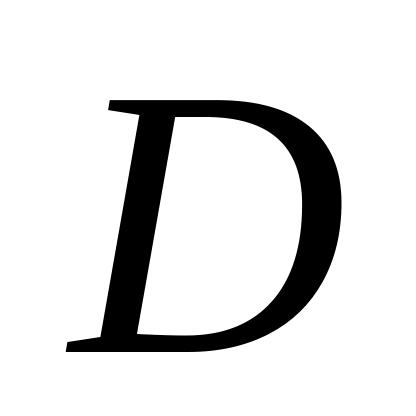 є достатньою умовою її інтегровності
в цій області.
є достатньою умовою її інтегровності
в цій області.
Неперервність функції в обмеженій замкненій області є достатньою умовою її інтегровності в цій області.
Обмеженість функції в обмеженій замкненій області є необхідною умовою її інтегровності в цій області.
Неперервність функції в обмеженій замкненій області є необхідною умовою її інтегровності в цій області.
б) 2 і 3;
2 Які з наведених нижче тверджень є правильними?
Якщо функція інтегровна в області , то вона неперервна в цій області.
Якщо функція інтегровна в обмеженій замкненій області , то вона обмежена в цій області.
Для того, щоб функція була інтегровною в області необхідно і достатньо, щоб область була обмеженою і замкненою, а функція – обмеженою в цій області.
Якщо функція неперервна в обмеженій замкненій області , то вона інтегровна в цій області.
в) 2 і 4
3 Які з наведених нижче тверджень не є правильними ?
1) Для того, щоб функція була інтегровною в області необхідно, щоб вона була неперервною в цій області.
2) Для того, щоб функція була інтегровною в області необхідно, щоб вона була обмеженою в цій області.
3) Для того, щоб функція була інтегровною в області достатньо, щоб вона була обмеженою в цій області.
4) Для того, щоб функція була інтегровною в області достатньо, щоб область була обмеженою і замкненою, а функція була неперервною в цій області.
в) 1 і 3;
4 Які з наведених нижче тверджень не є правильними ?
Для того, щоб функція була інтегровною в обмеженій замкненій області необхідно і достатньо, щоб функція була неперервною в цій області.
Для того, щоб функція була інтегровною в обмеженій замкненій області необхідно, щоб функція була обмеженою в цій області.
Для того, щоб функція була інтегровною в обмеженій замкненій області достатньо, щоб вона була неперервною в цій області.
Для того, щоб функція була інтегровною в обмеженій замкненій області достатньо, щоб вона була обмеженою в цій області.
а) 1 і 4;
5 Які з наведених нижче рівностей справедливі для подвійного інтеграла ?
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() (
(
![]() ).
).
г) 3 і 4;
6 Які з наведених нижче тверджень справедливі для подвійного інтеграла ?
Якщо в області функція
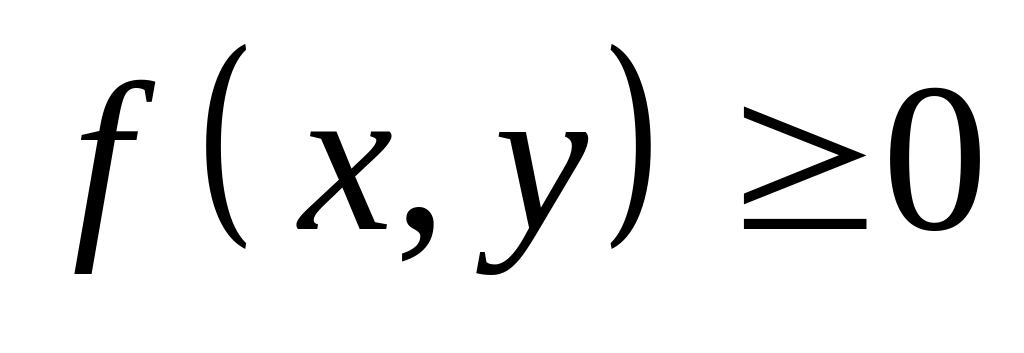 ,
то
,
то
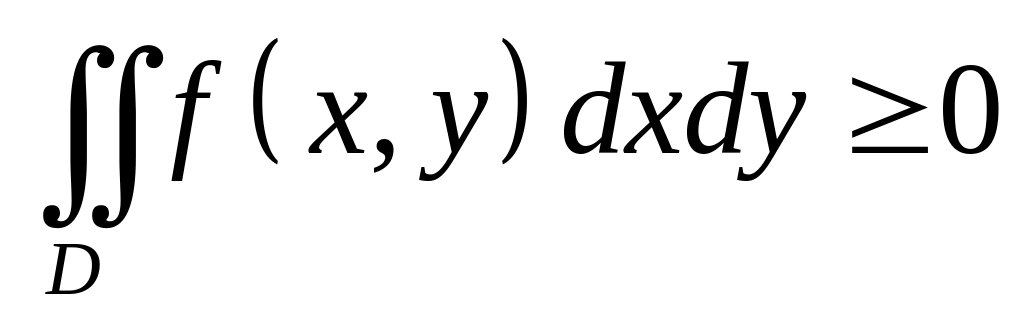 ;
;Якщо область
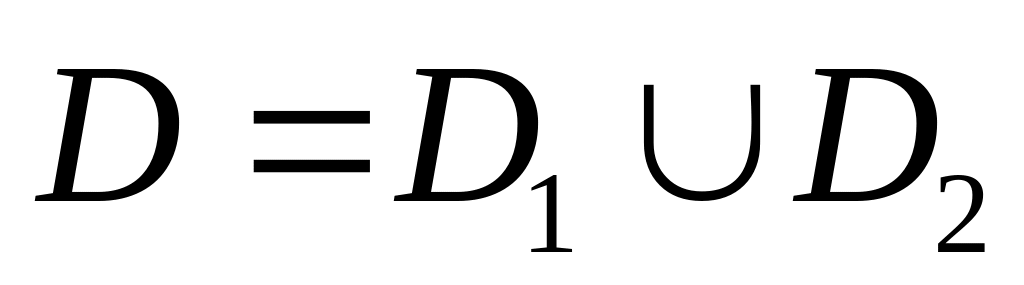 ,
причому
,
причому
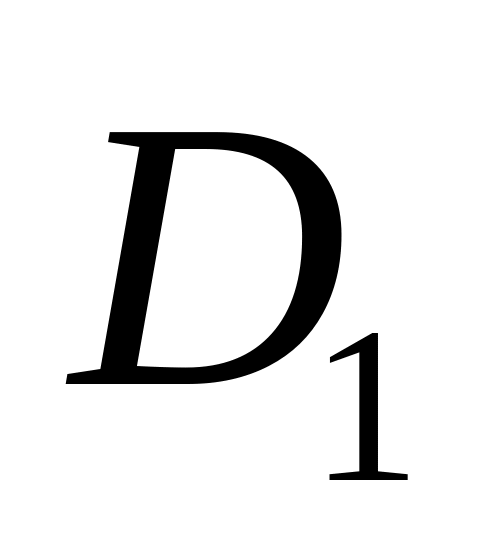 і
і
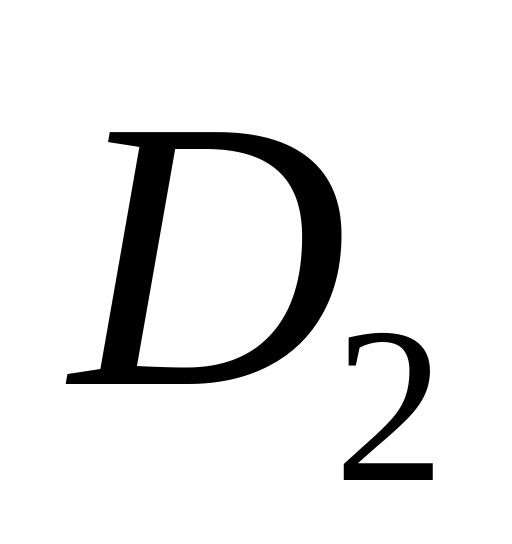 не мають спільних внутрішніх точок, то
не мають спільних внутрішніх точок, то
 ;
;Для довільних обмежених замкнених областей і справедлива рівність
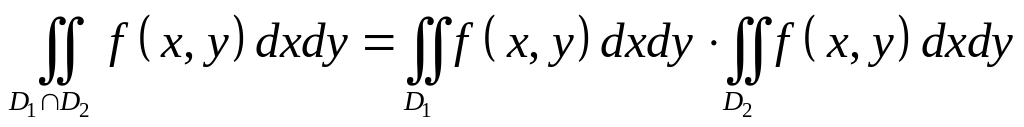 ;
;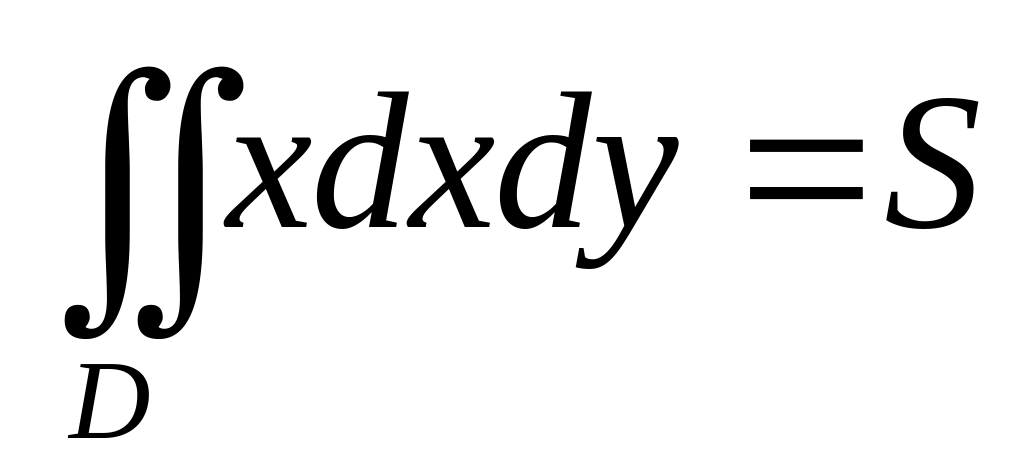 ,
де
,
де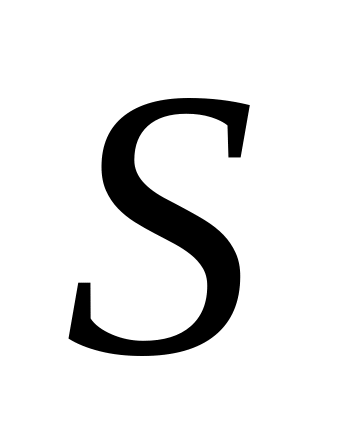 - площа області
.
- площа області
.
в) 1 і 2;
7
Якщо
![]() і
і
![]() - відповідно найменше і найбільше
значення функції
в області
,
а
- площа цієї області, то має місце оцінка
подвійного інтеграла:
- відповідно найменше і найбільше
значення функції
в області
,
а
- площа цієї області, то має місце оцінка
подвійного інтеграла:
б)
![]() ;
;
8 Середнім значенням функції в області називається величина ( - площа області ):
б)
![]() ;
;
9 За якою формулою можна обчислити площу плоскої фігури ?
г)
![]() ;
;
10 Які з наведених нижче формул не можуть бути правильними ?
1)
 ;
2)
;
2)
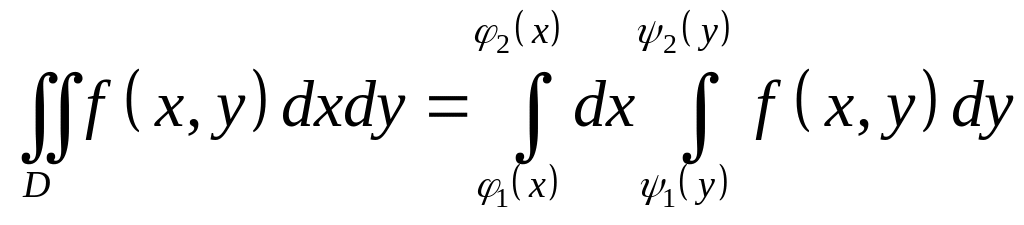 ;
;
3)
 ;
4)
;
4)
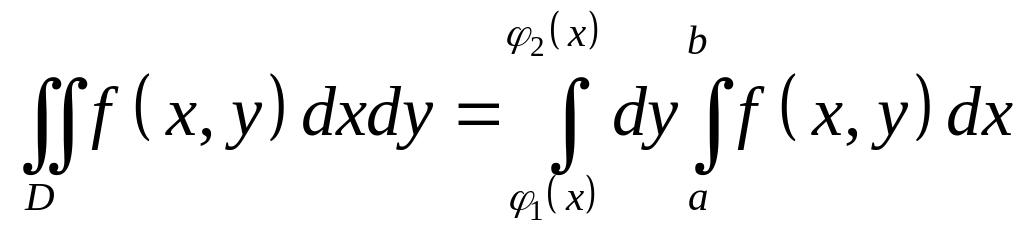 .
.
д) інша відповідь.
