5)Транспонирование

Матирица называется транспонированной к матрице А,если она получена из матрицы А заменой строк на столбцы

Теорема: =

Матрица называется обратной по отношению к матрице А,если *А=Е

№3 Определение минора элементы,алгебраического дополнения

Минором какого-либо элемента определителя,называется определитель,полученный из данного вычеркиванием той строки и того столбца,которым принадлежит этот элемент.

Минор элемента a_ik обозначается М_ik

Алгебраическим добавлением элемента a_ik называется его минор,взятый со знаком ,обозначение a_{ik =} *

Определитель равен сумме произведений элементов какой-либо его строки или столбца на их алгебраические добавления

№4 Понятие обратной матрице.Теорема об её вычислениях

Теорема:Пусть detA≠0,тогдаматрица А имеет обратную,она вычисляется по формуле =

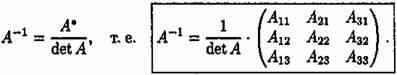
Пример решения смотрите в тетради

№5Понятие о Ранге матрицы

Ранг матрицы — наибольший порядок минора матрицы,отличного от нуля

Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы

Минор-определитель K-того порядка,составленный из элементов матрицы А,расположенных на пересечении выделенных строк и столбцов

Обычно ранг матрицы A обозначается rang A (rg A) или rank A. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.

Вычисление ранга матрицы

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Свойства

Теорема (о базисном миноре): Пусть r = rang A M — базисный минор матрицы A, тогда:

• базисные строки и базисные столбцы линейно независимы;

• любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).

 

Следствия:

• Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.

• Если A — квадратная матрица, и det A = 0 <=> строки и столбцы этой матрицы линейно зависимы.

• Пусть r = rang A, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

• Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны для матриц, полученных друг из друга

Теорема Кронекера — Капелли: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:{

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

№6 Системы линейных уравнений(СЛУ).Основные понятия

Системы 2х линейных уравнений с 2мя неизвестными

Определителем системы , называется число 𝚫 =│ а11 а12│

│а21 а22│

Введём дополнительные определители 𝚫х=│ │

│ │

𝚫 Y=│ │

│ │,числа а11,а22,а21,а22-коэф-ты системы

b1,b2-свободные члены

Если b1=b2=0,то система называется однородной,в противном случае не однородной

Пара чисел( ) называются решением системы,если она является решением каждого уравнения системы.

№7.СЛУ.методы решения

Формулы для нахождения решения системы: ; –формулы Крамера

Система не имеющая решения называется не совместной,если же система имеет хотя бы одно решение,её называют совместной

Возможны следующие случаи: 1)𝚫≠0,система имеет единственное решение,вычисляемое по формуле Крамера

2)𝚫=0,но хотя бы 1 из чисел 𝚫х,𝚫у отлично от 0,то система не совместна

3)𝚫=𝚫х=𝚫у=0,то система называется неопределённой и имеет бесконечно много решений

Методы решений:Метод Крамера,метод Гаусса,метод Обратной матрицы

№8.СЛУ.Метод Крамера

𝚫≠0,то единственное решение системы 1,определяется по формулам:

Пример

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

Если 𝚫=0,то возможны 2 случая:

*Если хотя бы 1 из определителей 𝚫х,𝚫у,𝚫z≠0,то система 1 не имеет решений

*Если 𝚫х=𝚫у=𝚫z=0,то системы имеют решение

В этом случае ищем связь между уравнениями системы:1)

𝚫=0;𝚫х=𝚫y=𝚫z=0

Если левую часть 1го уравнения умножить на 2,то получится левая часть второго уравнения ,однако правые части не дают такого результата,значит система не совместна. Ответ: нет решений

2)

При сложении первых двух уравнений получится 3е уравнение,значит его можно отбросить

𝚫=𝚫х=𝚫y=𝚫z=0=> ,Z=const =>

Находим определители,ответ.

№9.СЛУ.Метод Гаусса