
- •1. Множества и действия над ними.
- •2. Вещественные числа, их свойства.
- •3. Примеры счётных и несчётных множеств.
- •4. Предел последовательности и его едиственность.
- •5. Теоремы о существовании предела. Свойства пределов.
- •6. Теорема о пределе монотонной функции.
- •7. Бесконечно малые и бесконечно большие величины.
- •8. Блочное суммирование. Примеры.
- •9. Предел функции. Классификация разрывов.
- •10. Непрерывность сложной функции.
- •11. Теоремы о функциях, непрерывных на отрезке.
- •12. Равномерная непрерывность.
- •13. Производная. Касательная к кривой.
- •14. Правило дифференцирования сложной функции.
- •15. Замена переменной в неопределённом интеграле.
- •20. Функции с нулевой производной.
- •21. Первообразная. Формула Ньютона-Лейбница.
- •22. Производные высших порядков. Формула Тейлора.
- •23. Две теоремы о погрешности формулы Тейлора.
- •24. Пример гладкой функции с нулевыми многочленами Тейлора.
- •25. Исследование функций с помощью производных: монотонность, наибольшее и наименьшее значение, выпуклость, точки перегиба.
- •26. Экстремумы. Необходимые условия.
- •27. Экстремумы. Достаточные условия.
- •28. Приближённое решение уравнения методом итераций.
- •29. Дифференциал функции. Связь с приближёнными вычислениями.
- •30. Дифференцирование параметрически заданных функций.
12. Равномерная непрерывность.
Равномерная непрерывность – это свойство функции быть одинаково непрерывной во всех точках её области определения.
Функция называется равномерно непрерывной
на подмножестве M
X,
если
![]() <0
<0
![]() >0
>0
![]() Q(
Q(![]() Qy
Qy![]()
13. Производная. Касательная к кривой.
Производная функции y=f(x) в (.) х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
y’=limx→xo![]() ,
или
,
или
![]()
Касательной к данной кривой в данной точке М называется предельное положение МТ секущей МА, проходящей через точку М, когда вторая точка пересечения А неограниченно приближена по кривой к первой точке.
14. Правило дифференцирования сложной функции.
Пусть y=f(u) и u=v(x), тогда y=f(v(x)) – сложная функция с промежуточным аргументом u и независимым аргументом х.
Теорема: если функция u=v(x)
имеет производную u![]() в точке х, а функция y=f(u)
имеет производную y
в точке х, а функция y=f(u)
имеет производную y![]() в
соответствующей точке u=v(x),
то сложная функция y=f(v(x))
имеет производную y
в
точке х, которая находится по формуле
y
=
y
u
в
соответствующей точке u=v(x),
то сложная функция y=f(v(x))
имеет производную y
в
точке х, которая находится по формуле
y
=
y
u![]()
Доказательство. По условию
![]()
![]() .
Отсюда, по теореме о связи функции, её
предела и бесконечно малой, имеем:
.
Отсюда, по теореме о связи функции, её
предела и бесконечно малой, имеем:
![]() =
y
+а
где а→0 при
=
y
+а
где а→0 при
![]() →0,
или
→0,
или
![]() =
y
+а
. Функция u=v(x)
имеет производную в (.) х:
=
y
+а
. Функция u=v(x)
имеет производную в (.) х:
![]() ,
поэтому
,
поэтому
![]() u=
u=
![]()
![]() +b
,
где b→0 при
→0.
+b
,
где b→0 при
→0.
Подставив
u
в предыдущее равенство , имеем
![]() y
(
y
(
![]() +b
)+а(
+b
),
т.е.
+b
)+а(
+b
),
т.е.
y + y b +а +аb , разделив на и перейдя к пределу при →0, имеем y = y u
15. Замена переменной в неопределённом интеграле.
Если f(x)
непрерывна, то, полагая х=u(t),
где u(t)
непрерывна вместе со своей производной,
получаем
![]() =
=![]()
Таким образом, пусть требуется вычислить
интеграл
и удаётся найти функцию от х: t=u(x),
чтобы подынтегральное выражение
представилось в виде f(x)dx=g(u(x))u’(x)dx
– более удобная форма для интегрирования,
тогда достаточно найти интеграл
![]() ,
чтобы из него подстановкой получить
искомый интеграл.
,
чтобы из него подстановкой получить
искомый интеграл.
16. Теорема об обратной функции и её производной.
Производная обратной функции равна обратной величине производной данной функции.
y
=![]() ,
или
,
или
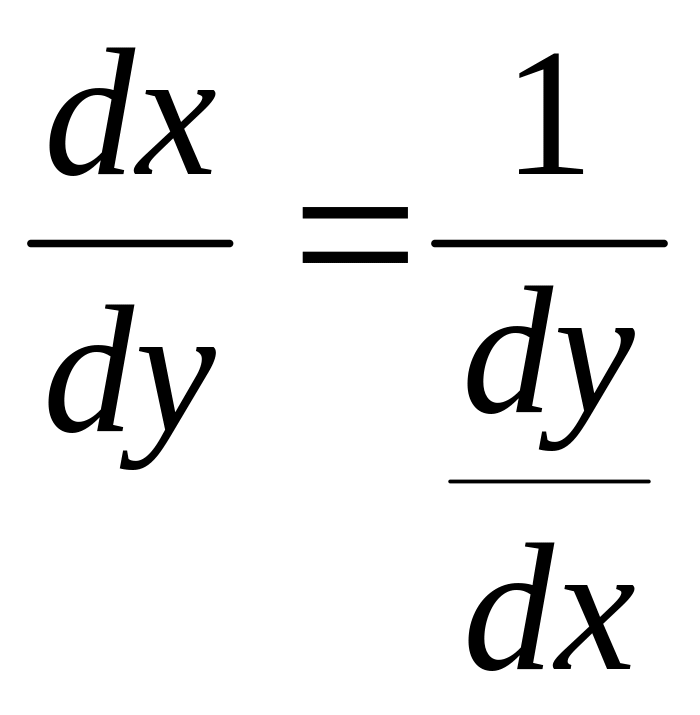
Рассмотрим обратную функцию x=u(y).
Дадим аргументу приращение
![]() .
Ему соответствует приращение Δх обратной
функции, причём
.
Ему соответствует приращение Δх обратной
функции, причём
![]() .
Поэтому
.
Поэтому
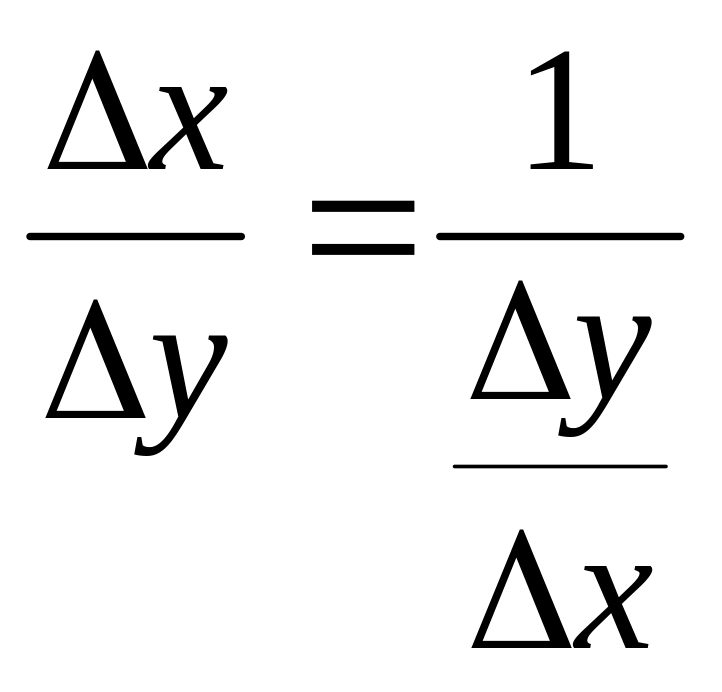
Если Δу→0, то в силу непрерывности
обратной функции приращение Δх!=0, и так
так
![]() ,
то
,
то
 ,
т. е. y
=
,
,
т. е. y
=
,
17. Дифференцирование произведения и интегрирование по частям.
(uv)’=u’v+v’u
Доказательство: Пусть y=uv.
Тогда y’=![]() =
=![]() =
=![]() =
=![]() =v(x)
=v(x)
![]() +
+
+u(x)
![]() +
+![]() =u’v+uv’+0u’=u’v+v’u
=u’v+uv’+0u’=u’v+v’u
Интегрирование по частям: Пусть u=u(x) и v=v(x) – функции , имеющие непрерывные производные. Тогда d(uv)=udv+vdu. Интегрируя это равенство, получим:
![]() =
=![]() ,
или
,
или
![]() =uv
-
=uv
-![]()
18.Дифференцирование и интегрирование рациональных функций.
19. Теоремы Ролля и Лагранжа. Правило Лопиталя.
Теорема Ролля
Пусть 1)функция f(x) определена и непрерывна в замкнутом промежутке [a;b]; 2)существует конечная производная f’(x), по крайней мере, в открытом промежутке (a;b), 3)на концах функция принимает равные значения. Тогда между a и b найдётся такая (.) с, что f’(c)=0
Доказательство:
f(x) непрерывна в замкнутом промежутке, значит по теореме Вейерштрасса принимает в этом промежутке наибольшее М и наименьшее m значения. 1)если M=m, то f(x) в промежутке сохраняет постоянное значение, а тк (const)’=0, то f(x)=0. 2) M>m. Оба эти значения достигаются, причём на разных концах промежутка, значит хоть одно из них достигается в (.) с. Тогда, по теореме Ферма (о равенстве производной нулю в точке наибольшего (наименьшего) значения), f’(c)=0.
Теорема Лагранжа
Пусть 1) )функция f(x)
определена и непрерывна в замкнутом
промежутке [a;b];
2)существует конечная производная f’(x),
по крайней мере, в открытом промежутке
(a;b). Тогда
между a и b
найдётся (.) с, такая, что
![]() .
.
Доказательство:
Введём вспомогательную функцию:
F(x)=f(x)-
![]() (x-a)
(x-a)
Эта функция удовлетворяет всем условиям теоремы Ролля (она непрерывна, т.к. является разностью непрерывной и линейной функции. В промежутке (a,b) она имеет определённую конечную производную: F’(x)=f’(x)- и принимает равные значения на концах промежутка: F(a)=F(b)=0). Следовательно, к функции можно применить теорему Ролля: F’(c)=0. Таким образом, f(c)- =0, или f(с)= .
Правило Лопиталя
Если f(x)=y(x)=0
или f(x)=y(x)=![]() ,
то
,
то
![]() =
=![]() =а
=а
Доказательство (по теореме Коши):
![]()
![]()
![]() ,
x→a=>c→a=>
,
x→a=>c→a=>![]() =
=![]()
