Ограниченные множества, их грани. Теорема о существовании граней.

Пусть Е- произвольное числовое множество, .

Определение 1. Число 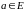называется наименьшим (наибольшим) элементом множества Е, если выполняется 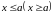. Если Е имеет наибольший (наименьший) элемент, то он .

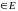Определение 2. Множество Е называется ограниченным сверху, если 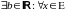выполнено .

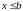Определение 3. Число b называется верхней границей множества Е, если .

Очевидно, что если b- верхняя граница множества Е, то любое число, большее b, также будет верхней границей множества Е. Таким образом ограниченное сверху множество имеет множество верхних границ.

Определение 4. Множество Е называется ограниченным снизу, если 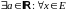выполнено .

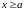Число а называется нижней границей множества Е.

Определение 5. Множество Е неограниченно сверху, если .

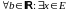
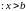Определение 6. Множество Е неограниченно снизу, если : .

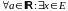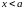Определение 7. Множество Е называется ограниченным, если оно ограничено и сверху, и снизу, то есть 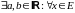выполнено .

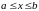Определение 7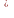 . Множество Е называется ограниченным, если 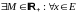выполнено .

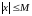Определение 8. Множество 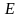называется неограниченным, если : .

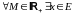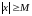Определение 9. Верхней гранью множества Е (или точной верхней границей множества Е) называется наименьшая из всех верхних границ множества Е. Обозначается 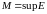(супремум) или

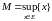
Определение 10. Нижней гранью множества Е (или точной нижней границей множества Е) называется наибольшая из всех нижних границ множества Е.

Обозначается m=infE (инфимум) или .

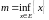infE может как принадлежать так и не принадлежать множеству E.

Теорема. Всякое ограниченное сверху непустое множество имеет верхнюю грань. Всякое ограниченное снизу непустое множество имеет нижнюю грань.

Доказательство.

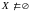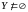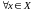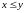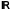
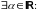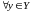Пусть – ограничено сверху. Пусть Y – множество чисел, ограничивающих сверху множество Х. Так как Х ограничено сверху, то . Так как каждый элемент ограничивает сверху множество Х , то выполняется . Тогда в силу непрерывности множества и выполняется .

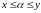Неравенство 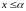означает, что a ограничивает сверху множество Х, то есть является верхней границей.

Неравенство 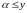означает, что a- наименьшая из верхних границ (так как Y- множество верхних границ) .

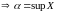Предел последовательности. Первое свойство пределов последовательностей, выражаемое неравенствами.

Пусть дана последовательность : (1)

Определение 1. Число а называется пределом последовательности , если 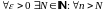выполнено (2)

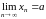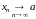Обозначается: или или .

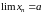Если последовательность имеет предел а, то она называется сходящейся к а.

Если последовательность не имеет предела, то она называется расходящейся.

Определение 2. Последовательность называется сходящейся, если 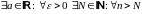выполнено .

Неравенство (2) равносильно неравенству 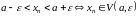. Следовательно, определение предела последовательности можно сформулировать в терминах окрестностей.

Определение 3. Число а называется пределом последовательности , если .

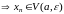ТУТ СВОЙСТВА КОТОРЫХ НЕ НАШЕЛ

Арифметические свойства пределов последовательностей.

Теорема 2. 1)Пусть ,

2) , .

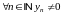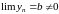Тогда .

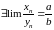Некоторые известные пределы: 1. 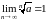, где a>0. 2. .

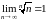II. В теоремах 1 и 2 предполагалось, что последовательности (x_n) и (y_n) имеют конечные пределы и, кроме того, в теорем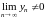е 2 . Теперь рассмотрим случай, когда последовательности могут быть, ББП, а в теореме 2 - БМП.

1. Частное .

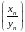1) , .

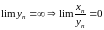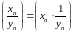- БМП, так как - сходящаяся, а -БМП.

2) , .

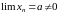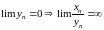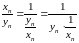. Последовательность - БМ, так как

- БМП, а 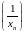- сходящаяся, значит, 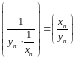- ББП.

3) , .

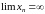, - сходящаяся последовательность, - БМП.

Значит, БМП. Следовательно, - ББП.

4) , (аналогично).

5) .

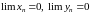Рассмотрим примеры:

а) ,

б) ,

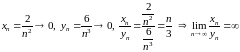в) ,

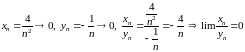г) 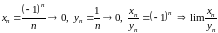не .

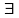В этом случае имеем отношение двух БМП. Это отношение может иметь предел (конечный или бесконечный), а может и не иметь предела в зависимости от конкретного способа задания последовательностей и . Поэтому отношение двух БМП называется неопределенностью вида .

Если предел отношения найден или доказано, что он не существует, то говорят, что неопределенность раскрыта.

6)

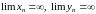
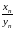- отношение двух ББП – неопределенность вида

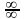
2. Сумма .

1) , ,

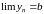
2) , ,

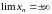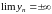
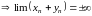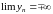
3) , 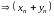- неопределенность вида .

3. Произведение .

1) , ,

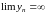
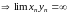2) , ,

3) , - неопределенность вида .

Существуют еще другие виды неопределенностей, связанные со степенями.

Ограниченные последовательности. Теорема об ограниченности сходящейся последовательности.

Теорема 2. (Необходимое условие сходимости) Всякая сходящаяся последовательность ограничена.

Доказательство.

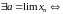
Пусть сходящаяся последовательность, то есть выполнено .

1. .

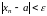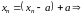
Значит, 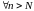выполнено .

Обозначим М=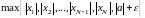 . Тогда "n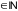 выполнено 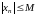, то есть (по определению) последовательность ограничена.

Замечание. Обратное утверждение неверно. Последовательность может быть ограничена, но не иметь предела.

Следствие. Если последовательность не ограничена, то она расходится.

(доказательство от противного)

Монотонные последовательности. Теорема о пределе монотонной последовательности.

Определение 1. Верхней гранью последовательности называется верхняя грань множества значений элементов этой последовательности.

Обозначается .

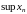Если множество значений элементов последовательности ограничено сверху, то есть число: 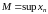Если множество значений неограниченно сверху, то .

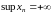Определение. 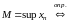1¢. 1) ,

2) .

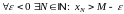Определение 2. Нижней гранью последовательности называется нижняя грань множества значений этой последовательности.

Обозначается inf x_n.

Если множество значений элементов последовательности ограничено снизу, то . Если множество значений не ограничено снизу, то .

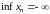Определение 2¢. 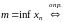1) ,

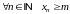2) .

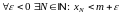Теорема 1. 1) Любая неубывающая, ограниченная сверху последовательность имеет конечный предел.

2) Любая невозрастающая, ограниченная снизу последовательность имеет конечный предел.

Доказательство.

1) - ограниченная сверху .

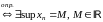Докажем, что .

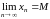Выберем 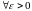. Тогда по определению 1' для этого e выполняется два условия:

1) ,

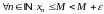2)

Так как - неубывающая, то .

Следовательно, выполнены условия 1) и 2), значит, выполнено 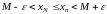. Т. е. Þ .

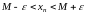
Итак, 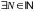: выполняется .

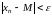
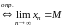Заметим, что из условия 1) следует, что .

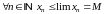2) Доказывается аналогично.

Устанавливается, что 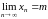и, следовательно, .

Теорема 2. 1) Всякая неубывающая, неограниченная сверху последовательность имеет .

2) Всякая невозрастающая, неограниченная снизу последовательность имеет .

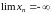Доказательство.

1) неограниченная сверху ,

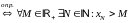неубывающая или Þ .

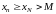Т.о. .

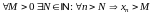
2) Доказывается аналогично, причем .

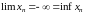Теорема о вложенных отрезках. Случай стягивающихся отрезков.

Пусть дана последовательность отрезков

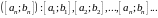a_n<b_n

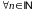
Определение 1. Последовательность отрезков называется последовательностью вложенных отрезков, если

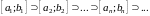, (1)

то есть каждый последующий отрезок содержится в предыдущем.

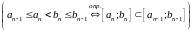
Определение 2. Последовательность вложенных отрезков называется стягивающейся, если длины этих отрезков стремятся к нулю при возрастании n, то есть если .

Теорема. (принцип вложенных отрезков).

Для любой стягивающейся последовательности вложенных отрезков существует единственная точка с, принадлежащая всем отрезкам этой последовательности, то есть такая, что .
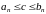