
- •Матрицы и действия с ними
- •Определители n-ого порядка. Методы вычисления.
- •Обратная матрица и методы её нахождения.
- •Критерий существования обратной матрицы
- •Ранг матрицы и методы его нахождения.
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
- •Теорема о ранге матрицы
- •Теорема о базисном миноре
- •Системы линейных уравнений: определение, общее решение, частное решение. Метод Крамера.
- •Решение системы линейных уравнений при помощи обратной матрицы
- •Метод Гаусса.
- •Теорема Кронекера-Капелли.
- •Однородные системы. Фундаментальная система решений.
- •Вектор. Линейные операции над векторами и их свойства.
- •Проекция вектора на ось. Направляющие косинусы вектора.
- •Линейная зависимость системы векторов. Основные теоремы о линейной зависимости системы 3-х,(4-х) векторов.
- •Понятие базиса. Разложение вектора по базису. Ортонормированные базисы. Размерность.
- •Скалярное произведение и его свойства. Условие ортогональности.
- •Векторное произведение и его свойства. Условие коллинеарности. Геометрический смысл векторной производной.
- •Смешанное произведение и его свойства. Условие компланарности векторов. Геометрический смысл смешанного произведения.
- •Декартова система координат. Перенос начала, поворот. Полярная система координат.
- •Прямая на плоскости. Общее уравнение.
- •Каноническое и параметрическое уравнение прямой.
- •Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условие параллельности и перпендикулярности прямых.
- •Уравнение прямой проходящей через 2 точки. Уравнение прямой в отрезках.
- •Расстояние от точки до прямой.
- •Расположение прямых на плоскости.
- •Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках.
- •Расстояние от точки до плоскости.
- •Угол между плоскостями. Расположение плоскостей.
- •Уравнение плоскости проходящей через данную точку перпендикулярно данному направлению. Уравнение плоскости проходящей через 3 точки.
- •Прямая в пространстве. Каноническое и параметрическое уравнение прямой.
- •Прямая как пересечение двух плоскостей. Приведение к каноническому виду
- •Расстояние от точки до прямой в пространстве.
- •Расстояние между прямыми в пространстве.
- •Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью.
- •Пересечение прямой и плоскости. Проекция точки на прямую и плоскость.
- •Гипербола
- •Парабола
- •Директрисы эллипса и гиперболы.
Уравнение прямой проходящей через 2 точки. Уравнение прямой в отрезках.
Уравнение прямой, проходящей
через две точки: A(x1, y1)
и B(x2, y2),
записывается так: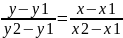
![]()
Угловой коэффициент прямой,
проходящей через две данные точки,
определяется по формуле: k
=

Уравнение прямой в отрезках:
ax+by+c=0, c 0
ax+by= -c
 +
+ = 1
= 1
 +
+
 = 1
= 1
 +
+
 = 1, где А, В – количество единичных
отрезков отсекаемых прямой от оси ОХ и
ОУ соответственно.
= 1, где А, В – количество единичных
отрезков отсекаемых прямой от оси ОХ и
ОУ соответственно.
Расстояние от точки до прямой.
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую. Если точка M0∈l , то ρ(M0,l)=0 (расстояние от точки M0 до прямой l) Для всякой точки M2 M1 M0M2>M0M1
Найдем ρ(M0,l) -
?
O − прямоугольная
система координат;
− прямоугольная
система координат;
M0(x0,y0);M1(x1,y1);
 ⊥
l и
⊥
l и  ⊥
l ;
⊥
l ;
∣∣ , тогда · =∣ ∣ ·∣ ∣(±1)
(x1−x0,y1−y0); (A,B);
· =A(x1−x0)+B(y1−y0)=Ax1+By1−(Ax0+By0), т.к. M1(x1,y1)∈l⇒Ax1+By1+C=0 , следовательно, последнее выражение можно переписать в виде: · =A(x1−x0)+B(y1−y0)=−(С+Ax0+By0)
Длина
вектора ∣
∣=
Подставим все в выражение (1): −(С+Ax0+By0)=±ρ(M0,l)
Откуда
получим конечное
выражение для нахождения расстояния
от точки до прямой:
ρ(M0,l)
=

Расположение прямых на плоскости.
Пусть l1: A1x+B1y+C1=0 и l2: A2x+B2y+C2=0 – общие уравнения двух прямых на координатной плоскости Оху. Тогда
1) если ![]() ,
то прямые l1 и l2 совпадают;
,
то прямые l1 и l2 совпадают;
2) если ![]() ,
то прямые l1 и l2 параллельные;
,
то прямые l1 и l2 параллельные;
3) если ![]() ,
то прямые l1 и l2 пересекаются.
,
то прямые l1 и l2 пересекаются.
4) если А1А2+В1В2=0, то прямые l1 и l2 перпендикулярны
5) углом между прямыми, будет угол между
их нормальными векторами: cos
=
Пусть l1: и l2:
и l2: - канонические уравнения двух прямых
- канонические уравнения двух прямых
 ,
то прямые l1 и l2 параллельные;
,
то прямые l1 и l2 параллельные;m1m2+n1n2=0, то прямые l1 и l2 перпендикулярны;
углом между прямыми, будет угол между их направляющими векторами: cos =

Пусть l1: y=k1x+b1, k1=tg 1 и l2: y=k2 x+b2, k2=tg 2
tg =
 - угол между прямыми l1 и l2,
где поворот от l1 и l2 происходит
против часовой стрелки;
- угол между прямыми l1 и l2,
где поворот от l1 и l2 происходит
против часовой стрелки;k2=k1, то прямые l1 и l2 параллельные;
k1= -
 , то прямые l1 и l2
перпендикулярны.
, то прямые l1 и l2
перпендикулярны.
Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках.
Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0
где А, В, С – координаты вектора -вектор нормали к плоскости.
Уравнение называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Если
в уравнении плоскости
Ax + By + Cz + D =
0 ни
один из коэффициентов A,
B,
C не
равен нулю, то это уравнение может быть
преобразовано к виду
 -
уравнение
плоскости «в отрезках».
-
уравнение
плоскости «в отрезках».
Где a
= -
 ,b
= -
,b
= -
 ,
c
= -
,
c
= -
 суть
величины отрезков, которые плоскость
отсекает на координатных осях (считая
каждый от начала координат).
суть
величины отрезков, которые плоскость
отсекает на координатных осях (считая
каждый от начала координат).
