
Поле в диэлектрике.
Для потенциального электрического поля
(rot E = 0)
соотношением E = –grad![]() вводится
скалярная расчетная величина
(потенциал), как любой скаляр
удовлетворяет тождеству rot grad
≡ 0,
при этом
вводится
скалярная расчетная величина
(потенциал), как любой скаляр
удовлетворяет тождеству rot grad
≡ 0,
при этом
![]() ,
где C – константа.
,
где C – константа.
Электрический потенциал точки A
![]() ,
где P – точка, потенциал
которой принят (задан) равным нулю:
,
где P – точка, потенциал
которой принят (задан) равным нулю:
![]() .
.
Разность электрических потенциалов
точек A и B
(электрическое напряжение
![]() )
)
![]() .
.
Выражения градиента потенциала в декартовых, цилиндрических и сферических координатах:
Декартовы (x, y и z) |
|
Цилиндрические (r, α и z) |
|
Сферические (r, θ и α) |
|
В декартовой системе координат
![]() ,
,
![]() ,
,
![]() .
.
В однородной среде (ε=const)
для потенциала справедливо уравнение
Пуассона:
![]() .
.
Решением уравнения Пуассона является
выражение:![]() ,
где V – объем, занятый
свободными зарядами, распределенными
с плотностью ρ; r –расстояние
от точки определения потенциала до
точки расположения элементарного заряда
,
где V – объем, занятый
свободными зарядами, распределенными
с плотностью ρ; r –расстояние
от точки определения потенциала до
точки расположения элементарного заряда
![]() .
.
В областях, не занятых объемными
зарядами (ρ=0) имеет место частный
вид уравнения Пуассона – уравнение
Лапласа:
![]() .
.
Выражения Δφ в декартовых, цилиндрических и сферических координатах:
Декартовы (x, y и z) |
|
Цилиндрические (r, α и z) |
|
Сферические (r, θ и φ) |
|
Граничные условия.
Для нахождения потенциала φ уравнение Пуассона (Лапласа) следует дополнить граничными условиями:
На поверхности проводника |
На границе раздела двух сред 1 и 2 с диэлектрическими проницаемостями ε1 и ε2 |
где
|
где
– составляющая вектора напряженности
поля, касательная к границе раздела
сред, т.е.
|
где
|
где
Для связанного заряда:
|
Емкость проводящих тел.
Емкость уединенного проводящего тела
определяется отношением
![]() ,
,
где q – заряд тела, φ – его потенциал, определенный при условии, что потенциал бесконечно удаленной точки принят равным нулю: φ∞ = 0.
Емкость между двумя уединенными
проводящими телами (конденсаторная
емкость) равна отношению:
![]() ,
где q1 – заряд
первого тела; φ1
и φ 2 – потенциалы
тел, определенные при условии, что
q2 = –q1.
Для однородной двухпроводной линии
длиной
,
где q1 – заряд
первого тела; φ1
и φ 2 – потенциалы
тел, определенные при условии, что
q2 = –q1.
Для однородной двухпроводной линии
длиной
![]() ,
кабеля длиной
вводится емкость на единицу длины
,
кабеля длиной
вводится емкость на единицу длины
![]() [Ф/м].
[Ф/м].
Задача 1. Плоский конденсатор с двумя слоями диэлектрика d1 = d2=1 см;
εrl = 3, εr2 = 6 (рис. 1) зарядили до напряжения U = 100 В и отключили от источника. Найти электрическое смещение, напряженность поля и распределение потенциала в обоих диэлектриках.
Определить: 1) как изменятся эти величины и емкость конденсатора, если из конденсатора вынуть пластину второго диэлектрика; 2) каковы будут эти величины, если конденсатор останется подключенным к источнику.

Рис. 1
Решение.
Напряжение между
пластинами конденсатора (разность
потенциалов):
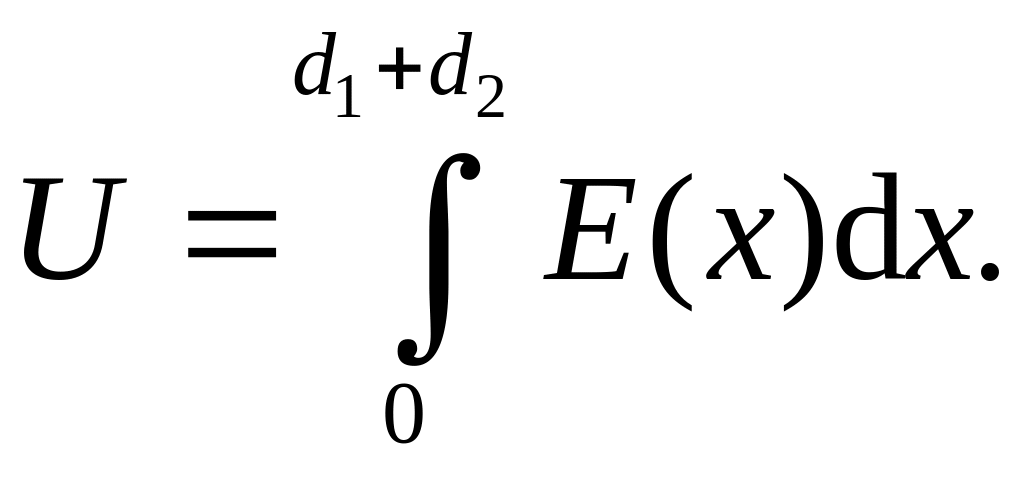 В пределах каждого диэлектрика
напряженность
поля постоянна, поэтому U
= E1d1
+ E2d2.
На границе двух
диэлектриков свободный заряд
отсутствует и, следовательно, по εr1E1
= εr2E2.
В пределах каждого диэлектрика
напряженность
поля постоянна, поэтому U
= E1d1
+ E2d2.
На границе двух
диэлектриков свободный заряд
отсутствует и, следовательно, по εr1E1
= εr2E2.
Следовательно, напряженность в каждом слое:
![]()
Электрическое смещение:
D1 = D2 = D = εr1ε0E = 200 ε0 = 17,72·10-12 Кл/см2.
Потенциал
![]() ,
следовательно, с учетом
,
следовательно, с учетом
![]() и
и
![]() ,
,
φ1 = (100 – 66,7х) В и φ2 = (66,7 – 33,3х) В, где х - в сантиметрах.
1) Если вынуть вторую
пластину при отключенном источнике,
то останется неизменным заряд на
пластинах, поверхностная
плотность которого по (13.19) равна
электрическому смещению,
т.е. останется
прежним: σ=D=
17,72![]() 10-12
Кл/см2.
10-12
Кл/см2.
Напряженность поля по при εr2 = 1: Е1 = D/ εr1ε0 = 66,7 В/см; Е2 = D/ εr2 ε0 = 200 В/см;
Напряжение на конденсаторе увеличится: U = E1d1 + E2d2 = 266,6 B.
Распределение потенциала: φ1 = (266,6 – 66,7х); φ2 = (400 – 200х) В.
2) Если вынуть пластину второго диэлектрика при включенном источнике, то напряжение останется прежним, и при εr2 = 1 получим:
![]()
Электрическое смещение D = εr1ε0E1 = εr2ε0E2 = 6,65 10-12 Кл/см2, т.е. плотность заряда на пластинах уменьшится.
Распределение потенциала: φ1 = (100 – 25х) В и φ2 = (150 – 75х) В.
В обоих случаях емкость конденсатора на единицу поверхности электродов
С0 = q/U = D/U = εr1εr2ε0/(d1εr2 + d2εr1) уменьшится.
Задача 2. В пространстве между
заземленными электродами плоского
воздушного конденсатора распределен
электрический заряд плотностью ρ,
равной ρ = ax. Координата x
отсчитывается по нормали от одного из
электродов. Найти потенциал и напряженность
поля. Расстояние между электродами
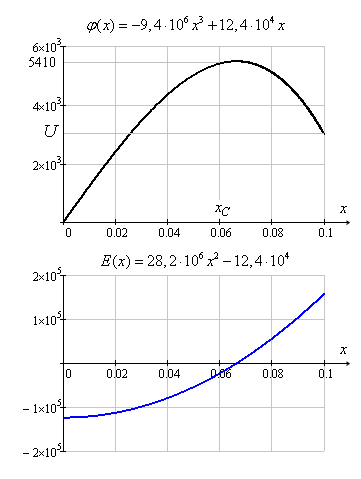
равно 2d. Построить распределение
![]() ,
,
![]() ,
найти потенциал
,
найти потенциал
![]() изолированной металлической сетки,
удаленной на расстоянии
изолированной металлической сетки,
удаленной на расстоянии
![]() от левой заземленной пластины. Пластина
расположена строго параллельно пластинам.
от левой заземленной пластины. Пластина
расположена строго параллельно пластинам.
Дано: d= 0,1 м, а=5·10-4 Кл/м3, U=3 кВ, =6 см.
Решение. В области 0 < x < d
(Рис. 1) потенциал удовлетворяет
уравнению Пуассона
![]() .
При интегрировании
.
При интегрировании
![]() ,
,
![]() .
.
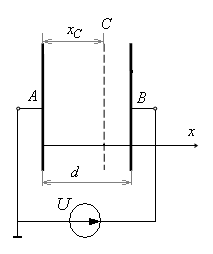
Рис. 1
Константы С1 и С2
(постоянные интегрирования) найдем из
заданных граничных условий (заданных
значений потенциалов)
![]() и
и
![]() .
После подстановки С2=0,
.
После подстановки С2=0,
![]() имеем С1=12,4·104 В/м,
окончательно
имеем С1=12,4·104 В/м,
окончательно
![]() (В).
(В).
Так как
,
то
![]() (В/м).
(В/м).
Потенциал сетки
![]() В.
В.
Задача 3. Решить задачу 2 при условии, что сетка заземлена, а источник изолирован.
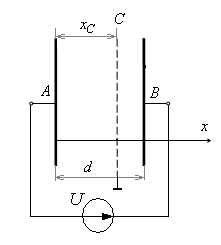
Решение. Общий вид решения не
изменится, но константы С1 и
С2 (постоянные интегрирования)
найдем из заданных граничных условий
заданных значений потенциала
![]() и разности потенциалов
и разности потенциалов
![]() .
Получим
.
Получим
![]() (В). Левый и правый электрод будут иметь
потенциалы
(В). Левый и правый электрод будут иметь
потенциалы
![]() В,
В,
![]() В.
В.

Так как , то распределение не изменится.
Коаксиальный кабель представляет
собой симметричную систему проводников
(жила и оболочка) с диэлектрической
прослойкой (изоляция между жилой и
оболочкой) и может быть рассмотрен как
цилиндрический конденсатор. Поле кабеля
является плоскопараллельным, распределение
потенциала во всех параллельных
плоскостях, нормальных к осевой
координате, является одинаковым. На
основе теоремы Гаусса при однородной
изоляции между жилой и оболочкой и
равномерном распределении заряда по
поверхности жилы можем записать, что
![]() ,
где
,
где
![]() -
линейная плотность заряда,
-
линейная плотность заряда,
![]() -
расстояние, отсчитываемое от центра
(оси),
-
расстояние, отсчитываемое от центра
(оси),
![]() ,
,
![]() - радиус жилы,
- радиус жилы,
![]() -
внутренний радиус оболочки. Модуль
вектора напряженности выражается
равенством
-
внутренний радиус оболочки. Модуль
вектора напряженности выражается
равенством
![]() [В/м]. При
[В/м]. При
![]() Гауссова поверхность не охватывает
неподвижного свободного заряда, поэтому
электростатического поля внутри
проводника нет и
Гауссова поверхность не охватывает
неподвижного свободного заряда, поэтому
электростатического поля внутри
проводника нет и
![]() .
При
.
При
![]() суммарный охваченный поверхностью
заряд равен нулю и
.
Напряжение между жилой и оболочкой
может быть найдено по формуле
суммарный охваченный поверхностью
заряд равен нулю и
.
Напряжение между жилой и оболочкой
может быть найдено по формуле
![]() [В],
[В],
Электрическая емкость на единицу длины
коаксиального кабеля:
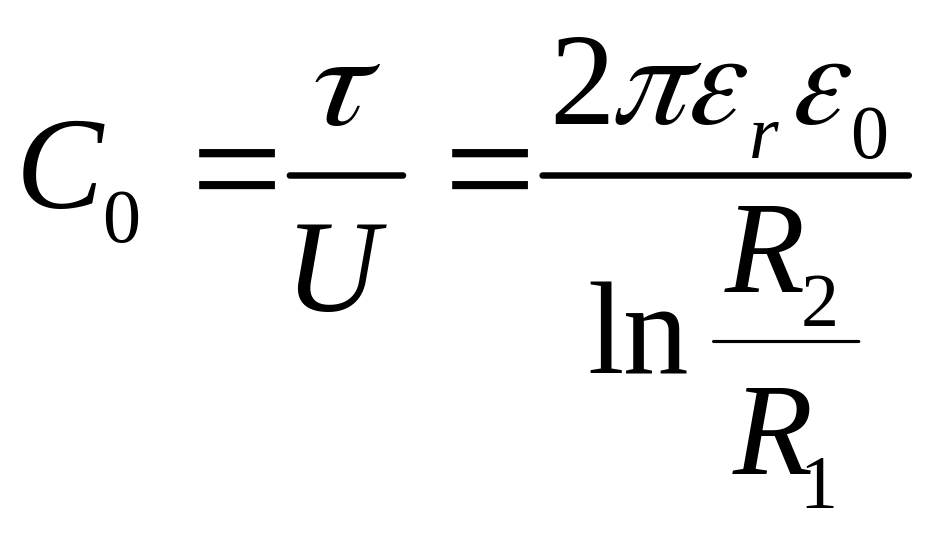 [Ф/м].
[Ф/м].
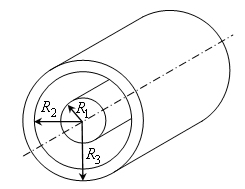
Максимальная напряженность, как следует
из зависимости
![]() ,
наблюдается в точке, расположенной на
поверхности жилы при
,
наблюдается в точке, расположенной на
поверхности жилы при
![]() ,
таким образом
,
таким образом
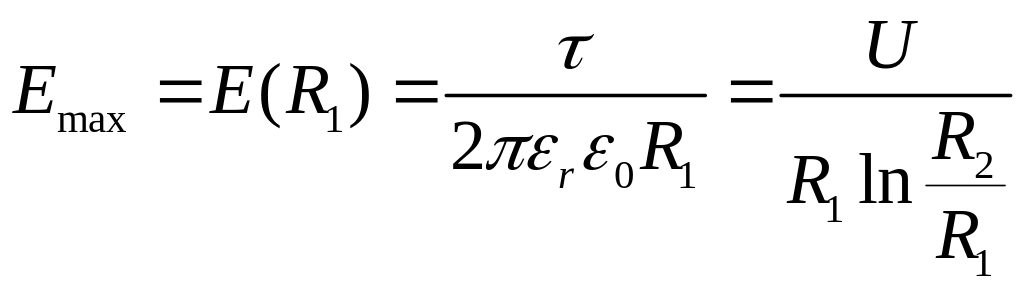 .
Максимальная напряженность не должна
превышать допустимую напряженность
изоляции1
Emax
.
Максимальная напряженность не должна
превышать допустимую напряженность
изоляции1
Emax![]() Eдоп;
максимально допустимое напряжение
может быть определено из условия
Eдоп;
максимально допустимое напряжение
может быть определено из условия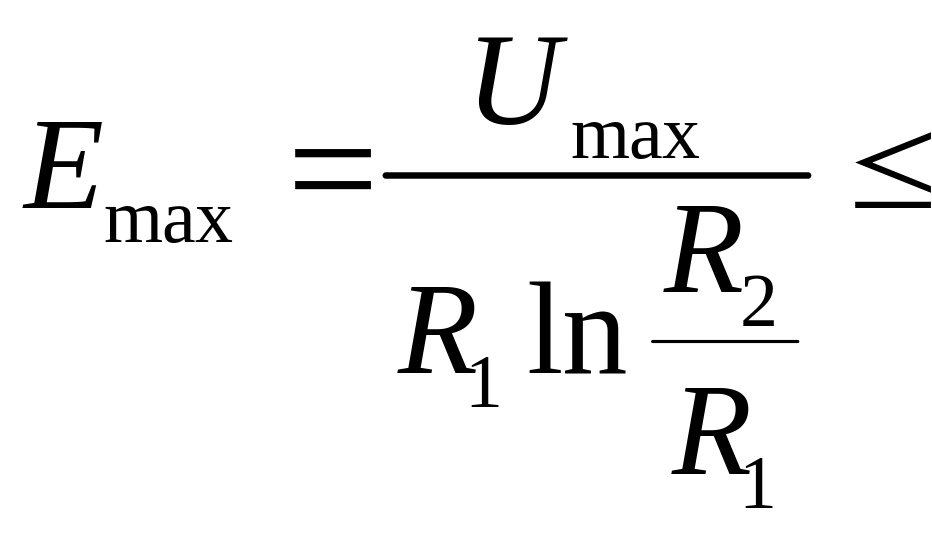 Eдоп.
Следовательно,
Eдоп.
Следовательно,
Umax=
Eдоп![]() .
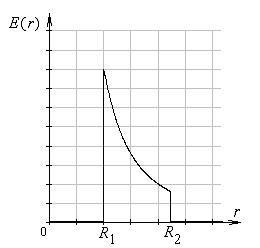
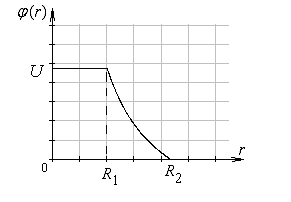
Графики
и
.
Графики
и
![]() при
при
![]() имеют вид:
имеют вид:
Задача 4. К цилиндрическому конденсатору дважды подводится напряжение, доводящее конденсатор до пробоя: первый раз, когда диэлектриком был воздух, пробивная напряженность которого Епр = E1 =30 кВ/см, и второй раз, когда диэлектриком было масло (εr = 2,4) с Епр = Е2 = 54 кВ/см.
Определить соотношение между напряжениями, прикладываемыми к конденсатору в первом и во втором случаях, и между зарядами конденсаторов в тех же случаях.
Решение.
По теореме Гаусса напряженность поля
в изоляции
цилиндрического конденсатора
![]() .
Учитывая, что разность
потенциалов или напряжение
.
Учитывая, что разность
потенциалов или напряжение
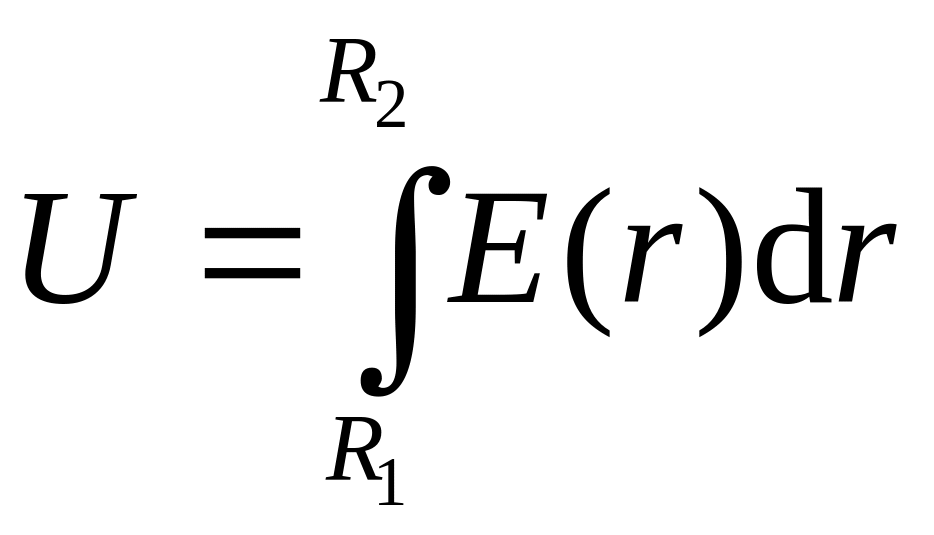 ,
получим
,
получим
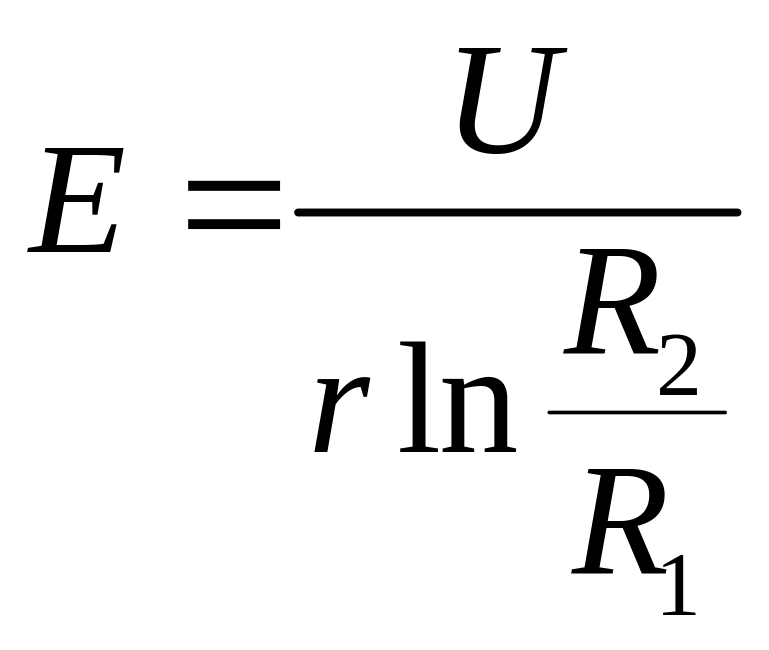 ,
где R1
- радиус внутреннего проводника
(жилы) и R2
— внутренний
радиус внешнего проводника (оболочки),
.
,
где R1
- радиус внутреннего проводника
(жилы) и R2
— внутренний
радиус внешнего проводника (оболочки),
.
Максимальная напряженность поля на поверхности жилы при :
![]()
откуда допустимое
напряжение при
![]() равно
равно
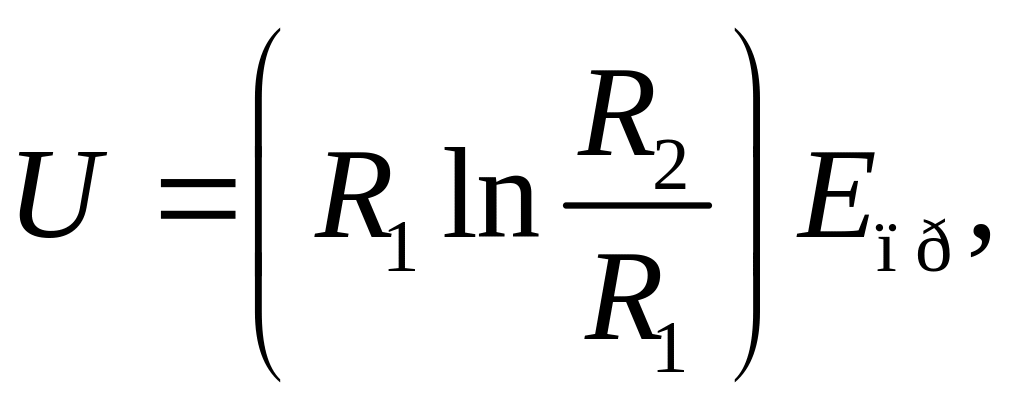
и максимальный заряд на единицу длины τ = 2πεrε0R1Eпр.
Следовательно, отношение допустимых напряжений равно отношению пробивных напряженностей: U1/U2 = Е1/ Е2 = 0,556, а отношение зарядов τ1/τ2 = Е1/εrE2 = 0,232.
Задача 5. Цилиндрический конденсатор (рис.2), где R1 = 1 мм, R2 =2 мм, R3 = 4 мм) заполнен двухслойным диэлектриком: 1) εra = 1; εrb = 3 или
2) εra = 3; εrb = 1.
О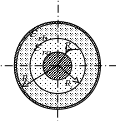 пределить
в обоих случаях пробивное напряжение
и построить
зависимости напряженности поля от
радиуса. Сравнить
со случаем однородного диэлектрика,
имеющего свойства слоя
а или
b.
пределить
в обоих случаях пробивное напряжение
и построить
зависимости напряженности поля от
радиуса. Сравнить
со случаем однородного диэлектрика,
имеющего свойства слоя
а или
b.
Рис. 2
Пробивная напряженность воздуха 30 кВ/см, пробивная напряженность диэлектрика 60 кВ/см.
Решение.
Из теоремы Гаусса следует, что![]() для
и
для
и
![]() для
для![]() .
Напряжение между
жилой и оболочкой:
.
Напряжение между
жилой и оболочкой:
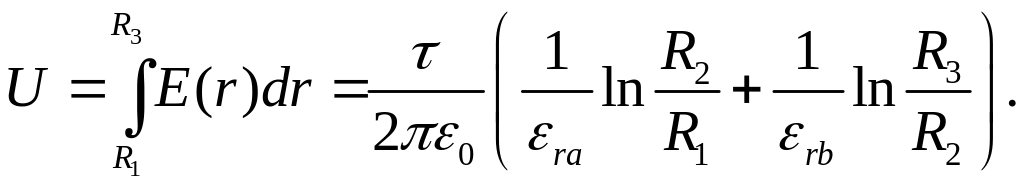
В случае 1, если допустить Еmax = Ea max при r = R1, то τ = 6πε0, если Еmax = Eb max при
r = R2, то τ = 72πε0.
Во избежание пробоя надо взять меньшее значение заряда, т.е. τ = 6πε0, при этом пробивное напряжение:
![]()
В случае 2 меньшее значение τ = 12πε0 и пробивное напряжение
![]()
Из зависимостей Е(r) видно, что в случае 2 поле в конденсаторе меньше изменяется, что приводит к повышению пробивного напряжения.

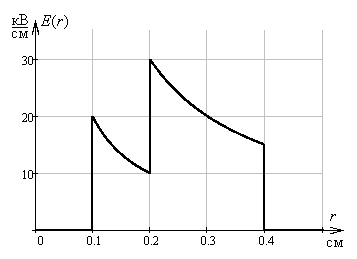
1) 2)
Если изоляция
конденсатора заполнена только диэлектриком
εra
= 1,
то есть Ea
max
= 30 кВ/см = τ/2πεrа
ε0R1,
тогда τ = 6πε0.
При этом![]() .
Если изоляция
конденсатора заполнена только диэлектриком
εrb
= 3, то Eb
max
= 60 кВ/см = τ/2π
εrb
ε0
R1
и τ
= 36πε0,
при этом
.
Если изоляция
конденсатора заполнена только диэлектриком
εrb
= 3, то Eb
max
= 60 кВ/см = τ/2π
εrb
ε0
R1
и τ
= 36πε0,
при этом
![]()
1 Допустимая напряженность Eдоп или Eпроб для воздуха Eдоп=30 кВ/см, твердого диэлектрика
Eдоп=60![]() 200
кВ/см, масла Eдоп=54
кВ/см.
200
кВ/см, масла Eдоп=54
кВ/см.
