
Коническая поверхность пересекается по эллипсу плоскостью …

|
|
|
|
ПО КАКОЙ КРИВОЙ ПЕРЕСЕКАЕТ ПЛОСКОСТЬ ПОВЕРХНОСТЬ КОНУС???
Тема: Пересечение поверхностей
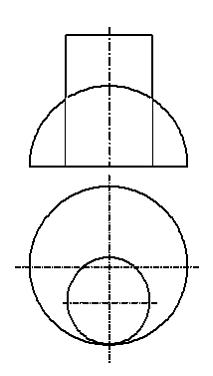
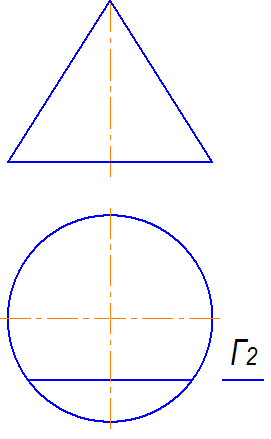
Линия
пересечения заданных на чертеже цилиндра
и сферы на горизонтальной плоскости
проекций совпадет с …
|
|
|
проекцией цилиндра |
|
|
|
проекцией сферы |
|
|
|
осевыми линиями |
|
|
|
проекциями цилиндра и сферы |
Решение: Если одна из пересекающихся поверхностей проецирующая, то задача построения линии пересечения двух поверхностей упрощается и сводится к построению недостающих проекций кривой линии на второй, не проецирующей поверхности. В данном примере горизонтальная проекция линии пересечения цилиндра и сферы совпадет с горизонтальной проекцией цилиндра.
Метод сфер
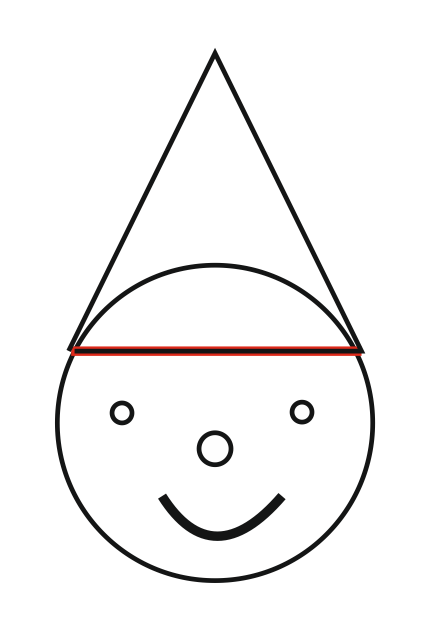
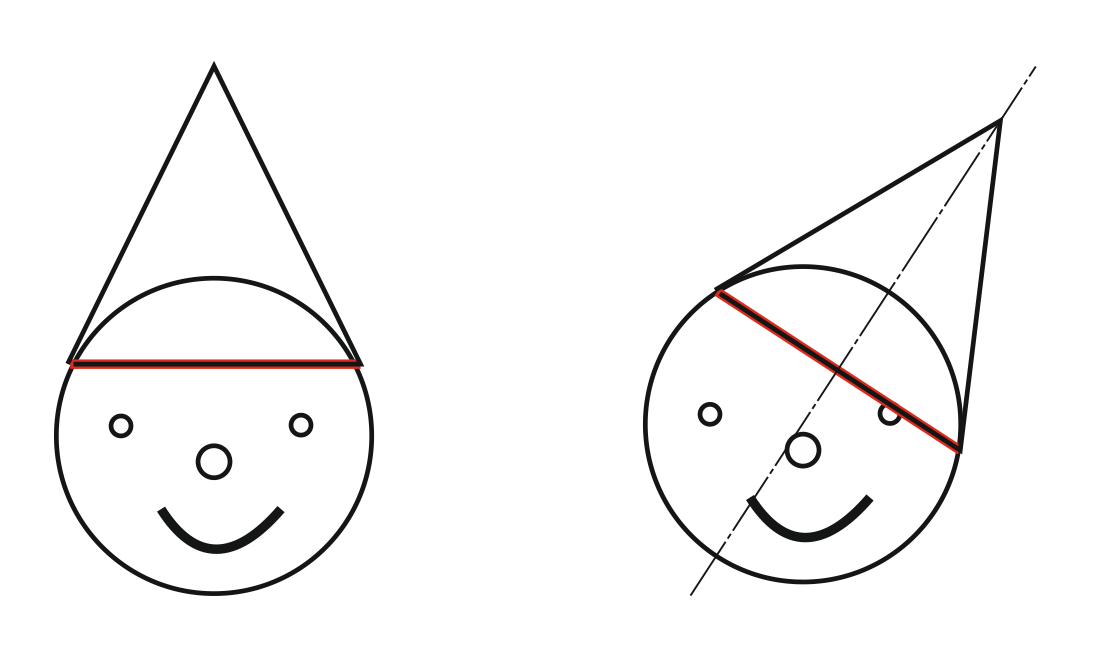
Две соосные поверхности вращения пересекаются по ОКРУЖНОСТИ …
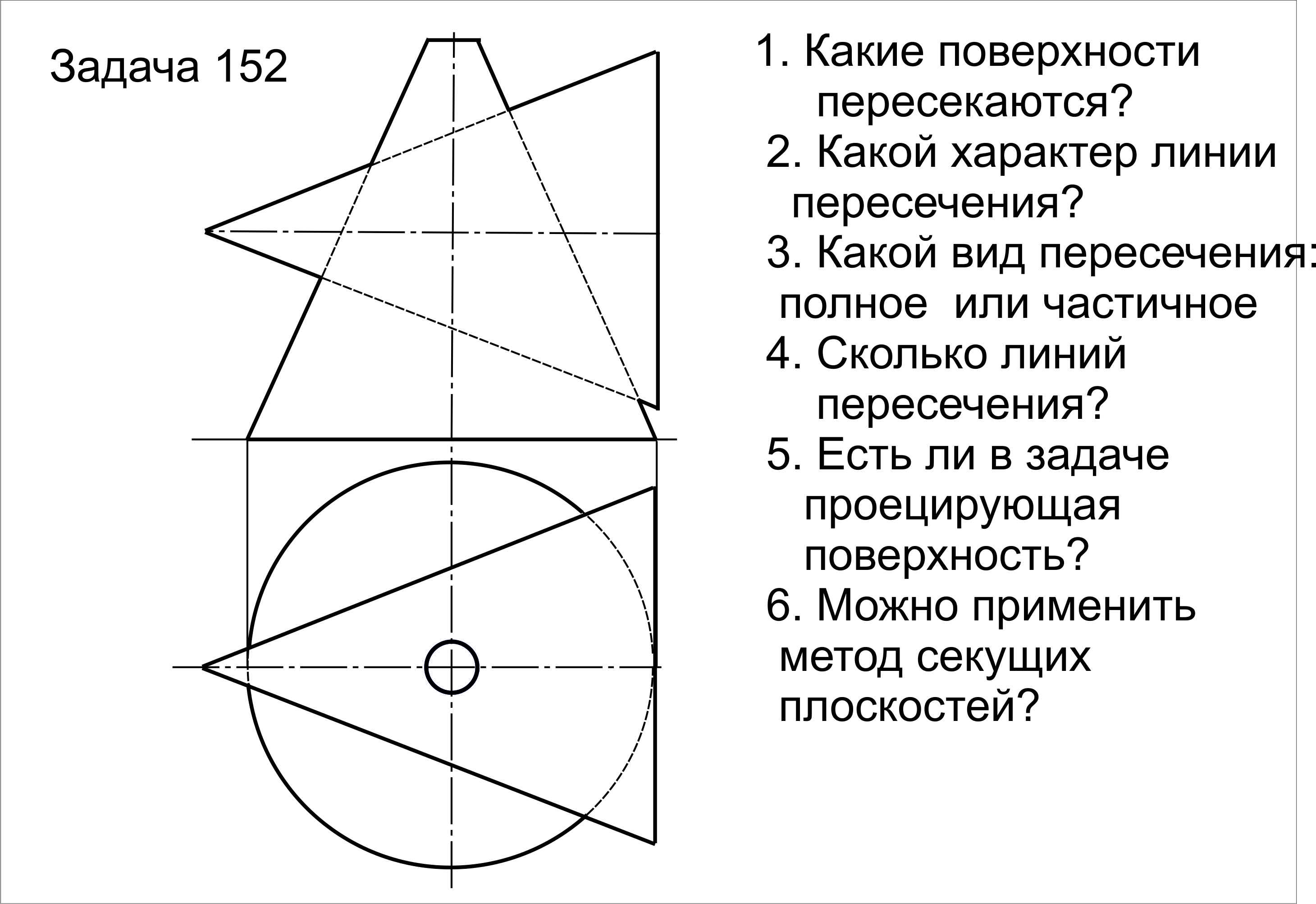
В данном случае обе пересекающиеся поверхности – это поверхности вращения. Оси вращения этих поверхностей пересекаются и образуют плоскость, параллельную фронтальной плоскости проекций П2. Для решения задачи целесообразно применить способ концентрических сфер.
Тема:
Пересечение поверхностей
Для
построения линии пересечения поверхностей,
изображенных на рисунке, применяют
способ …

|
|
|
концентрических сфер |
|
|
|
вспомогательных секущих плоскостей |
|
|
|
замены плоскостей проекций |
|
|
|
эксцентрических сфер |
Решение: В данном случае обе пересекающиеся поверхности – это поверхности вращения. Оси вращения этих поверхностей пересекаются и образуют плоскость, параллельную фронтальной плоскости проекций П2. Для решения задачи целесообразно применить способ концентрических сфер.
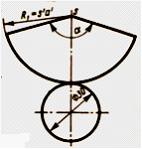
Минимальный
радиус вспомогательной секущей сферы
определяется отрезком …
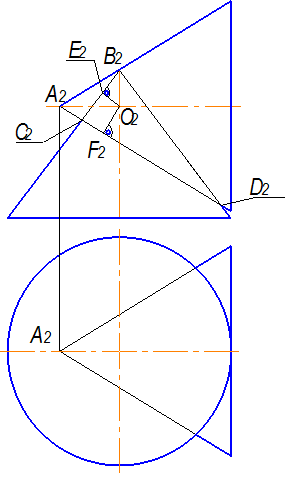
|
|
|
О 2 F 2 |
|
|
|
О 2 A 2 |
|
|
|
О 2 B 2 |
|
|
|
О 2 E 2 |
Решение: Сфера, вписанная в одну из пересекающихся поверхностей и пересекающая другую, будет иметь радиус, определяемый отрезком О 2 F 2. Этот отрезок определит минимальный радиус вспомогательной секущей сферы.
Максимальный радиус вспомогательной секущей сферы определяется расстоянием …
|
|
|
О 2 D 2 |
|
|
|
О 2 C 2 |
|
|
|
О 2 B 2 |
|
|
|
О 2 A 2 |
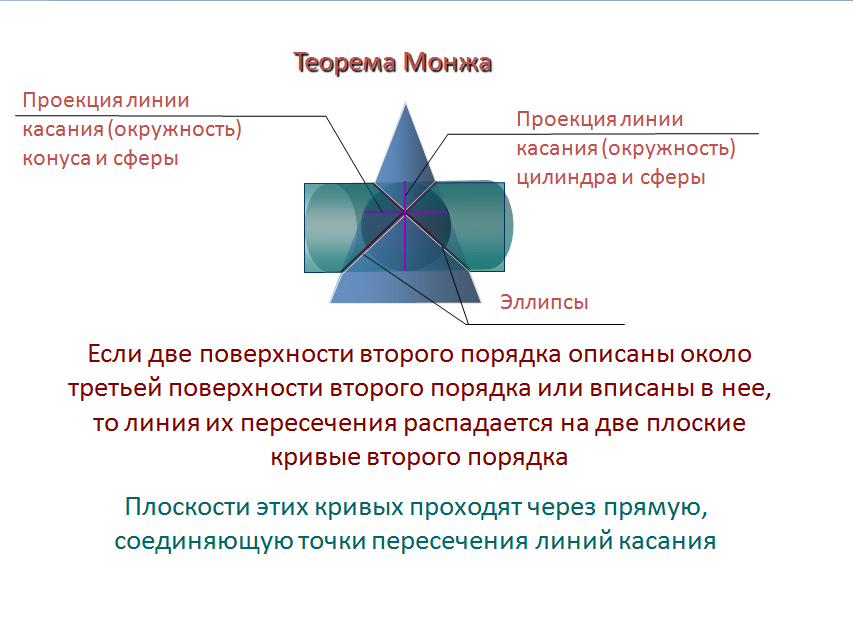
Линии
пересечения конуса и цилиндра, описанных
вокруг одной сферы, на фронтальной
плоскости проекций изображаются в
виде …
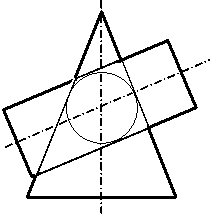
|
|
|
прямолинейных отрезков |
|
|
|
эллипсов |
|
|
|
окружностей |
|
|
|
прямой и окружности |
Заданные
на чертеже поверхности цилиндров
пересекаются по …
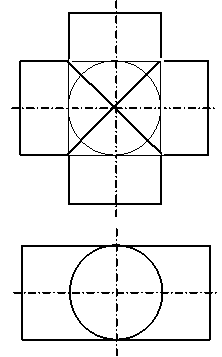
|
|
|
двум эллипсам |
|
|
|
двум прямым |
|
|
|
прямой и окружности |
|
|
|
двум окружностям |
Тема:
Развертки поверхностей
Угол
при вершине кругового сектора развертки
боковой поверхности прямого кругового
конуса равен …
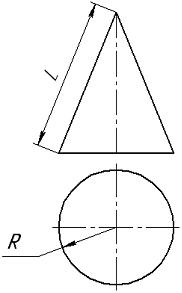
|
|
|
360º |
|
|
|
360º |
|
|
|
180º |
|
|
|
180º |
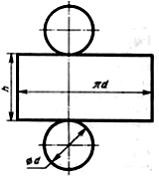
Длина
одной из сторон прямоугольника,
показанного на рисунке, являющегося
разверткой боковой поверхности прямого
кругового цилиндра, равна …
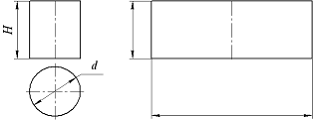
|
|
|
πd |
|
|
|
2πd |
|
|
|
πR |
|
|
|
2πH |
Решение: Развертка поверхности прямого цилиндра представляет собой плоскую фигуру, составленную из боковой поверхности – прямоугольника и двух равных между собой кругов – оснований. Боковая поверхность цилиндра представляют собой прямоугольник, ширина которого равна длине окружности основания – πd, а высота равна высоте цилиндра H.
Развертка ???????? показана на рисунке …
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
Решение: Для построения развертки многогранной поверхности нужно совместить все грани этой поверхности с одной плоскостью так, чтобы образовалась плоская фигура. При этом смежными будут две грани, имеющие общее ребро. Для одной и той же поверхности вид ее развертки может быть различным в зависимости от избранной последовательности расположения граней на развертке. Все грани на развертке изображаются в натуральную величину, поэтому ее построение в общем случае сводится к нахождению натуральных величин отдельных граней поверхности.
Существуют
три способа построения разверток
многогранных поверхностей:
1) способ
нормального сечения;
2) способ
раскатки;
3) способ треугольников
(триангуляции).
Первые два способа
применяются при построении разверток
призматических
поверхностей, третий
– для пирамидальных поверхностей.
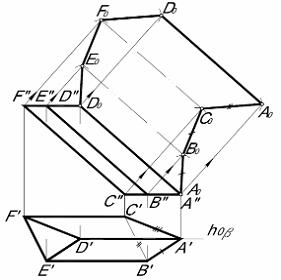
Способ, при котором при построении развертки поверхности призмы строится сечение плоскостью, перпендикулярной к ее боковым ребрам, называется способом …
|
|
|
нормального сечения |
Способ нормального сечения применяют для построения развертки призматических поверхностей. Нормальное сечение проводят перпендикулярно боковым ребрам призмы. На развертке отрезки, равные сторонам нормального сечения, откладываются на прямой линии. Тогда боковые ребра на развертке перпендикулярны этой прямой линии.
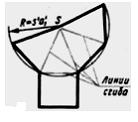
Способ
построения развертки боковой поверхности
наклонного цилиндра, показанный на
рисунке, называется способом …
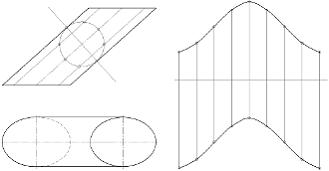
|
|
|
нормального сечения |
|
|
|
раскатки |
|
|
|
треугольников |
|
|
|
прямоугольников |
Решение: Способ, при котором при построении развертки поверхности наклонного цилиндра строится сечение плоскостью, перпендикулярной к его образующим, называется способом нормального сечения. Нормальным сечением наклонного цилиндра, представленного на чертеже, является окружность. Разделив эту окружность на равные части, например, на восемь, через точки делений проводят образующие цилиндра, которые проецируются на плоскость π2 в натуральную величину. Проводится горизонтальная прямая, равная длине окружности нормального сечения, и делится соответственно на восемь равных частей. Через точки делений проводят перпендикуляры, на которых вверх и вниз откладываются длины соответствующих отрезков образующих цилиндра. Концы построенных образующих соединяются плавной линией.
Способ построения развертки призмы, при котором производится последовательное совмещение боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы, называется способом …
|
|
|
раскатки |
|
|
|
нормального сечения |
|
|
|
треугольников |
|
|
|
прямоугольников |
Решение: Способ построения развертки призмы, при котором производится последовательное совмещение боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы, называется способом раскатки. Способ раскатки применяется в том случае, когда основания призмы параллельны одной плоскости проекций, а ее боковые ребра параллельны другой плоскости проекций. Он заключается в последовательном совмещении боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы.
Построение развертки путем разбивки поверхности на треугольники называется методом …
|
|
|
триангуляции |
|
|
|
аппроксимации |
|
|
|
нормального сечения |
|
|
|
раскатки |


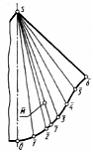
 На
рисунке показана развертка …
На
рисунке показана развертка …