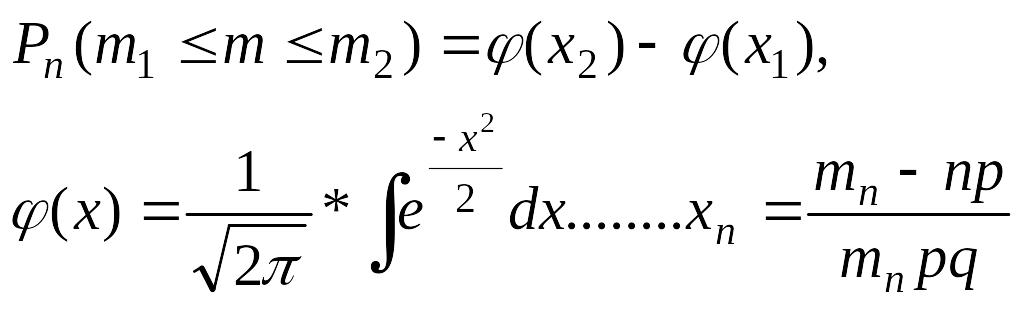- •2 Типы линейных дифференциальных уравнений в частных производных второго порядка
- •Для любой функции алгебры логики существует своя сднф, причем единственная.
- •[Править] Пример нахождения скнф
- •Приведем примеры замкнутых классов.
- •Способы задания графа
- •Минимальное остовное дерево
- •] Пример
- •Классическое определение вероятности
- •Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Бейса
- •Дискретная и непрерывная случайная величина.
- •Числовые характеристики случайной величины.
- •Математическое ожидание. Свойства.
Формула полной вероятности. Формула Бейса
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.
Формулировка
Пусть дано
вероятностное
пространство
,
и полная группа попарно несовместных
событий
![]() ,
таких что
,
таких что
![]()
![]()
![]()
![]() .
Пусть
.
Пусть
![]() —
интересующее нас событие. Тогда
—
интересующее нас событие. Тогда

Замечание Формула полной вероятности также имеет следующую интерпретацию. Пусть N — случайная величина, имеющая распределение
![]() .
Тогда
.
Тогда
![]() ,
т.е. априорная вероятность события
равна среднему
его апостериорной вероятности.
,
т.е. априорная вероятность события
равна среднему
его апостериорной вероятности.
Формула Бейса
Пусть имеется полная группа попарнонесовместных гипотез Н1,Н2…Нn с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло

Последовательности испытаний. Формула Бернулли.
Локальная и интегральная теоремы Лапласа.
Последовательности испытаний
Пусть проводится
конечное число
![]() последовательных
испытаний, в каждом из которых некоторое
событие
последовательных
испытаний, в каждом из которых некоторое
событие
![]() может
либо наступить (такую ситуацию назовём
успехом)
либо не наступить (такую ситуацию
назовём неудачей),
причём эти испытания удовлетворяют
следующим условиям:
может
либо наступить (такую ситуацию назовём
успехом)
либо не наступить (такую ситуацию
назовём неудачей),
причём эти испытания удовлетворяют
следующим условиям:
· каждое испытание случайно относительно события , т. е. до проведения испытания нельзя сказать, появится или нет;
·
испытания
проводятся в одинаковых, с вероятностной
точки зрения, условиях,
т. е. вероятность успеха в каждом
отдельно взятом испытании равна
![]() и
не меняется от испытания к испытанию;
и
не меняется от испытания к испытанию;
·
испытания
независимы,
т. е. события
![]() ,
где
,
где
![]() состоит
в успехе на
состоит
в успехе на
![]() -м
испытании (
-м
испытании (![]() ),
независимы в совокупности.
),
независимы в совокупности.
Такая последовательность испытаний называются схемой Бернулли или биномиальной схемой, а сами испытания - испытаниями Бернулли.
Формула
Бернули
![]()
формула Бернули применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики.
26
Если число испытаний
n
стремится к 0, а вероятность появления
события А в каждом из опытов р стремится
к 0, то для определения вероятности
появления события А ровно m
раз применяют
формулу Пуассона
 a=n*p
a=n*p
Если число опытов достаточно велико но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную теоремы Лапласа
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р, причем 1>р>0, то событие А наступит не менее m1 раз и не более m2 раза приблизительно равно