
- •2 Типы линейных дифференциальных уравнений в частных производных второго порядка
- •Для любой функции алгебры логики существует своя сднф, причем единственная.
- •[Править] Пример нахождения скнф
- •Приведем примеры замкнутых классов.
- •Способы задания графа
- •Минимальное остовное дерево
- •] Пример
- •Классическое определение вероятности
- •Теорема умножения вероятностей.
- •Формула полной вероятности. Формула Бейса
- •Дискретная и непрерывная случайная величина.
- •Числовые характеристики случайной величины.
- •Математическое ожидание. Свойства.
2 Типы линейных дифференциальных уравнений в частных производных второго порядка
Линейные уравнения второго порядка в частных производных подразделяют на параболические, эллиптические и гиперболические.
Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид:

где
A,
B,
C
— коэффициенты, зависящие от переменных
x
и y,
а многоточие означает члены, зависящие
от x,
y,
u
и частных производных первого порядка:
![]() и
и
![]() .
Это уравнение похоже на уравнение
конического сечения:
.
Это уравнение похоже на уравнение
конического сечения:
![]()
Так же, как конические сечения разделяются на эллипсы, параболы и гиперболы, в зависимости от знака дискриминанта D = B2 − AC, классифицируются уравнения второго порядка в заданной точке:
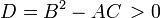 —
Гиперболическое
уравнение,
—
Гиперболическое
уравнение, —
Эллиптическое
уравнение,
—
Эллиптическое
уравнение, —
Параболическое
уравнение
—
Параболическое
уравнение
(здесь предполагается, что в данной точке коэффициенты A, B, C не обращаются в нуль одновременно).
В случае, когда все коэффициенты A, B, C — постоянные, уравнение имеет один и тот же тип во всех точках плоскости переменных x и y. В случае, если коэффициенты A, B, C непрерывно зависят от x и y, множество точек, в которых данное уравнение относится к гиперболическому (эллиптическому), типу образует на плоскости открытую область, называемую гиперболической (эллиптической), а множество точек, в которых уравнение относится к параболическому типу, замкнуто. Уравнение называется смешанным (смешанного типа), если в некоторых точках плоскости оно гиперболическое, а в некоторых — эллиптическое. В этом случае параболические точки, как правило, образуют линию, называемую линией смены типа или линией вырождения.
В общем случае, когда уравнение второго порядка зависит от многих независимых переменных:

оно
также может быть расклассифицирована[1]
(в заданной точке
![]() ),
по аналогии с соответствующей квадратичной
формой:
),
по аналогии с соответствующей квадратичной
формой:
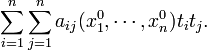
1
Невырожденным линейным преобразованием

квадратичная форма всегда может быть приведена к каноническому виду:
![]()
При этом согласно теореме инерции число положительных, отрицательных и равных нулю коэффициентов λi в каноническом виде квадратичной формы является инвариантом и не зависит от линейного преобразования. На основе этого и производится классификация (в точке M0) рассматриваемого уравнения:
Если в точке M0 квадратичная форма в каноническом виде имеет все коэффициенты одного знака, то уравнение в этой точке называется уравнением эллиптического типа.
Если точке M0 квадратичная форма в каноническом виде имеет коэффициенты различных знаков, но при этом все они отличны от 0, то уравнение в этой точке называется уравнением гиперболического типа.
Если точке M0 квадратичная форма в каноническом виде имеет хотя бы один коэффициент равный 0, то уравнение в этой точке называется уравнением параболического типа.
В случае многих независимых переменных может быть проведена и более подробная классификация (необходимость которой в случае двух независимых переменных не возникает):
Гиперболический тип может быть расклассифицирован на:
Нормальный гиперболический тип, если один коэффициент одного знака, а остальные другого.
Ультрагиперболический тип, если коэффициентов как одного знака так и другого более чем один.
Параболический тип может быть расклассифицирован на:
Эллиптически-параболический тип, если только один коэффициент равен нулю, а остальные имеют один знак.
Гиперболически-параболический тип, если только один коэффициент равен нулю, а остальные имеют различные знаки. Аналогично гиперболическому типу он разделён на:
Нормальный гиперболически-параболический тип
Ультрагиперболически-параболический тип
Ультрапараболический тип, если более чем один коэффициент равен нулю.
2
3 Приведение к каноническому виду дифференциального уравнения второго порядка от двух независимых переменных. Понятие характеристики






 3
3







 4
4





 5
5




 6
6

![]()


 7
7


 8
8



 9
9
Элементарные функции алгебры логики
В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функции, какие приводятся, например, в справочниках). Подобными же способами могут задаваться логические функции.
При использовании табличного способа задания логических функций строится так называемая таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие им значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов (в отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов).
Таблица истинности функций двух аргументов представлена в табл. 1. Существует всего четыре функции одного аргумента.
ТАБЛИЦА 1:

Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n, а число различных функций п аргументов-22n. Так, при n=2 число наборов значений аргументов равно 22=4, число функций 24=16. Таблица истинности логических функций двух аргументов представлена в табл. 2.

Возможен и аналитический способ записи логической функции. В обычной математике аналитический способ представления функции предполагает запись функции в виде математического выражения, в котором аргументы функции связываются определенными математическими операциями. Подобно этому аналитический способ задания логической функции предусматривает запись функции в форме логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.
Функции одного агрумента (табл. 1) представляются следующими выражениями:
f1(x) = 0 (константа 0); f2(x)=x;
f3(х) = х; f4(х) = 1 (константа 1). 10
Устройства, реализующие функции f1(x), f2(x) и f4(x), оказываются тривиальными. Таким образом, из всех функций одного аргумента практический интерес может представлять лишь функция f3(х), которую называют инверсией или логическое НЕ.
Из таблиц истинности функций f0 - f15 (табл. 2) наиболее широко используемыми являются:
f1(x1,x2) = x1*x1 - конъюнкции, логическое произведение, И;
f7(x1,x2) = x1 + x2 - дизъюнкции, логическое сложение, ИЛИ;
f14(x1,x2) = x1 + x2 - логическое И-НЕ;
f14(x1,x2) = x1 * x2 - логическое ИЛИ-НЕ.
Остальные из приведенных в табл. 2 функций либо, либо используются редко.
В дальнейшем функции одного и двух аргументов будем называть элементарными логическими функциями, имея в виду, что логические выражения этих функций, содержащие не более одной логической операции, элементарны.
Свойства конъюнкции, дизъюнкции и инверсии.
Конъюнкция переменных х1 и х2 равна лог. 1 в том случае, когда и x1 и x2 равны лог. 1 (отсюда возникло название операции логическое И).
Дизъюнкция переменных х1 и x2 равна лог. 1, если или х1 или x2 равны лог. 1 (отсюда понятно возникновение названия операции логическое ИЛИ).
В тех случаях, когда число переменных больше двух, конъюнкция их равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из них равна лог. 1.
В математике установлен определенный порядок выполнения операций в сложном выражении. вначале выполняется операция умножения и затем операция сложения. Если требуется изменить порядок, используют скобки.
Операции конъюнкции и дизъюнкции обладают рядом свойств:
сочетательный закон :
x1*(x2*x3) = (x1*x2)*x3 x1+(x2+x3) = (x1+x2)+x3;
переместительный закон:
x1*x2 = x2*x1 x1+x2 = x2+x1;
распределительный закон:
x1+(x2*x3) = (x1+x2) * (x1+x3).
Кроме того, существуют так называемые формулы де Моргана:
x1+x2 = x1 * x2 и x1*x2 = x1 + x2
 11
11
СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.
