[Править] Пример нахождения скнф

Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи Минимизация логических функций методом Квайна:

	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	1	1	1	0	0	0	1	0	0	0	0	0	0	0	1	1

В ячейках строки́ отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.

Четвертый столбец содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:

• = 0 = 0 = 1 = 1

В дизъюнкцию записывается переменная без инверсии если она в наборе равна 0 и с инверсией если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так:

Остальные члены СКНФ составляются по аналогии.

13

Полином Жегалкина — полином(многочлен) над Z₂, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики.

Полином Жегалкина представляет собой сумму по модулю два (операция Исключающее ИЛИ) произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде

или в более формалиизованном виде как

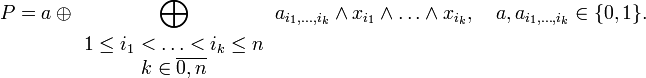
Примеры полиномов Жегалкина:

По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных штук. При этом конъюнкций вида существует ровно 2ⁿ, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.

Полнота и замкнутость системы.

 Определение полноты системы функций в k- значной логике аналогично соот-

ветствующему определению в двузначной логике.

 Определение. Система функций f , …, f из  P называется (функционально)

полной, если любая функция из P может быть записана в виде формулы через функ-ции этой системы.

Для обоснования полноты системы функций в  k – значной логике можно так же

использовать принцип сведения задачи о полноте других систем, 14

Приведем некоторые примеры полных систем в  k – значной логике.

1.      Множество всех функций из  P   является полной системой.

2.Система Россера-Туркетта: {0, 1, …, k-1, J (x),…, J (x), min(x,y), max(x,y)} – полная система в  P . Действительно, для произвольной функции из  P   справедливо равенство, правая часть которого состоит из функций данной системы, т.е. любая функция из  P выражается через эти функции

3.      Система Поста: { , max ( x,y ) } является полной.

4.      Система:  { V (x,y) } – полная. Вопрос о ее полноте может быть легко све-

ден к полноте системы  3. 

            В k – значных логиках исследование произвольной системы функций на полноту сопряжено с большими техническими трудностями: использование критерия полноты, основанного на рассмотрении всех предполных классов в P , даже при k = 3 и 4 требует проверки весьма значительного числа условий т.к. в P существует ровно 18, а в  P – ровно 82  предполных классов.

Доказательство полноты конкретных систем в P проводится обычно методом сведения к заведомо полным системам. С понятием полноты связано понятие замыкания и замкнутого класса, определения которых аналогичны соответственным определениям для двузначной логики.