Способы задания графа
1 Явное задание графа как алгебраической системы.
<{ a,b,c,d },{ u,v,w,x } ; {( u,a ),( u,b ),( v,b ),( v,c ),( w,c ),( w,a ),( x,c ), ( x,d )}>. Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин
2 Геометрический способ
3 Задание графов матрицей смежности:
Матрица смежности – это квадратная матрица порядка p (количество вершин), элемент которой, стоящий в i строке и j столбце определяется по правилу:
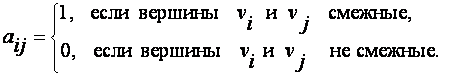
ПРИМЕР
2. Задание графов матрицей инцидентций.
Матрицей
инцидентции
называется прямоугольная матрица
размерности
(p
–
количество
вершин, q
– количество ребер), элемент которой
стоящий в i
строке и j
столбце определяется по правилу:
- для неориентированного графа.
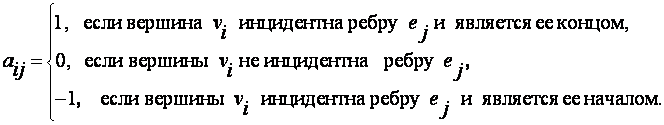
- для ориентированного графа.
Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.
П
ример
1 (изоморфизм). Покажем,
что следующие два графа изоморфны.
Действительно, отображение a
® e,
b ® f,
c ® g,
d ® h
, являющееся
изоморфизмом легко представить как
модификацию первого графа, передвигающую
вершину d в
центр рисунка.
17
Дерево решен. Остовное дерево. Жадный алгоритм. Алгоритм ближайшего соседа.
Возможности выбора при решении проблемы можно представить в виде ориентированного дерева, где в корне – проблема, дуге соответствует один из вариантов выбора, вершине - новая ситуация, возникающая в результате реализации приписанного дуге варианта. Такой трактовке соответствует граф типа дерева, получивший название «дерево решений». Предположим, что можно оценить эффективность принятого выбора. Тогда возникает задача поиска среди возможных путей от корня (когда проблема поставлена) к одному из листьев (когда проблема решена) пути, имеющего оптимальную оценку.
Минимальное остовное дерево
Если ребра графа взвешены, то возникает задача выделения остова с минимальной или максимальной оценкой. Предположим, что вершинам графа сопоставлены полюса схемы, на которые необходимо подать питание, а ребрам - разрешенные связи для цепи питания. Тогда любой из остовов будет определять вариант цепи питания. Действительно, цепи сопоставляется граф без петель, включающий все вершины. Если веса определяют расстояние между полюсами, то остову с минимальной суммой весов соответствует разводка питания с минимальной суммарной длиной проводников. Такая задача решается при трассировке печатных плат. Может быть предложена такая трактовка задачи. Вершины - абоненты, связанные линиями связи, веса на ребрах - оценка потери конфиденциальной информации при ее передаче по этой линии связи. Тогда задаче выделения остова с минимальным произведением весов, входящих в остов ребер, соответствует задача определения наиболее надежной сети для передачи информации.
Жадный алгоритм Выбирается ребро, имеющее минимальный вес среди всех рёбер, и включается в остов. Из оставшихся ребер выбирается снова то, которое имеет минимальный вес, и включается в остов, если при этом не образуются циклы. Процесс продолжается до тех пор, пока все вершины не будут включены в остов. Алгоритм прост для понимания и обеспечивает получение минимального решения. Однако сложность его состоит в том, что в нем неявно присутствует процедура проверки на появления циклов, которая связана с перебором по всему графу, так же как и поиск очередного ребра.
Алгоритм ближайшего соседа — один из простейших эвристических методов решения задачи коммивояжёра. Относится к категории «жадных» алгоритмов.
Формулируется следующим образом: Пункты обхода плана последовательно включаются в маршрут, причем, каждый очередной включаемый пункт должен быть ближайшим к последнему выбранному пункту среди всех остальных, ещё не включенных в состав маршрута. Алгоритм прост в реализации, быстро выполняется, но, как и другие «жадные» алгоритмы, может выдавать неоптимальные решения. Одним из эвристических критериев оценки решения является правило: если путь, пройденный на последних шагах алгоритма, сравним с путём, пройденным на начальных шагах, то можно условно считать найденный маршрут приемлемым, иначе, вероятно, существуют более оптимальные решения. Другой вариант оценки решения заключается в использовании алгоритма нижней граничной оценки Для любого количества можно подобрать такое расположение, что алгоритм ближайшего соседа будет выдавать наихудшее решение 18
Кратчайшие пути на графе. Алгоритм Дейкстры.
Алгори́тм Де́йкстры (Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.