П .15.3. Определение собственный значений и собственных функций методом Келлога.
Собственные функции и собственные значения ядра могут быть найдены методом последовательных приближений,который называется методом Келлога,т.е будем медленно приближаться к решению.
Рассмотрим
след.уравнение: y(x)=
=
y(s)ds
(5)
В
случае,когда ядро
удовлетворяет условиям (4):
1)возьмем
произвольную непрерывную функцию
такую что А
определим рекуррентно
=
А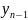
и получим
.
Обозначим
имеет место соотношение
(6)потом будет выполняться p+q=2n.Пусть
p+n+m,
q=n-m
,тогда в силу симметрии А имеем
=(
Для
нормированных функций
=
из (6) получаем
;
.
Из (6)получаем (7).
2)можно
доказать,что существует предел
3)убедимся
в том ,что
,значит
действительно
выбрано так,что
А
. При этом
>0
из неравенства Коши-Буняковского следует
≤
,
значит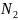
,
аналогично
,
,n≥0
n
4)можно
доказать,что четные итерации
сходятся в среднем к некоторой функции
(х),а
нечетные итерации
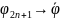(х)
;
(х)
равномерно сходится,
(х)
Совершая
предельный переход по четным и нечетным
номерам в (7) будем иметь
=
,
=
(8) отсюда получится равенство
=
(
последнее равенство возможно в двух
случаях:
А)
,
=
в этом случае
собственным значением уравнения (5) ,а
из (8)следует
Б)z
=
(
или z= -
-
является собственным значением уравнения
(5) из (8) следует тогда ,что z=
=
.
Значит λ=
,
y=
;
λ=
,
y=
следовательно является собственной
функцией и собственным значением
уравнения (5).
Пример
1. y(x)=
(9)
,
=
-
=
-
*
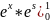Находим лимит:
Строим
нормированные функции:
=
Таким
образом
является собственной функцией
интегрального уравнения 9 соответствующ.
собствен.значению λ= -
П. 15.4 Вырожденные ядра
Опр-е:
ядро К(х,s) представленное
конечной суммой вида К(х,s)=
(10) называется вырожденным ядром
Теорема 15:1)вырожденное ядро имеет конечное число собственных значений 2)если симметричное ядро К(x,s) имеет конечное число собственных значений,то оно вырождено .
Покажем технику таких уравнений на примерах.
Пример2.
Определим собст. значения и собст.
функции интегрального уравнения y(x)=
(11)
К(х,s)=x-s=x*1-1*s
– несимметрическое вырожденное ядро,оно
явл-ся многочленном 1 степени отн-но
х,поэтому решение имеет вид
y(x)=ax+b,подставляя
это выражение в 11: ax+b=
+xb-a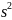
-bs)ds=λ(
+xbs-
Приравниваем
коэффициенты при х:
- система однородных алгебраических
уравнений
Имеет нетривиальное решение,когда ее определитель =0
∆=
4
;
A=
=
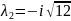
кансенсунс
Лекция 16. Неоднородные уравнения Фредгольма 2 рода
П.16.1.в случае симметричного ядра
Рассмотрим
неоднородное уравнение Фредгольма 2
рода y(x)=
в котором f(x)
является вещественной непрерывной на
отрезке
функций ядро K(x,s)
удовлетворяет условиям :
K(x,s)-вещественная функция
K(x,s)≢0 (2)
K(x,s)-непрерывная по совокупности аргументов
Симметричное ядро: K(x,s)= K(s,x)
Теорема
16.1.пусть ядро K(x,s)удовлетворяет
требованиям (2),тогда λ не совпадает
не с одним собственным значением ядра
K(x,s),то
решение ИУ существует единственно и
представимо в виде: y(x)=f(x)+
(3)
y(x)=f(x)+
(4)
R
=
+
(5)
–резольвента ядра
Если
,где
-некоторое
собственное значение ядра
и функция f(x)
ортогональна всем собственным функциям
соответств.
,то
решения уравнения (1) существует и не
является единственным y(x)=f(x)+
+
(6),
где
=const;
=(f,
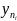)=0
i=1…p
Если же
и f(x)
ортогональна
хотя бы одной собственной функции f(x)
не ортогональна
(x),то
решение не существует
Пример
1. y(x)=λ
y(x)=λ
=A
(8) ,где A и B
–некоторые коэффициенты
подставляя
(8) в (7) имеем : A
=λ
=
+
=
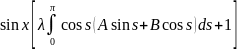B+1)
+
A-1)
получим
систему,приравнивая коэффициенты при
и
(9)
однородному
уравнению (7) соответствует однородная
система (9),т.е система полученная (9)
заменой свободных членов нулями,ее
определитель:
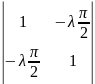=0
найдем λ:
соответствующие
решения однородной системы (9) A=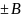
cобственные функции
однородного уравнения (7):
множитель
выбран из условия нормировки
1 случай
при
из (9) A=
,
B=-A
Y(x)=
– решение будет таким
Этим проиллюстрировано первое утверждение теоремы 16.1 при решение уравнения (7) существует и единственно.
2 случай
при
из (9)получается при подстановки
Y(x)=A
,где
А-произвольная константа ,решение
уравнения (7)существует ,но не единственно
Собств.
значению
ядра
=
соответствует собственная функция
(x)=
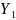(x)dx=
dx=0
. этим проиллюстрировано второе
утверждение теоремы 16.1
,тогда
система (9) не совместна ,решения у ИУ
(7) нет .Совместному значению
соответствует собственная функция
(x)=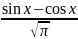
.В этом случае не выполнено необходимое
условие существования решения уравнения
(7),т.к
(x)dx=
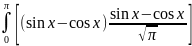dx=2
=0
следовательно решений нет.Этим
проиллюстрировано 3 утверждение теоремы
16.1.
П.16.2. Случай малого λ.
Пусть
и f(x)
произвольно-непрерывные при x,s
.
Симметрия
от
не требуется ,обозначим sup
=
(a≤x≤b,
a≤s≤b)
Теорема
16.2:если
,то
решение уравнения (1) существует и
единственно ,решение может быть найдено
как предел равномерно-сходящейся
последовательности приближений
(x)
определяемых рекуррентным соотношением
+f(x)
(10) ,где
-произвольная
непрерывная функция.
Лекция 17. Уравнение Вольтера 2 порядка.
П.17.1.Существование и единственность решений.
Рассмотрим
интегральное уравнение Вольтера 2 рода:
y(x)=λ
,
где
-непрерывные
функции a
Теорема 17.1: уравнение (1) имеет единственное непрерывное решение при любом λ это решение может быть найдено путем последовательных приближений.
Замечания1:однородное уравнение (1) имеет лишь тривиальное решение ,значит однородное уравнение Вольтера 2 рода не имеет собственное значений.
Замечание2:поскольку собственных значений не существует ,то множитель λ в записи урачвнения Вольтера обычно опускают.
Пример1.
Y(x)=
1
способ. Продифференцируем уравнение
(2) дважды:
(x)=
Решаем полученное дифференциальное уравнение с учетом y(0)=0, (0)=0
;
=0,
=0
2
способ. Найдем решение путем последовательных
приближений,выбираем
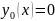
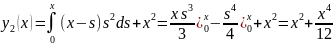
Y(x)=
.
Уравнение
(3) может быть сведено к интегральному
уравнению 2 рода.
и f(x)
дифференцируемы по x
x
тогда дифференцируя соотношения (3)
имеем
деля на
приходим
к уравнению Вольтера 2 рода:
y(x)=
,
g(x)=
П.17.2. резольвента для уравнения Вольтера.
Обозначим оператор Вольтера через В:
By:
Определим
повторное ядро Вольтера так:
y=
(4),тогда
y=
=
=
M=sup при a
Тогда
справедлива оценка :
(5), используя (4) имеем
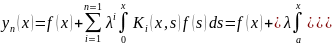
R(x,s,λ)=
Переходя
в (6) к пределу под знаком интеграла
получим:y(x)=f(x)+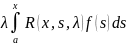
.
Это соотношение представляет собой
выражение решение уравнения (1) через
резольвенту R(x,s,λ)
Теорема 17.2:решение уравнения (1) представлено в виде (7), где резольвента R(x,s,λ),определяемая рядом (6а) является непрерывной функцией при a любое λ
Пример2. Построим резольвенту для уравнения (2)
Y(x)=
=
Таким образом при λ=1
Y(x)=
=
=2[ch
x
-1]
Лекция 18. Решение задач о теплопроводности с неоднородными граничными условиями
В лк 10 мы рассмотрели уравнение теплопроводности (10.1) с однородными граничными условиями 10.2 u(0,t)=0, u(1,t)=0. В данной лк мы разберем ,т.о задачу:
(УЧП):
.
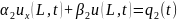
(НУ):
u(x,0)=
ЭТУ ЗАДАЧУ МОЖНО СВЕСТИ К ВИДУ:
u(x,0)=
эта задача может быть решена методом разделения переменных . Рассмотрим в лк 10 метод разделения переменных является достаточно мощным ,а получаемые с его помощью решения подставляются в удобной форме ,однако этот метод применим не для всех задач. Для применимости метода разделения переменных граничные условия должны быть линейно однородными ,т.е представляться в виде:
Цель этой лк показать каким образом задача с неоднородными граничными условиями вида:
(УЧП):
.
(НУ): u(x,0)=
Эта задача может быть решена путем сведения к задаче с однородными граничными условиями . начнем с простого примера преобразования неоднородных граничных условий к однородным.
П.18.1. преобразование неоднородных граничных условий к однородным
Рассмотрим задачу по распространению тепла в теплоизолированном стержне :
(УЧП):
(ГУ):
(2)
(НУ):
u(x,0)=
Мы
не можем ее решать методом разделения
переменных ,однако при t
решение задачи (2) стремится к стационарному
решению ,которое линейно изменяется
вдоль x
от температуры
и
Решение задачи (2) в различные моменты времени :а) начальная температура u(x,0)=
Б)u(x,
стационарная
В)переходная температура
Разумно
предположить ,что температуру в нашей
задаче можно представить в виде суммы
двух слагаемых: u(x,
стационарная + переходная =[
u(x,
Стационарная- предельное решение для больших времен; переходная-часть времени которая зависит от НУ и стремится к нулю с ростом времени
Исходную задачу (2) мы приводим к новой задаче отн-но неизвестной u(x, и добавить ее к стационарному решению .в результате чего получиться искомая функция u(x, ,проделав эти простые преобразования с (2) ,получим:
(УЧП):
(ГУ):
(3)
(НУ):
u(x,0)=
[
=
,
где
.
Это задача не только с однородным
уравнением ,но и с однородными граничными
условиями,что позволяет решать ее
методом разделения переменных
В
лк 10 мы получили решение u(x,
Это все ,что касается стержней с фиксированными температурами на концах. Что же можно сказать о более реалистических граничных условиях ,зависящих от времени правыми частями?
П .18.2. преобразование зависящих от времени граничных условий в нулевые
Рассмотрим типичную задачу уравнения в частных производных :
(УЧП):
(ГУ):
(НУ): u(x,0)=
Для
того,чтобы преобразовать эти граничные
условия в нулевые мы остановились на
следующей форме решения: u(x,
,где
функции
выбираются так чтобы квазистационарная
часть решения (6) : s(x,
удовлетворяла граничным условиям
исходной задачи . в этом случае функция
u(x,
будет удовлетворять однородным граничным
условиям . подстановка функции s(x,
в граничные условия: s(0,
,
Приводят
к двум уравнениям ,из которых можно
определить
в результате получаем
,
(7) след-но u(x,
Если
подставить эти выражения для u(x,
в исходную задачу мы получи новую задачу
для неизвестной функции u(x,
(УЧП):
-
(неоднородное УЧП)
(ГУ):
(однородное ГУ)
(НУ):
u(x,0)=
(новое НУ известной функцией)
Теперь перед нами новая задача с однородными граничными условиями при этом ,к сожалению,уравнение стало неоднородным ,мы не можем решить эту задачу методом разделения переменных однако ее можно решить методом интегральных преобразований и разложением по собственным функциям.
Замечание 1. Цель этой лк была научиться преобразовывать задачи с неоднородными граничными условиями в задачи с нулевыми граничными условиями . после того,как это сделано может случиться ,что новое уравнение с частными производными станет однородным . если это произойдет ,то задачу можно решать методом разделения переменных .если же преобразованное уравнение не стало однородным,то новую задачу нужно решать каким-либо другим методом.
Замечание2. Линейно неоднородные граничные условия наиболее общего вида :
L
нулевым граничным условиям ,если
воспользоваться методом описанном в
(2) ,конечно новое уравнение ,вероятнее
всего ,будет неоднородным .
некоторые
методы решения не содержат никаких
требований однородности граничных
условий значит не требуют никаких
предварительных преобразований
,например, методом преобразования
Лапласа мы убедимся в том ,что нулевые
граничные условия не обязательны. В
случае нулевых граничных условий решение
находиться несколько проще ,чем в других
случаях.
ечание4.
Для граничных
условий вида:
,
Метод изложенный в этом пункте приводит к следующей форме решения задачи :
u(x,
u(x,