П.14.3. Особенности постановки задачи для уравнения Фредгольма.

Предыдущий пример показывает ,что уравнение Фредгольма может содержаться параметр(в том случае был ),которого выбирают так,чтобы решение ,поэтому в общем случае однородное уравнение Фредгольма 2 рода записывается в виде: y(x)=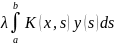 (11), где 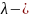неизвестный параметр

Все значения при которых уравнение (11) имеет нетривиальное решение называется собственными значениями уравнения (11) и отвечающее этим значениям нетривиальное решение называется собственными функциями ИУ (11).Неоднородное уравнение Фредгольма 2 рода также записывается параметром : y(x)= +f(x) (12), здесь обычно является заданной величиной ,мы увидим,что совпадает одним из собственных значений ядра K(x,s),то уравнение (12) имеет решение не при любой функции f(x). Для струны это означает,что если частота возмущающая гармоническая сила 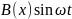совпадает с собственной частотой колебаний струны,то возникает резонанс и не будет гармонических колебаний.

Лекция 15. Однородное уравнение Фредгольма 2 рода.

П.15.1. Некоторые введения из теории операторов в Гильбертовом пространстве.

Пусть H-сепарабельное гильбертовое пространство

Определение:нормой оператора А обозначается норма IIAII называется неотрицательное число,определяемое следующим образом : IIAII=sup ,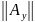

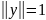
Если существует норма 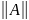, то оператор называется ограниченным, в противном случае оператор называется неограниченным

Теорема 15,2:

Если оператор А непрерывен для любого y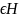 ,то будем говорить,что он не прерывен в H или просто не прерывен ,где H-гильбертово пространство ,т.е бесконечномерное евклидово пространство

Теорема 15.3:ограниченный оператор является непрерывным

Теорема 15.4:непрерывный оператор является ограниченным

Определение:оператор А является вполне не прерывным в H , если любая последовательность векторов 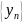он переводит в компактную посл-ть 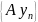. Напомним ,что множество М- компактно ,если из любого покрытия 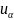его открытыми множествами можно выделить конечное подпокрытие.

Теорема 15.5:вполне непрерывный оператор является ограниченным

Теорема15.6: если ядро K(x,t) непрерывно при a≤x≤b, a≤t≤b, то оператор Фредгольма (1) является вполне непрерывным

Определение:симметричным или самосопряженным оператором называется оператор А,удолетворяющий условию : ( ) любой y

Теорема15.7:оператор Фредгольма является симметричным ,если K(x,t)=K(t,x)

Теорема 15.8: всякий симметричный вполне непрерывный оператор А обладает собственным вектором, которому отвечают собственные значения λ,причем =

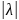Пусть задан вполне симметричный непрерывный оператор А

Теорема15.9:собственные векторы,отвечающие различным собственным значениям оператора А ортогональны между собой .

Теорема 15.10:имеется не более конечного числа линейно-независимых собственных векторов оператора А для которых отвечающие им собственные значения удовлетворяют неравенству >0, .

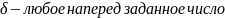П.15.2. Собтвенные функции и собственные значения однородного уравнения Фредгольма 2 рода

Y(x)= ,x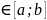 (3)

Определение:значение параметра при котором существуют нетривиальные решения уравнения (3) называется собственным значением уравнения (3) а само нетривиальное решение называется собственной функцией уравнения (3)

Будем предполагать,что ядро K(x,s) x,s ,удовлетворяют следующим условиям:

1)K(x,s)-вещественная функция

2) K(x,s)

3) K(x,s) непрерывная по x и s

4) K(x,s)= K(s,x)

Теорема15.11: 1)собственные значения ядра K(x,s)-вещественные; 2)нахождение комплексных собственных функций сводится к нахождению вещественных собственных функций

Теорема15.12: если K(x,s)-непрерывно и K(x,s)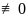 ,то норма оператора Фредгольма отлична от нуля

Определение:рангом собственного значения называется max число ,отвечающих ему лин.-независимых собственных векторов

Теорема15.13: 1)существует конечная и бесконечная посл-ть лин.-независимых собственных функций и соответствующих собственных значений ядра K(x,s) 2) собственные функции соответствующим различным собственным значениям ортогональны.Ранг любого собственного значения конечен.Всю систему собственных функций можно ортонормировать так, чтобы были выполнены соотношения ; 3)какого бы ни было L>0 может существовать лишь конечное число собственных значений ,удовлетворяющих неравенству 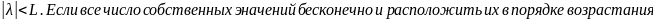абсолютной величиной : = . Допустим мы нашли собственное значение 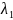и собственную функцию ,тогда можно применить след. теорему:

Теорема15.14:если -собственная функция ядро K(x,s) и -соответствующее собственное значение,то ядро K(x,s)- ,то ядро имеет те же собственные значения и собственные функции,что и ядро K(x,s),кроме и