7 Вычеты. Применение их к вычислению интегралов

7.1 Вычет функции и его вычисление

Пусть функция аналитична в некоторой окрестности точки за исключением, быть может, самой точки .

Определение. Вычетом функции относительно точки (обозначается или ) называется число, равное

, (71)

где – простой замкнутый контур, лежащий в области аналитичности функции и содержащий внутри себя только одну особую точку . В качестве удобно брать окружность достаточно малого радиуса .

Из определения (71) вытекает, что вычет функции совпадает с коэффициентом разложения ее в ряд Лорана по степеням :

. (72)

Из представления (71) следует, что вычет в правильной и устранимой особой точках равен нулю. Вычет в простом полюсе определяется по формуле

. (73)

Если функция в окрестности точки является частным двух аналитических функций

,

причем , , и – простой полюс функции , то

. (74)

Вычет функции в полюсе порядка определяется по формуле

. (75)

Если точка – существенно особая точка функции , то для определения вычета необходимо найти коэффициент , в лорановском разложении функции в окрестности точки .

Пример 1. Найти вычеты функции 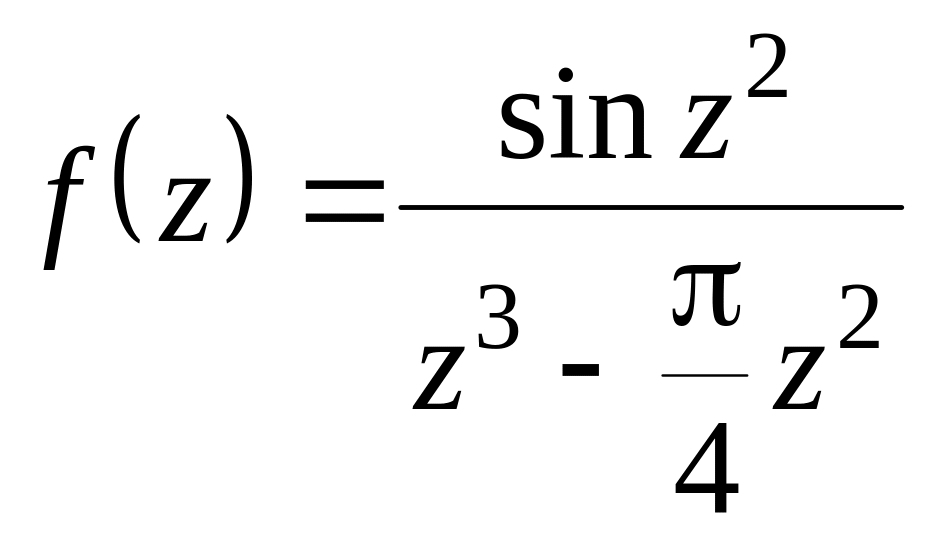в ее особых точках.

Особыми точками являются точки и .

В точке найдем: , т.е. точка – устранимая особая точка функции . Поэтому .

В точке , т.е. точка - полюс (первого порядка) функции. По формуле (73) имеем .

Пример 2. Определить вычет функции относительно точки .

Точка является полюсом третьего порядка функции, т.к. . В соответствии с (75) получим:

.

Пример 3. Найти вычет функции в ее особых точках.

Особой для данной функции является точка . Это – существенно особая точка (из свойств функции следует, что существует ). Для определения вычета найдем коэффициент разложения функции в ряд Лорана по степеням . Так как , следовательно .

7.2 Основная теорема о вычетах и ее применение к вычислению контурных интегралов

Теорема Коши (основная теорема о вычетах). Если функция аналитична на границе области и внутри области, за исключением конечного числа изолированных особых точек , то

(76)

Замечание. Теорему Коши о вычетах удобно использовать, когда внутри контура интегрирования находится небольшое число особых точек.

Пример 1. Вычислить интеграл , где .

Особыми точками подынтегральной функции являются – полюс второго порядка, – полюсы первого порядка. Внутри окружности (рисунок 16) лежит лишь точка . Поэтому по формуле (76)

.

Рисунок 16

Пример 2. Вычислить интеграл .

В области функция имеет две особые точки: – полюс первого порядка и – существенно особую точку.

По формуле (74) . Для нахождения вычета в точке необходимо иметь лорановское разложение функции в окрестности точки . Из представления функции в виде следует, что в ее лорановском разложении содержатся только четные степени и , так что и . По теореме Коши о вычетах (76) .