
Задача RMQ — 1. Static RMQ
RMQ
расшифровывается как Range Minimum (Maximum) Query
– запрос минимума (максимума) на отрезке
в массиве. Для определённости мы будем
рассматривать операцию взятия
минимума.
Пусть
дан массив A[1..n]. Нам необходимо уметь
отвечать на запрос вида «найти минимум
на отрезке с i-ого элемента по
j-ый».
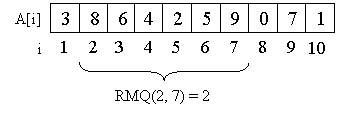 Рассмотрим
в качестве примера массив A = {3, 8, 6, 4, 2,
5, 9, 0, 7, 1}.
Например,
минимум на отрезке со второго элемента
по седьмой равен двум, то есть RMQ(2, 7) =
2.
Рассмотрим
в качестве примера массив A = {3, 8, 6, 4, 2,
5, 9, 0, 7, 1}.
Например,
минимум на отрезке со второго элемента
по седьмой равен двум, то есть RMQ(2, 7) =
2.
Для
оценки эффективности алгоритма введём
ещё одну временнýю характеристику –
время препроцессинга. В ней будем
учитывать время на подготовку, т.е.
предподсчёт некоторой информации,
необходимой для ответа на запросы.
Начиная
с этого момента будем обозначать
временные характеристики алгоритма
как (P(n), Q(n)), где P(n) – время на предподсчёт
и Q(n) – время на ответ на один запрос.
Научимся
решать задачу за (O(nlogn), O(1)), где logn –
двоичный логарифм n.
Sparse Table – это
таблица ST[][] такая, что ST[k][i] есть минимум
на полуинтервале [A[i], A[i+2k]).
Иными словами, она содержит минимумы
на всех отрезках, длина которых есть
степень двойки.
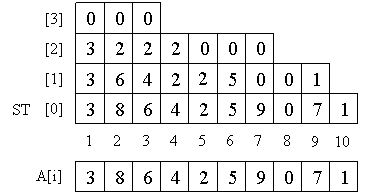 Насчитаем
массив ST[k][i] следующим образом. Понятно,
что ST[0] просто и есть наш массив A. Далее
воспользуемся понятным свойством:
ST[k][i]
= min(ST[k-1][i], ST[k-1][i + 2k
— 1]).
Благодаря нему мы можем сначала посчитать
ST[1], потом ST[2] и т. д.
Заметим, что
в нашей таблице O(nlogn) элементов, потому
что номера уровней должны быть не больше
logn, т. к. при больших значениях k длина
полуинтервала становится больше длины
всего массива и хранить соответствующие
значения бессмысленно. И на каждом
уровне O(n) элементов.
Заметим, что
любой отрезок массива разбивается на
два перекрывающихся подотрезка длиною
в степень двойки.
Насчитаем
массив ST[k][i] следующим образом. Понятно,
что ST[0] просто и есть наш массив A. Далее
воспользуемся понятным свойством:
ST[k][i]
= min(ST[k-1][i], ST[k-1][i + 2k
— 1]).
Благодаря нему мы можем сначала посчитать
ST[1], потом ST[2] и т. д.
Заметим, что
в нашей таблице O(nlogn) элементов, потому
что номера уровней должны быть не больше
logn, т. к. при больших значениях k длина
полуинтервала становится больше длины
всего массива и хранить соответствующие
значения бессмысленно. И на каждом
уровне O(n) элементов.
Заметим, что
любой отрезок массива разбивается на
два перекрывающихся подотрезка длиною
в степень двойки.
 Получаем
простую формулу для вычисления RMQ(i, j).
Если k = log(j – i + 1), то RMQ(i, j) = min(ST(i, k), ST(j –
2k +
1, k)). Тем самым, получаем алгоритм за
(O(nlogn), O(1)). Ура!
Получаем
простую формулу для вычисления RMQ(i, j).
Если k = log(j – i + 1), то RMQ(i, j) = min(ST(i, k), ST(j –
2k +
1, k)). Тем самым, получаем алгоритм за
(O(nlogn), O(1)). Ура!
Задача RMQ – 2. Дерево отрезков
Введём понятие дерева отрезков. Для удобства дополним длину массива до степени двойки. В добавленные элементы массива допишем бесконечности (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится). Итак, дерево отрезков это двоичное дерево, в каждой вершине которого написано значение заданной функции на некотором отрезке. Функция в нашем случае – это минимум. Каждому листу будет соответствовать элемент массива с номером, равным порядковому номеру листа в дереве. А каждой вершине, не являющейся листом, будет соответствовать отрезок из элементов массива соответствующих листам-потомкам этой вершины.
П остроение
Построим
дерево, пробежавшись по элементам с (n
– 1)-ого по первый, считая минимум значений
в сыновьях для каждой вершины.
const
int
INF
= INT_MAX;
остроение
Построим
дерево, пробежавшись по элементам с (n
– 1)-ого по первый, считая минимум значений
в сыновьях для каждой вершины.
const
int
INF
= INT_MAX;
void build_tree(const vector<int>& V)
{
// размер, доведённый до степени двойки
int n = (1 << (log(n - 1) + 1));
V.resize(2 * n, INF);
// инициализируем листы
for (int i = n; i < 2 * n; i++)
V[i] = V[i - n];
// и все остальные вершины
for (int i = n - 1; i > 0; i--)
V[i] = min(V[2 * i], V[2 * i + 1]);
}
Функция build_tree(V) превращает массив V в дерево отрезков для этого массива
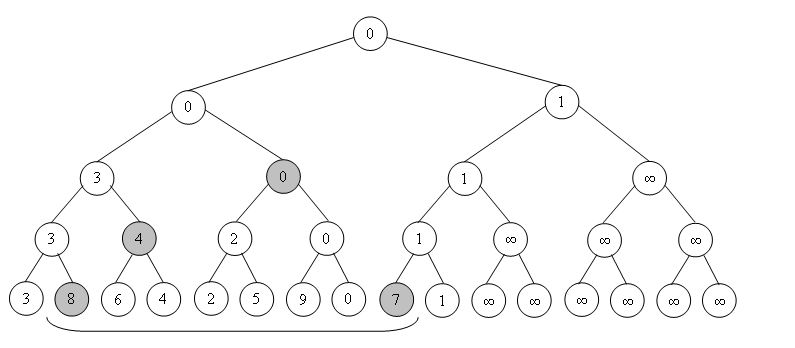 Поясним
определение. Выделенной вершине будет
соответствовать отмеченный отрезок,
потому как он является объединением
всех листов-потомков данной вершины
(начиная с этого момента отождествим
лист и элемент массива, который он
представляет).
Хранить дерево будем
подобно двоичной куче. Заведём массив
T[2n – 1]. Корень будет лежать в первом
элементе массива, а сыновья i-ой вершины
будут лежать в элементах с номерами 2i
и 2i + 1 – левый и правый соответственно.
Сразу можно заметить очевидное свойство:
T[i] = min(T[2i], T[2i + 1]) для i-ой вершины, не
являющейся листом. Листы, к слову, будут
лежать при такой нумерации в элементах
с номерами от n до 2n – 1.
Назовём
фундаментальным отрезком в массиве
такой отрезок, что существует вершина
в дереве, которой он соответствует.
Разобьём наш отрезк на минимальное
количество непересекающихся
фундаментальных. Покажем, что на каждом
уровне их количество не превосходит
2.
Возьмём
самый большой фундаментальный отрезок
в разбиении. Пусть его длина – 2t. Заметим,
что фундаментальных отрезков длиной
2t – не более двух (1). Возьмём самый левый
из имеющихся максимальных фундаментальных.
Будем двигаться от него налево. Заметим,
опять же, что длины отрезков будут
убывать (2). Так же и с правым из максимальных.
Тем самым получим, что фундаментальных
отрезков – не более 2t, что не превосходит
2logn. Пункты (1) и (2) в доказательстве я
оставлю для самостоятельного
осмысления.
Чем нам это помогает?
Теперь мы можем реализовать запрос
минимума «снизу». Будем подниматься
снизу, добавляя к ответу на каждом
уровне, если надо, фундаментальный
отрезок.
Заведём два указателя – l и
r, с помощью которых будем находить
очередные фундаментальные отрезки
разбиения. Изначально установим l и r
указывающими на листы, соответствующие
концам отрезка запроса. Заметим, что
если l указывает на вершину, являющуюся
правым сыном своего родителя, то эта
вершина принадлежит разбиению на
фундаментальные отрезки, в противном
случае не принадлежит. Аналогично с
указателем r – если он указывает на
вершину, являющуюся левым сыном своего
родителя, то добавляем её в разбиение.
После этого сдвигаем оба указателя на
уровень выше и повторяем операцию.
Продолжаем операции пока указатели не
зайдут один за другой.
Находя очередной
фундаментальный отрезок, мы сравниваем
минимум на нём с текущим найденным
минимумом и уменьшаем его в случае
необходимости. Асимптотика работы
алгоритма – O(logn), т. к. на каждом уровне
мы выполняем константное число операций,
а всего уровней – logn.
int
rmq_up(vector<int>&
T,
int
l,
int
r)
Поясним
определение. Выделенной вершине будет
соответствовать отмеченный отрезок,
потому как он является объединением
всех листов-потомков данной вершины
(начиная с этого момента отождествим
лист и элемент массива, который он
представляет).
Хранить дерево будем
подобно двоичной куче. Заведём массив
T[2n – 1]. Корень будет лежать в первом
элементе массива, а сыновья i-ой вершины
будут лежать в элементах с номерами 2i
и 2i + 1 – левый и правый соответственно.
Сразу можно заметить очевидное свойство:
T[i] = min(T[2i], T[2i + 1]) для i-ой вершины, не
являющейся листом. Листы, к слову, будут
лежать при такой нумерации в элементах
с номерами от n до 2n – 1.
Назовём
фундаментальным отрезком в массиве
такой отрезок, что существует вершина
в дереве, которой он соответствует.
Разобьём наш отрезк на минимальное
количество непересекающихся
фундаментальных. Покажем, что на каждом
уровне их количество не превосходит
2.
Возьмём
самый большой фундаментальный отрезок
в разбиении. Пусть его длина – 2t. Заметим,
что фундаментальных отрезков длиной
2t – не более двух (1). Возьмём самый левый
из имеющихся максимальных фундаментальных.
Будем двигаться от него налево. Заметим,
опять же, что длины отрезков будут
убывать (2). Так же и с правым из максимальных.
Тем самым получим, что фундаментальных
отрезков – не более 2t, что не превосходит
2logn. Пункты (1) и (2) в доказательстве я
оставлю для самостоятельного
осмысления.
Чем нам это помогает?
Теперь мы можем реализовать запрос
минимума «снизу». Будем подниматься
снизу, добавляя к ответу на каждом
уровне, если надо, фундаментальный
отрезок.
Заведём два указателя – l и
r, с помощью которых будем находить
очередные фундаментальные отрезки
разбиения. Изначально установим l и r
указывающими на листы, соответствующие
концам отрезка запроса. Заметим, что
если l указывает на вершину, являющуюся
правым сыном своего родителя, то эта
вершина принадлежит разбиению на
фундаментальные отрезки, в противном
случае не принадлежит. Аналогично с
указателем r – если он указывает на
вершину, являющуюся левым сыном своего
родителя, то добавляем её в разбиение.
После этого сдвигаем оба указателя на
уровень выше и повторяем операцию.
Продолжаем операции пока указатели не
зайдут один за другой.
Находя очередной
фундаментальный отрезок, мы сравниваем
минимум на нём с текущим найденным
минимумом и уменьшаем его в случае
необходимости. Асимптотика работы
алгоритма – O(logn), т. к. на каждом уровне
мы выполняем константное число операций,
а всего уровней – logn.
int
rmq_up(vector<int>&
T,
int
l,
int
r)
{
int ans = INF;
int n = T.size() / 2;
l += n - 1, r += n - 1;
while (l <= r) {
if (l & 1) // если l - правый сын своего родителя,учитываем его фундаментальный отрезок
ans = min(ans, T[l]);
// если r - левый сын своего родителя,
// учитываем его фундаментальный отрезок
if (!(r & 1)) // если r - левый сын своего родителя учитываем его фундаментальный отрезок
ans = min(ans, T[r]);
// сдвигаем указатели на уровень выше
l = (l + 1) / 2, r = (r - 1) / 2;
}
return ans;
}
М одификация
Теперь
научимся изменять значение элемента
дерева. Заметим, что для каждого листа
есть ровно logn фундаментальных отрезков,
которые его содержат – все они
соответствуют вершинам, лежащим на пути
от нашего листа до корня.
Значит,
при изменении элемента достаточно
просто пробежаться от его листа до корня
и обновить значение во всех вершинах
на пути по формуле T[i] = min(T[2i], T[2i + 1]).
одификация
Теперь
научимся изменять значение элемента
дерева. Заметим, что для каждого листа
есть ровно logn фундаментальных отрезков,
которые его содержат – все они
соответствуют вершинам, лежащим на пути
от нашего листа до корня.
Значит,
при изменении элемента достаточно
просто пробежаться от его листа до корня
и обновить значение во всех вершинах
на пути по формуле T[i] = min(T[2i], T[2i + 1]).
void update(vector<int>& T, int i, int x)
{
int n = T.size() / 2;
i += n – 1;
T[i] = x;
while (i /= 2)
T[i] = min(T[2 * i], T[2 * i + 1]);
}
Ура! Получаем решение задачи Dynamic RMQ за (O(n), O(logn)).
Суффиксный массив
Дана
строка ![]() длины
длины ![]() .
.
![]() -ым суффиксом строки
называется подстрока
-ым суффиксом строки
называется подстрока ![]() ,
, ![]() .
Тогда суффиксным
массивом строки
.
Тогда суффиксным
массивом строки ![]() называется
перестановка индексов суффиксов
называется
перестановка индексов суффиксов ![]() ,
, ![]() ,
которая задаёт порядок суффиксов в
порядке лексикографической сортировки.
Иными словами, нужно выполнить сортировку
всех суффиксов заданной строки. Например,
для строки
,
которая задаёт порядок суффиксов в
порядке лексикографической сортировки.
Иными словами, нужно выполнить сортировку
всех суффиксов заданной строки. Например,
для строки ![]() суффиксный
массив будет равен:
суффиксный
массив будет равен:
![]()
Построение за ![]()
Строго
говоря, описываемый ниже алгоритм будет
выполнять сортировку не суффиксов,
а циклических
сдвигов строки.
Однако из этого алгоритма легко получить
и алгоритм сортировки суффиксов:
достаточно приписать в конец строки
произвольный символ, который заведомо
меньше любого символа, из которого может
состоять строка (например, это может
быть доллар или шарп; в языке C в этих
целях можно использовать уже имеющийся
нулевой символ). Сразу заметим, что
поскольку мы сортируем циклические
сдвиги, то и подстроки мы будем
рассматривать циклические:
под подстрокой ![]() ,
когда
,
когда ![]() ,
понимается подстрока
,
понимается подстрока ![]() .
Кроме того, предварительно все индексы
берутся по модулю длины строки (в целях
упрощения формул я буду опускать явные
взятия индексов по модулю). Рассматриваемый
нами алгоритм состоит из примерно
.
Кроме того, предварительно все индексы
берутся по модулю длины строки (в целях
упрощения формул я буду опускать явные
взятия индексов по модулю). Рассматриваемый
нами алгоритм состоит из примерно ![]() фаз.
На
фаз.
На ![]() -ой
фазе (
-ой
фазе (![]() )
сортируются циклические подстроки
длины
)
сортируются циклические подстроки
длины ![]() .
На последней,
.
На последней, ![]() -ой
фазе, будут сортироваться подстроки
длины
-ой
фазе, будут сортироваться подстроки
длины ![]() ,
что эквивалентно сортировке циклических
сдвигов. На каждой фазе алгоритм помимо
перестановки
индексов
циклических подстрок будет поддерживать
для каждой циклической подстроки,
начинающейся в позиции
с
длиной
, номер
,
что эквивалентно сортировке циклических
сдвигов. На каждой фазе алгоритм помимо
перестановки
индексов
циклических подстрок будет поддерживать
для каждой циклической подстроки,
начинающейся в позиции
с
длиной
, номер ![]() класса
эквивалентности,
которому эта подстрока принадлежит. В
самом деле, среди подстрок могут быть
одинаковые, и алгоритму понадобится
информация об этом. Кроме того,
номера
классов
эквивалентности будем давать таким
образом, чтобы они сохраняли и информацию
о порядке: если один суффикс меньше
другого, то и номер класса он должен
получить меньший. Классы будем для
удобства нумеровать с нуля. Количество
классов эквивалентности будем хранить
в переменной
класса
эквивалентности,
которому эта подстрока принадлежит. В
самом деле, среди подстрок могут быть
одинаковые, и алгоритму понадобится
информация об этом. Кроме того,
номера
классов
эквивалентности будем давать таким
образом, чтобы они сохраняли и информацию
о порядке: если один суффикс меньше
другого, то и номер класса он должен
получить меньший. Классы будем для
удобства нумеровать с нуля. Количество
классов эквивалентности будем хранить
в переменной ![]() .
.
П риведём пример.
Рассмотрим строку
риведём пример.
Рассмотрим строку ![]() .
Значения массивов
.
Значения массивов ![]() и
и ![]() на
каждой стадии с нулевой по вторую таковы:
на
каждой стадии с нулевой по вторую таковы:
Стоит
отметить, что в массиве
возможны
неоднозначности. Например, на нулевой
фазе массив мог равняться: ![]() .
То, какой именно вариант получится,
зависит от конкретной реализации
алгоритма, но все варианты одинаково
правильны. В то же время, в массиве
никаких
неоднозначностей быть не могло.
.
То, какой именно вариант получится,
зависит от конкретной реализации
алгоритма, но все варианты одинаково
правильны. В то же время, в массиве
никаких
неоднозначностей быть не могло.
Перейдём теперь к построению алгоритма. Входные данные:
char *s; // входная строка int n; // длина строки const int maxlen = ...; // максимальная длина строки const int alphabet = 256; // размер алфавита, <= maxlen
На нулевой
фазе мы
должны отсортировать циклические
подстроки длины ![]() ,
т.е. отдельные символы строки, и разделить
их на классы эквивалентности (просто
одинаковые символы должны быть отнесены
к одному классу эквивалентности). Это
можно сделать тривиально, например,
сортировкой подсчётом. Для каждого
символа посчитаем, сколько раз он
встретился. Потом по этой информации
восстановим массив
.
После этого, проходом по массиву
и
сравнением символов, строится массив
.
,
т.е. отдельные символы строки, и разделить
их на классы эквивалентности (просто
одинаковые символы должны быть отнесены
к одному классу эквивалентности). Это
можно сделать тривиально, например,
сортировкой подсчётом. Для каждого
символа посчитаем, сколько раз он
встретился. Потом по этой информации
восстановим массив
.
После этого, проходом по массиву
и
сравнением символов, строится массив
.
int p[maxlen], cnt[maxlen], c[maxlen];
memset (cnt, 0, alphabet * sizeof(int));
for (int i=0; i<n; ++i) ++cnt[s[i]];
for (int i=1; i<alphabet; ++i) cnt[i] += cnt[i-1];
for (int i=0; i<n; ++i) p[--cnt[s[i]]] = i;
c[p[0]] = 0; int classes = 1;
for (int i=1; i<n; ++i) { if (s[p[i]] != s[p[i-1]]) ++classes; c[p[i]] = classes-1;}
Далее,
пусть мы выполнили ![]() -ю
фазу (т.е. вычислили значения
массивов
и
для
неё), теперь научимся за
-ю
фазу (т.е. вычислили значения
массивов
и
для
неё), теперь научимся за ![]() выполнять следующую,
-ю,
фазу.
Поскольку фаз всего
выполнять следующую,
-ю,
фазу.
Поскольку фаз всего ![]() ,
это даст нам требуемый алгоритм с
временем
,
это даст нам требуемый алгоритм с
временем ![]() .
Для этого заметим, что циклическая
подстрока длины
состоит
из двух подстрок длины
.
Для этого заметим, что циклическая
подстрока длины
состоит
из двух подстрок длины ![]() ,
которые мы можем сравнивать между собой
за
,
которые мы можем сравнивать между собой
за ![]() ,
используя информацию с предыдущей фазы
— номера
классов
эквивалентности. Таким образом, для
подстроки длины
,
начинающейся в позиции
,
вся необходимая информация содержится
в паре чисел
,
используя информацию с предыдущей фазы
— номера
классов
эквивалентности. Таким образом, для
подстроки длины
,
начинающейся в позиции
,
вся необходимая информация содержится
в паре чисел ![]() (повторимся,
мы используем массив
с
предыдущей фазы).
(повторимся,
мы используем массив
с
предыдущей фазы).
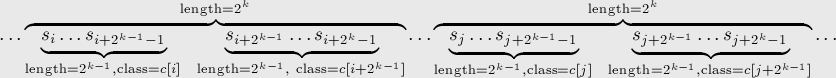
Это
даёт нам весьма простое
решение: отсортировать подстроки
длины
просто по этим парам
чисел,
это и даст нам требуемый порядок, т.е.
массив
.
Однако обычная сортировка, выполняющаяся
за время
,
нас не устроит — это даст алгоритм
построения суффиксного массива с
временем ![]() (зато
этот алгоритм несколько проще в написании,
чем описываемый ниже). Как быстро
выполнить такую сортировку пар? Поскольку
элементы пар не превосходят
,
то можно выполнить сортировку подсчётом.
Однако для достижения лучшей скрытой
в асимптотике константы вместо сортировки
пар придём к сортировке просто чисел.
Воспользуемся здесь приёмом, на котором
основана так называемая цифровая
сортировка:
чтобы отсортировать пары, отсортируем
их сначала по вторым элементам, а затем
— по первым элементам (но уже обязательно
стабильной сортировкой, т.е. не нарушающей
относительного порядка элементов при
равенстве). Однако отдельно вторые
элементы уже упорядочены — этот порядок
задан в массиве
от
предыдущей фазы. Тогда, чтобы упорядочить
пары по вторым элементам, надо просто
от каждого элемента массива
отнять
—
это даст нам порядок сортировки пар по
вторым элементам (ведь
даёт
упорядочение подстрок длины
,
и при переходе к строке вдвое большей
длины эти подстроки становятся их
вторыми половинками, поэтому от позиции
второй половинки отнимается длина
первой половинки). Таким образом, с
помощью всего лишь вычитаний от элементов
массива
мы
производим сортировку по вторым элементам
пар. Теперь надо произвести стабильную
сортировку по первым элементам пар, её
уже можно выполнить за
с
помощью сортировки подсчётом. Осталось
только пересчитать номера
классов
эквивалентности, но их уже легко получить,
просто пройдя по полученной новой
перестановке
и
сравнивая соседние элементы (опять же,
сравнивая как пары двух чисел).
Приведём реализацию выполнения
всех фаз алгоритма, кроме нулевой.
Вводятся дополнительно временные
массивы
(зато
этот алгоритм несколько проще в написании,
чем описываемый ниже). Как быстро
выполнить такую сортировку пар? Поскольку
элементы пар не превосходят
,
то можно выполнить сортировку подсчётом.
Однако для достижения лучшей скрытой
в асимптотике константы вместо сортировки
пар придём к сортировке просто чисел.
Воспользуемся здесь приёмом, на котором
основана так называемая цифровая
сортировка:
чтобы отсортировать пары, отсортируем
их сначала по вторым элементам, а затем
— по первым элементам (но уже обязательно
стабильной сортировкой, т.е. не нарушающей
относительного порядка элементов при
равенстве). Однако отдельно вторые
элементы уже упорядочены — этот порядок
задан в массиве
от
предыдущей фазы. Тогда, чтобы упорядочить
пары по вторым элементам, надо просто
от каждого элемента массива
отнять
—
это даст нам порядок сортировки пар по
вторым элементам (ведь
даёт
упорядочение подстрок длины
,
и при переходе к строке вдвое большей
длины эти подстроки становятся их
вторыми половинками, поэтому от позиции
второй половинки отнимается длина
первой половинки). Таким образом, с
помощью всего лишь вычитаний от элементов
массива
мы
производим сортировку по вторым элементам
пар. Теперь надо произвести стабильную
сортировку по первым элементам пар, её
уже можно выполнить за
с
помощью сортировки подсчётом. Осталось
только пересчитать номера
классов
эквивалентности, но их уже легко получить,
просто пройдя по полученной новой
перестановке
и
сравнивая соседние элементы (опять же,
сравнивая как пары двух чисел).
Приведём реализацию выполнения
всех фаз алгоритма, кроме нулевой.
Вводятся дополнительно временные
массивы ![]() и
и ![]() (
—
содержит перестановку в порядке
сортировки по вторым элементам пар,
—
новые номера классов эквивалентности).
(
—
содержит перестановку в порядке
сортировки по вторым элементам пар,
—
новые номера классов эквивалентности).
int pn[maxlen], cn[maxlen];
for (int h=0; (1<<h)<n; ++h) {
for (int i=0; i<n; ++i) {
pn[i] = p[i] - (1<<h);
if (pn[i] < 0) pn[i] += n;}
memset (cnt, 0, classes * sizeof(int));
for (int i=0; i<n; ++i) ++cnt[c[pn[i]]];
for (int i=1; i<classes; ++i) cnt[i] += cnt[i-1];
for (int i=n-1; i>=0; --i) p[--cnt[c[pn[i]]]] = pn[i];
cn[p[0]] = 0; classes = 1;
for (int i=1; i<n; ++i) {
int mid1 = (p[i] + (1<<h)) % n, mid2 = (p[i-1] + (1<<h)) % n;
if (c[p[i]] != c[p[i-1]] || c[mid1] != c[mid2]) ++classes;
cn[p[i]] = classes-1; }
memcpy (c, cn, n * sizeof(int));}
Этот
алгоритм требует
времени
и
памяти.
Впрочем, если учитывать ещё размер
алфавита,
то время работы становится ![]() ,
а размер памяти —
,
а размер памяти — ![]() .
.
Суффиксный бор
З
 аметьте,
что первым
суффиксом строки
называется эта строка без первого
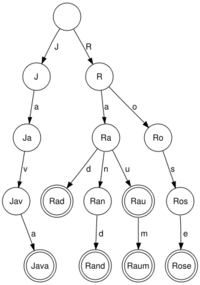
символа.Бор -
это дерево, составленное из набора
строк. На рисунке приведён пример бора
для строк "Java", "Rad", "Rand",
"Raum" и "Rose".
аметьте,
что первым
суффиксом строки
называется эта строка без первого
символа.Бор -
это дерево, составленное из набора
строк. На рисунке приведён пример бора
для строк "Java", "Rad", "Rand",
"Raum" и "Rose".
![]()
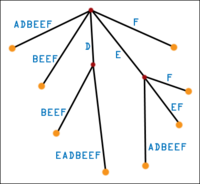
Несжатое суффиксное дерево - это бор, составленный из всех суффиксов данной строки.
Сжатое суффиксное дерево - это некоторая оптимизация несжатого дерева, в котором структуру из нескольких последовательных вершин, выглядящих как односвязный список, заменяют на одно ребро (см. рисунок). Заметим, что каждая из строчек, записанных на рёбрах, является подстрокой исходной строки и, следовательно, задаётся индексом первого и последнего символа. Поэтому память, занимаемую суффиксным деревом, можно оценить как O(n * r), где n - количество вершин в дереве, а r - количество букв в алфавите. В случае использования связных списков или мапов эту оценку можно уменьшить до O(n).
Свойство сжатого суффиксного дерева
Докажем
следующий факт: Количество
вершин в сжатом суффиксном дереве для
строки длины L не
превосходит 2L +
1.
Очевидно, что суффиксное дерево не
зависит от того, каким методом мы его
строим. Тогда рассмотрим "наивный"
алгоритм построения - будем добавлять
в дерево все суффиксы по очереди. При
добавлении каждого суффикса в дерево
добавляется не более двух вершин (одна
- за счёт того что мы могли разбить
какое-то ребро на два, и одна - лист,
соответствующий добавленному суффиксу).
т.к. суффиксов всего L (пустой суффикс
считать не будем), а изначально в дереве
всего одна вершина (корень), то
получаем ![]() ч.т.д.
Таким образом, сжатое суффиксное дерево
занимает память порядка длины строки.
Данное представление суффиксного дерева
было впервые упомянуто МакКрейтом в
1976 году.
ч.т.д.
Таким образом, сжатое суффиксное дерево
занимает память порядка длины строки.
Данное представление суффиксного дерева
было впервые упомянуто МакКрейтом в
1976 году.
Алгоритм построения сжатого суффиксного дерева за o(l)
Наивный алгоритм построения суффиксного дерева, описанный в доказательстве леммы о количестве вершин, работает в худшем случае за время O(L2 )Алгоритм построения суффиксного дерева за линейное время был придуман финским математиком Укконеном (Ukkonen) в 1995 году. Основывается он на следующих двух идеях:
Суффиксные ссылки
Каждой вершине в суффиксном дереве очевидно соответствует некоторая строка - путь из корня в эту вершину. Для корректно построенного суффиксного дерева выполнено следующее утверждение: если некотороя строка входит в дерево, то и все её суффиксы входят в это дерево. Можно показать, что для любой внутренней вершины дерева все суффиксы соответствующей строки также приводят в вершины. Основываясь на этом, можно ввести понятие суффиксной ссылки для любой внутренней вершины, кроме корня: Пусть вершине v соответствует строка s. Обозначим за t первый суффикс s (s без первой буквы). Тогда суффиксной ссылкой вершины v назовём ссылку ведущую в вершину, соответствующую строке t.
Быстрое нахождение суффиксных ссылок
П
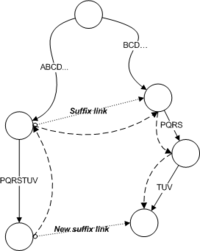 редположим,
что во время построения мы добавили в
дерево внутреннюю вершину. Теперь мы
хотим провести из этой вершины суффиксную
ссылку. Действуем следующим образом:
идём в предка (u) добавленной вершины
(v). Затем идём по суффиксной ссылке u →
u'. Далее находим в поддереве с корнем
u' строку, написанную на ребре u-v. Т.к.
такая строка в этом поддереве точно
есть, то нам не обязательно сравнивать
каждую букву - если мы находимся на
правильном ребре (первая буква ребра
совпала), то всё это ребро можно пройти
за время O(1). Таким образом попадаем в
некоторую вершину v', которая и будет
суффиксной ссылкой для вершины v. В том
случае если вершины v' не существует, то
необходимо её создать и повторить
вышеуказанную операцию. Для лучшего
понимания см. иллюстрацию:
редположим,
что во время построения мы добавили в
дерево внутреннюю вершину. Теперь мы
хотим провести из этой вершины суффиксную
ссылку. Действуем следующим образом:
идём в предка (u) добавленной вершины
(v). Затем идём по суффиксной ссылке u →
u'. Далее находим в поддереве с корнем
u' строку, написанную на ребре u-v. Т.к.
такая строка в этом поддереве точно
есть, то нам не обязательно сравнивать
каждую букву - если мы находимся на
правильном ребре (первая буква ребра
совпала), то всё это ребро можно пройти
за время O(1). Таким образом попадаем в
некоторую вершину v', которая и будет
суффиксной ссылкой для вершины v. В том
случае если вершины v' не существует, то
необходимо её создать и повторить
вышеуказанную операцию. Для лучшего
понимания см. иллюстрацию:
Дополнительная вершина
Для упрощения реализации полезно ввести дополнительную вершину, в которую будет вести суффиксная ссылка из корня, и из которой в корень будут вести всевозможные однобуквенные рёбра.
Алгоритм Укконена
Алгоритм Укконена строит суффиксное дерево, добавляя в него по одной букве. Текущая позиция в дереве соответствует максимальному неполному суффиксу уже добавленных букв, который уже встечался где-то раньше. Так, для строки aaababaab таким суффиксом будет aab. Псевдокод добавления буквы в дерево выглядит следующим образом:
пока из текущей позиции нельзя сходить по данной букве
| если нет вершины в текущей позиции
| | добавить вершину и построить суффиксную ссылку
| +-------
| пройти по суффиксной ссылке
+---------
сходить по данной букве
При этом на рёбрах, ведущих в листья, индекс последней буквы надо проставлять
