
Граничные условия
Очевидно, эм поле распространяется в среде и может встретить др среды и др вещества. Граница раздела сред существенно влияет на процесс прохождения эм волны по этой среде (оконное стекло и зеркало). Для ответа на вопрос: как поле ведет себя на границе раздела двух сред, существуют в эд граничные условия. В отличие от материальных уравнений, граничные условия следуют из ур-ий Максвелла. Если их записать для маленького цилиндра, либо для прямоугольной площадки и затем перейти к пределу, когда Δh→0. Цилиндр применяется для уравнений с div, 2 объект для ур-ий с rot.
 |s
=
|s
=
 (1)
(1)
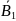 |s
=
|s
=
 (2)
(2)
Из
ур-ий для div
получаются следующие граничные условия
для нормальных компонент полей

 s
= 0
(3)
s
= 0
(3)
 s
=
s
=
 (4) ,
- поверхностная плотность заряда
(4) ,
- поверхностная плотность заряда

 (5)
(5)
Из ур-ий для rot получаем следующие граничные условия на тангенсальные соответствующие полей и :
 s
= 0
(6)
s
= 0
(6)
 s
=
s
=
 (7)
– поверхностная плотность тока
(7)
– поверхностная плотность тока
 (8)
(8)
Лекция №5
Комплексные амплитуды
В ЭД переменных полей широко используются комплексные амплитуды. Дело в том, что в СВЧ наибольший интерес представляет специальный случай зависимости поля от времени, которые называется гармонической зависимостью и имеют вид:
 (1)
(1)
Cos и sin – гармоническая функция. Такая же зависимость (1) справедлива и для других компонент полей.
 - круговая частота [
- круговая частота [ =2
=2 (2)
(2)
 Т=
Т=
Векторное гармоническое поле можно представить в следующем виде:
 (3) фаза учтена
автоматически.
(3) фаза учтена
автоматически.
Мы будем работать, фактически, только с такими полями частотой .
Отступление
Коммутативность операций real Z и …
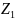 и
и



 и
и

 =
=
Рассмотрим
сигнал
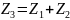
Процедура перехода комплексного поля в реальное


 =
= +
+
+
+
 +
-
+
-
 +
+

При рассмотрении в линейных средах комплексных полей, опреация прехода…..
Э то
означает, что мы можем от реального
сигнала, описываемого величиной x
, перейти….
то
означает, что мы можем от реального
сигнала, описываемого величиной x
, перейти….
Х → Z
→ Z

 →
→

При рассмотрении гармонических полей удобно пользоваться комплексным представлением этих полей, а именно представим (3) в сл виде:
 (4)
(4)
 - комплексная
амплитуда
- комплексная
амплитуда
 (
( )
=
)
=
 (
)
+i
(
)
+i
 (
)
(5)
(
)
(5)
Линейная связь или комбинация, включающая гармонические поля, приводит к линейной же связи для комплексных амплитуд. Нелинейные же операции требую тщательного рассмотрения.
Правило действия с комплексными векторами совпадает с правилами действия над обычными векторами, с учетом алгебры комплексных чисел; i рассматривается как число.
Пример:
 +i
)
+i
)
+i
)
+i
)
 + i
+ i
 -
-
 i 2
i 2
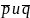 - вещественные вектора
- вещественные вектора
 +i
)
-i
)
=
+i
)
-i
)
=
 - вещественное или действительное
- вещественное или действительное
До сих пор мы работали с вещественными эм полями. Перейдем к комплексным полям.
 (6)
(6)
В чем преимущество введения комплексных полей? Только в одном – дифференциальные зависимости от времени комплексных полей превращается в алгебраические зависимости комплексных амплитуд.

 +3
+3 + 4
+ 4
 =
(7)
=
(7)

(7’)

 (8)
(8)
