
Лекция №1
Введение
ЭД СВЧ изучает вопросы, связанные с распространением эм волн высокой частоты (100МГц-10ГГц) в стр-ах, имеющих выделенное направление распространения. Этот курс важен с точки зрения мат аппарата, необходимого для изучения эм процессов в различных стр-ах. ЭД СВЧ имеет дело сразу с эм полем.(по-сравнению с эл.магнитизмом). Эм поле оказывает силовое (иногда разрушительное) действие на материалы (лазерная резка тв материалов, лазерное оружие и т.д).
С точки зрения мат-ки, поле – это любая функция пространственных координат(время). Эта функция может быть сколярной(т.е.не зависеть от направления), векторной либо тензорной.
Определение векторов эм поля
Основная задача эд: нахождение векторов эм поля в каждой точке пространства для любого момента времени, если заданы источники эм поля, либо значение поля на какой-то границе.
Мы определим хар-ки
эм поля по силовому воздействию этого
поля на пробную частицу, имеющую заряд
q и движущуюся со скоростью
 .
Эм поле хар-ся двумя векторами:
.
Эм поле хар-ся двумя векторами:
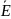 (
( ,t)
и
,t)
и
 (
,t),
с помощью которых опр-ся сила, действующая
на эту частицу:
(
,t),
с помощью которых опр-ся сила, действующая
на эту частицу:
 =q(
+
x
)
(1) Сила Лоренца
=q(
+
x
)
(1) Сила Лоренца
( ,t) – вектор электрической напряженности эм поля
( ,t) – вектор маг индукции эм поля
– единственное определение векторов поля и
СВЧ излучение резонансно воздействует на вращательные степени свободы молекулы, т.е. заставляет вращаться части молекул. При вращении происходит поглощение. Принцип работы СВЧ.
Лекция №2
Мат-ое введение в курс эд свч
В эд существенно используют векторный анализ
Элементы векторного анализа
Рассмотрим все процессы в декартовой системе координат. В других сис-ах координат эти понятия надо будет видоизменять.

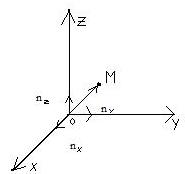 =
(x,y,z)
=
(x,y,z)
=x +y
+y +z
+z (1) эти векторы безразмерны
(1) эти векторы безразмерны
При мат описании физ-их полей недостаточно только алгебраических выражений, мы обязаны применять более сложные мат операции (диф-ие, инт-ие и т.д.).
 =
= (2)
(2)
 =
=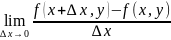 (5)
(5)
Частная производная: фиксируется константа и производится диф-ие.
f(x,y)
=
 = 2x
= 2x
В эд встречаются более сложные операции диф-ия: градиент от скалярной функции:
grad
 (
)
– это вектор
(
)
– это вектор
div )
– это скаляр
)
– это скаляр
rot (
)
– это вектор
(
)
– это вектор
rotrot - это вектор
grad(div ) – это вектор
Δ
=
 (лапласян)
(лапласян)
Для удобства работы введем понятие оператор.
Говорят, что на
пространстве
 (это пространство дважды непрерывная
диф функция пространственных координат)
задан оператор Â,если любая
(это пространство дважды непрерывная
диф функция пространственных координат)
задан оператор Â,если любая
 ставится в соответствие другая функция
ставится в соответствие другая функция

Â=
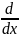
 =
=

Если

ĤΨ=EΨ – собственная функция оператора.(должно быть ℋ)
Ĥ =
 +U(
)
+U(
)



Введем
основной оператор - оператор набла
- сконструирован из операторов типа

=
+

 (7)
(7)
=
 +
+
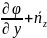
 (8)
(8)
Градиент функции:
grad = Right(8)
=
 grad
= 2x
grad
= 2x
grad( +
+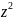 /=grad(
/=grad( )
Ψ
)
Ψ ))
– найти градиент от произведения
скалярных полей =
))
– найти градиент от произведения
скалярных полей =

 (9)
(9)
I способ: основан на явном виде (7) с некоторыми преобразованиями в духе Эйнштейна.
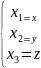 (10)
(10)
=

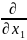 +
+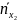
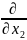 +
+
 =
=
 =
=


Эйнштейн ввел правило, что если в выражении 2 раза встречается одинаковый индекс, то под ними понимается суммирование по всей области изменения индекса:
 =
=

(Замечание: это правило работает, если этого индекса нет слева).
grad
=

grad
=
 = /
=(
= /
=(
 )
) /=
/=
 (
)
(
) +
+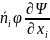 = =
= =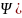 )
+
)
+
 )
=
)
=

