10.Теорема о моментах инерции относительно паралельных осей. Моменты инерции простейших тел.

Теорема Штейнера. 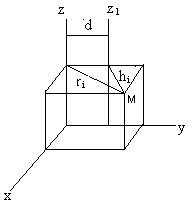I_z=Σm_i*r_i²=ΣM_i(x_i²+y_i²); I_z=Σm_ih_i²=Σm_i[x_i²+(y_i-d)²]= =Σm_i(x_i²+y_i²)+d²Σm_i=I₀+M*d² Момент инерции механической системы относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс системы, сложенному с произведением массы всей системы на квадрат расстояния между осями. J=J₀+M*d²

М. и. однородного тонкого стержня

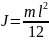
М. и. однородной круг. пластинки малой толщины

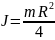
М. и. однородного круг. цилиндра

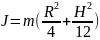
М. и. полого цилиндра

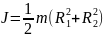
М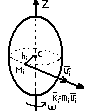 . и. однородного кругового конуса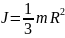

М. и. однородного шара

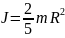
11.Теорема о движении центра масс мех. Сист. Законы сохранения центра масс.

Центр масс механической системы движется как материальная точка с массой равной массе всей системы под действием главного вектора внешних сил.

1) если R^e=0,то а_с=dV_c/dt=0. V_c=const, следовательно движение прямолинейное и равномерное. Если главный вектор внешних сил действующий на систему равен 0,то центр масс этой системы, либо покоится, либо совершает равномерное прямолинейное движение. R_x^e=0,то а_сx=dV_cx/dt=0. V_cx=const,следовательно движение равномерное. В случае если V_cx=0,то V_cx=dx_c/dt=0 или x_c=const.

12.Кол-во движения т. и системы. Теорема об изменении кол-ва движения мат. т. и мех. системы. Законы сохранения кол-во движения.

1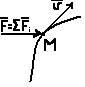 ) Количество движения есть векторная величина, которая является мерой механического движения точки или системы. Для точки вектор количества движения определяется как произведение её массы на вектор скорости 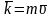Вектор 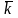направлен по касательной к траектории, так же как и вектор 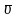Для механической системы

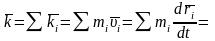
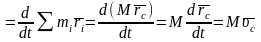
Количество движения механической системы есть мера поступательного характера механического движения.

2) Теорема об изменении количества движения точки (дифференциальная форма)

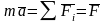
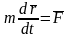
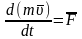
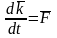где 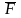равнодействующая всех сил, действующих на точку. В случае движения мех. системы при рассмотрении всех сил, действующих на эту систему учитываются только внешние силы, т.к. главный вектор внутренних сил системы всегда =0. Поэтому для мех. системы указанная теорема примет вид: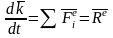 Производная по времени от вектора количества движения мех.системы равна главному вектору внешних сил, действующих на систему.

3)Следствия теоремы: (закон сохранения количества движения)

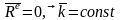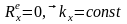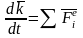
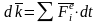
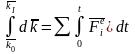
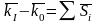Если 2) Если 3) Теорема об изменении количества движения мех.системы (интегральная форма) (теорема импульсов) Рассмотрим движение мех.системы под действием совокупности внешних сил. Справедливо будет: Изменение количества движения мех.системы за некоторый промежуток времени равно суммарному импульсу всех внешних сил, действующих на систему за тот же промежуток времени.