Конечные автоматы.Представление автомата орг. Графом, взвешанным над п/к регулярных языков.

Автомат-устройство, сост. Из блока управления входной ленты, головки автомата и блока внутр. памяти автомата.

…

а

…

…

Головка автомата

Блок управления

Внутр. память автомата.

Лента ,которая предполагается полубесконечной(не огр.справа) и разумна на ячейке;записываются во входном алфавите .цепочку записанную таким образом на вх. ленте авт. будем наз. входной цепочкой.

Блок управления может в каждый момент времени находится в одном из конечного множества состояния.

Пусть в некоторый момент времени автомат обозревает какую-то ячейку ленты, а БУ находится в некотром состоянии qQ.Такт работы автомата состоит в ячейке, состояние q, а так же содержимого внут. памяти автомат сдвигает головку вправо или влево на одну ячейку либо оставляет её на прежнем месте, его БУ переходит в некоторое некоторое новое состояние r,а содержимое внутр. памяти меняется.

Вводят понятие конфигурации автомата: она представляется состоянием блока управления, содержимым обозреваемой ячейки и содержимое внутр. памяти.

Конечные автоматы-это анализирующие модели для РЯ. КА не имеет внутр. памяти, головка движется по ленте только вправо-на 1 ячейку за такт.с ленты можно только читать. Кроме того,автомат может переходить «спонтанно» из одного состояния в другое, не читая ленту и не продвигая головку-переход в состояние по пустой цепочке.

Кофигурация КА-упорядоченная пара(q,ay),q-сост БУ,а-символ в обозреваемой ячейке,у-цепочка во входном алфавите, расп. в ячейках справа от обозреваемой.

КА- это орг. граф размеченный над п/к R(V) в алфавите V с выделенной вершиной q₀ подмножеством вершин F.

М=(Q ,E, ,q₀,F)

Q-мн-во состояний автомата

Е-мн-во дуг

Фи-функция разметки

q₀- нач. сост.

F-подмножество закл сост.

14.1..Замкнутое полукольцо.Непрерывность операции сложения в замнкутом полукольце.Теорема о наименьшем решении линейного уравнения х=ах+b в замкнутом п/к.

Замкнутое п/к-$=(S,+,.,0,1I):

1)оно идемпотентно

2)любая посл-ть эл-тов мн-ва S имеет т.в.г.относительно естественного порядка  этого идемпотентного п/к. , x_iS sup )

3)операция «.» сохраняет т.в.г. последовательности

 nN

a sup = sup

sup = sup

Теорема: конечное идемпотентное п/к замкнуто

Док-во: поскольку носитель S идемп. п/к S=(S,+,.,0,1I) есть конечное множество,то множество эл-ов  последовательности в этом п/к конечно.Для нахождения точной верхней грани такой последовательности нужно найти точную верхнюю грань мн-ва р= ее членов,т.е. согласно теор.,вычислить некоторую конечную сумму, которая всегда .Таким образом, в кот.

идемпотентном п/к  последовательность имеет т.в.г.

Условия хранения точных верхних граней имеют вид

a(p₁+…p_n)=ap₁ +…+ap_n

(p₁+…+p_n)*a=p₁a+…+p_na S-п/к замкнуто

Базис Жегалкина и его полнота. Полином Жегалкина. Теорема о единственности

полинома Жегалкина для каждой булевой функции

Базис Жегалкина – полное множество БФ {(+), . , 1}

Полином Жегалкина – формула вида a0+a1x1+a2x2+…+anxn+a12x1x2+…+a12…n x1…xn

Т-ма: для каждой БФ полином Жегалкина определён однозначно.

Д-во: Посчитаем кол-во коэф-тов в полиноме Жегалкина от n перем. Заметим, что каждый коэф-т ai1…in <-> {i1…in}=c{1…n} (ставится в соответствие)

• |2^({1…n})| = 2^n {0,1}

• Различных БФ от n перем можно задать с помощью полинома Жегалкина 2^((2^n)), что совпадает с кол-вом БФ от n переем

• Для каждой БФ существует однозначно определённый полином Жегалкина.

Полином жегалккина над x_1….x_n называется выражение вида к₁+к₂…+к_е, е1 и все к_i различные монотонные коньюкции над x₁…x_n,либо конст.

Теор Жигалкина:Любую функцию алгебры логики f(x₁…x_n) можно единственным образом выразить полиномом жегалкина над x₁…x_n

До-во:1)Докажем  полинома, система 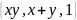полна, функцию алгебры логики f(x₁…x_n) можно реалиховывать формулой над

А)Пользуясь дистрибутивностью раскрываем все скобки в этой реализации и получаем ,что f(x₁…x_n) = к₁+к₂…+к_i ,где к_i –коньюкция переменных и единицу.

Б)преобразуем все полученные коньюкции в элементарные,пользуясь при этом коммутативностью о соотношениями х*х=х, 1*1=1, А*1=А.Очевидно,все коньюкции станут монотонными.

В)преобразуем полученную сумму в полином жегалкина ,пользуясь при этом соотношениями А+а=А и А+0=А в результате получим либо k_i1 + k_i2 +…+ k_in либо конст 0

	Х1	Х2	Х3	Х
Х1х2х4	1	1	0	1
Х2х3	0	1	1	0
1	0	0	0	0

2)Докажем единственность представления .Подсчитаем число различных всевозможных монотонных коньюкций от n переменных.Для этого сост табл

	ху	х	у	1
Ху+1	1	0	0	1
0	0	0	0	0

вида,где каждой переменной соотв. 1,если она присутствует в монотонной коньюкции 0 в противном случае.При этом конст.1 поставим в соотв нулевой набор.Очевидно,что построенное отображение биективно,всего тразличных монотонных коньюкций от n переменных 2ⁿ. Построим аналогичное биективное отображение между всевозможными суммами монотонных коньюкций и векторами длинн 2ⁿ -числа коньюкции.Для этого составим

табл вида ,где под соотв. Монотоной коньюкции стоит эдиница если она входит в данную суммму и ноль, если не входит.При этом константе 0 ставится в соотв нулевой набор.Очевидно,отображение биективно.Всего таких различных сумм будет столько сколько  различных булевых векторов длины 2ⁿ,т.е. 2 ⁿ .Мы получим,что число различных полиномов Жегалкина совпадает с числом функций алгебры логиги.Поскольку отображение из мн-ва полиномов во мн-во функций сюрьективно то оно и биективно над n переменными и функций алгебры логиги от n переменных равномощны.Единственность доказанна.

15.1.Задача о путях во взвешанных графах. Утверждение о вычислении стоимости прохождения по всем путям длины L.Среди задач анализа ор. Графов весьма важны след. Задачи:1)Вычисление для заданного ор, графа его матрицы достижимости. Это задача построения транзитивного замыкания ор. графа. Матрицу достижимости можно рассматривать как матрицу транзитивного и рефлексивного замыкания б.о. непосредственной достижимости в ор. Графе.2)Вычисление таких расстояний между всеми парами вершин в ор. Графе. Это задача о кратчайших расстояниях.3)Перечисление всех путей между двумя произвольными вершинами. Задача о перечисление путей. 3)Метка пути ведущего из вершин v_i в вершину vj , есть произведение в п/к В меток входящих в путь дуг в порядке их следования (для пути ненулевой длины) и есть1I(единица п\к /r ) для пути нулевой длины. Стоимость прохождения из вершин v_i в вершину v_j -это сумма в п\к R меток всех путей, ведущих из вершины v_i в вершину v_j .Лемма. Элемент a^{( e)}_ij матрицы A^e,e0 равен стоимости прохождения из вершины v_i в вершину v_j по всем путям длины L.Док-во: доказательство проведем индукцией по L. При l=e утверждении очевидно, т.к. A=E , Е-единичная матрица, которая матрицей стоимости прохождения по всем путям длины О. l=1: a^{( e)}_ij = a^(e-1)_ik a_ki .Cогласно предложению индукции, элемент a^(e-1)_ik равен стоимости прохождения из вершины v_i в вершину v_j по всем путям длины L-1. Множ. Всех путей длины L из вершины v_i в вершину v_j , проходящих через фиксированную k-ю вершину так, что вер. V_k Связанных с другой вер. V_j Образуется путем присоединения дуги (V_k, V_j) к каждому из путей, ведущих из v_i в v_k и имеющих длину L-1. Тогда видно, что написанное выше выражение для элемента a^{( e)}_ij дает стоимость прохождения из вершины v_i в вершину v_j по всем путям длины L .Т.К. стоимость прохождения между парой вершин v_iv_j равна сумме меток всех путей, ведущих из первой вершины во вторую, а указанную сумму можно получить, послед. Метки путей длины 0,1,2…, то матрица стоимостей взвеш. Ор.графа с учетом леммы может быть представлены в виде:c=A⁰ +A¹+A²…+Aⁿ+= =A*

.. Теорема о равенстве порядка конечной циклической группы порядку группы.

Полугруппу (в частности группу) (А, .) наз циклической, если сущ такой эл-т а, что любой эл-т х полугруппы является некоторой степенью эл-та а. Эл-т а наз образующим эл-том полугруппы (группы).

Порядок конечной группы – кол-во эл-тов в этой группе

Порядок эл-та а циклической группы – наименьшее положительное n такое, что а^n=1.

Теор: Порядок образующего эл-та конечной циклической группы равен порядку самой группы.

Д-во: Пусть G=(G, . , II) – конечная циклическая группа с обр эл-ом а, и n>0 – порядок этого эл-та.

Тогда все степени а^0=II, a^1=a, a^(n-1) попарно различны. Действительно, если a^k = a^l, 0<l<k<n, то a^(k-l) = a^(k+(-l)) = a^k*a^(-l) = a^(l-l)=II. Поскольку k-l<n, получено противоречие с выбором n как порядка эл-та а (ибо найдена степень меньше n, при возведении в которую эл-та а получится единица).

Осталось доказать, что любая степень эл-та а принадлежит множеству {I, a, a^(n-1)}. Поскольку каждый эл-т группы G есть некоторая степень эт-та а, то G={1, a, ,,,a^(n-1)}, и порядок группы = n.

Из док-ва теоремы следует, что в бесконечн цикл группе не сущ n>0, что для образующего эл-та а группы вып-ся рав-во a^n=I.

.точная верхняя грань последовательности.Индуктивное упорядоченной множество.Непрерывное отображение.Монотонное отображение.Теорема о монотонности непрерывного отображения.пример монотонного отображения,не явл непрерывным.

Эл-т а упорядоченного мн-ва(М,) наз точной верх гранью последовательности 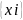_iN ,если он есть т.в.г. мн-ва всех членов пос-ти. Т.В.Г.по-ти есть т.в.г. области ее значений как функции натурального аргумента. Упорядочченное мн-во(М,) наз индуктивным ,если:1)оно содержит наименьший эл-т;2)всякая неубывающая пос-ть эл-ов этого мн-ва имеет т.в.г.

Пусть (М₁,) и (М₂,) –индуктивные упорядоченные мн-ва.Отображение f:М₁-М₂ одного индуктивного упорядоченного мн-ва в другое наз непрерывным.,если для любой неубывающей последовательности а₁…,а_n,… эл-ов мн-ва М₁ образ её т.в.г. равен т.в.г. пос-ти образов f(а₁),…,f(а_n)…,т.е.справедливо равенство f(sup a_n)=sup f (a_n).

Отображение f:M₁М₂ упорядоченных мн-в(М₁,) и (М₂,) наз монотоными,если а,bM из аbf(a)f(b)

Теорема:всякое непрерывное отображение одного индуктивного упорядоченного мн-ва в другое монотонно.

Док-во:пусть f-непрерывное отображение индуктивного уопрядоченного мн-ва (М₁,) в индуктивное упор. мн-во (М₂,).Пусть а,bM и аb.Образуем последовательность неубывающая для нее sup x_n=sup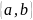 =b.В силу непрерывности отображения f. f(b)=f(supx_n)=f(sup )= sup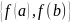 откуда следует, что f(a)f(b).Эл-т а мн-ва А наз. неподвижной т-кой отображения f:AA ,если f(a)=a.Эл-т упорядоченного мн-ва М наз наименьшей неподвижной не подвижной точ-кой отображения f:MM,если он явл. наименьшей эл-ом мн-ва всех неподвижных точек отображения f.

Теорема:любое непрерывное отображение f индуктивно упорядоченного мн-ва(М,) в себя имеет наименьшую неподвижную т-ку. Доказательство: обозначим через О наименьший элемент множества М. Полагаем f⁰(х)=х и fⁿ(х)= f(f^n-1(х)) для любой n˃0, т.е. fⁿ(х) означает результат n-кратного применения f к х. Рассмотрим последовательность элементов М: {fⁿ(0)}n≥o ={0,f(0), … fⁿ(0) …}. Докажем, что последовательность неубывающая. Используем метод математической индукции. Для элемента О, как наименьшего элемента множества М, имеем 0=f⁰(0)≤f(0). Пусть для некоторых натуральных n верно соотношение f^n-1(0)≤fⁿ(0), согласно теории о «отображении одного индуктивного упорядоченного множества в другом монотонно», отображение f монотонно, и по этому fⁿ(0)=f(f^n-1(0))≤f(fⁿ(0))=fⁿ⁺¹(0),т.е. соотношение верно для номера n+1. Согласно методу математической индукции, fⁿ(0)≤fⁿ⁺¹(0) для любого nEN₀, т.е. последовательность неубывающая. Следовательно, по определению индуктивного упорядоченного множества, она имеет точную верхнюю грань. Обозначим ее через а:а=sup_n≥0fⁿ(0). Докажем теперь, что если у неубывающей последовательности отбросить любое конечное число начальных членов, то ее точная верхняя грань не изменится. Действительно, если а есть точная верхняя грань неубывающей последовательности {х_n}≥0, то а≥х_n для всякого n≥0. В частности фиксируя производную к˃0, для любого n≥к имеем а≥х_n, т.е. а будет верхней гранью подпоследовательности {х_n}n≥k≥0.

Теорема о монотонности непрерывного отображения. Пример ионотонного отображения, не являющегося непрерывным.

Ф-ка: всякое непрерывное отображение одного упорядоченного индуктивного множества в другое монотонно.

Д-во: Пусть f – непрер отображ инд упор множества (М1, =<) в инд упор множество (М2, =<). Пусть a,b э М1 и a=<b. Образуем последовательность {Хn}n э N, где х1=а, хn=b, n>=2. Это последовательность неубывающая. Для неё supХn=sup{a,b}=b. В силу непрерывности отображения f f(b)=f(supXn)=f(sup{a,b})=sup{f(a),f(b)}, откуда следует, что f(a)<=f(b).

Рассмотрим множество всех точек отрезка [0,1] числовой прямой с порядком, индуцированным естественным числовым порядком. Это м-во индуктивно: его наим. эл-т 0, а люб неубыв послед-ть эл-в ограничена сверху и по признаку Веберштрасса имеет предел, который и будет её ТВГ.

Пример: f={0.5x 0<=x<=0.5

0.5+0.5x 0.5<=x<=1 }

Это отображение монотонно. Для последовательности {Хn}={n/(2n+1)}n э N ТВГ=0.5. ТВГ послед {f(Хn)}=0.25, a f(supXn)=f(0.5)=0.75. Следовательно отображение не является непрерывным в силу опр 1.5

1.5 Пусть (М1, =<) и (М2, =<) – индуктивные упорядоченным м-ва. Отобр f: М1->М2 наз непрерывным, если для люб неубыв послед a1…an… эл-тов м-ва M1 образ её ТВГ равен ТВГ послед образов f(a1)…f(an)…, т.е. справедливо ра-во f(supan)=supf(an).

Отображение f: М1->М2 упор м-в (М1, =<) и (М2, =<) наз монотонным, если из люб a,b э М1 из a=<b следует f(a)<=f(b).

Упор м-во(М, =<) наз индуктивным, если 1)оно содержит наим эл-т; 2)всякая неубыв послед-ть этого м-ва имеет ТВГ.