Регулярные языки.Индуктивная процедура порождения регулярных языков.Регулярные выражения.Полукольцо регулярных языков.Незамкнутость полукольца регулярных языков.

П/к РЯ-R(v) п/к с итерацией состоит из пустого языка языка 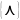,всех языков ,а(каждый из которых содержит единственную однобуквенную цепочку а),и замкнутую относительно итерации.

Теор. Язык в алфавите V регуляренон является элементом п/к R(v).Алгебраические операции над регулярными языками представляют с помощью регулярных выражений. Каждый р.в. представляет некоторой р.я., причем языки , и ,где а,обозначаются выражениям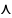и , и 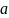,соответственно, и если рег. Выражение р обозначает р.я. Р, а рег. выражениями q обоз. р.я. Q, то (р+q),pq или p* обозначает множества pq, PQ и P*.

Приоритет.

:*,.,+.

V= -р.я.

1), , ,а

2)L₁ иL_2-р.я. L₁ L₂-р.я.

3) L₁0L₂-р.я.

4)L-р.я. L*= =р.я.

5)других нет.

.Алфавит.слово и язык в алфавите.полукольцо языков,его замкнутость.

Алфавит-это произвольное непустое конечное мн-во V=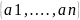 ,элементы кот. Наз. буквами или символами.

Слово- произвольный кортеж из мн-ва V^k(к-ый декартовый степени алфавита V)для различных к=0,1,2…

Язык – произвольное подм-во мн-ва V*

Соединением слов х=х(1)х(2)…х(к)и y=y(1)y(2)…y(m)наз слово

Xy=x(1)x(2)….x(k)y(1)y(2)….y(m)

Соединением языков L₁ иL₂ наз язык L1 L2,состоящий из всех возможных соединений слов ху,в кот. слово х принадлежит первому, а слово у-второму языку,т.е. L₁иL₂=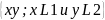

Итерация языка L наз. объединение всех его степеней:

L*=V_n=0 Lⁿ

П/к рег. Языков.В замкнутом п/к L(V) всех языков в алфавите V рассмотрим подалгебру, порожденную мн-вом, кот. Состоит из пустого языка, языка ,всех языков , а(каждый из которых содержит единственную однобуквенную цепочку а),и замкнутую относительно итерации.Эта подалгебра R(V),есть

п/к с итерацией.оно и есть п/к рег.языков.

Теорема о регулярности дополнения регулярного языка.Регулярность пересечения,разности и симметрической разности регулярных языков.

Теор: Дополнение регулярного языка есть регулярный язык.

Д-во: Пусть L-ря в алфавите v.Тогда дополнение языка L(как мн-ва слов) есть язык I=V*/L.

Согласно торемы о детерминизации для L может быть построен детерминизированным КА М, допускаемый L.Поскольку в детерминизированном автомате из каждой вершины по каждому входному символу определен переход в точности в одну вершину, то какова бы не была цепочка х в алфавите V для нее найдется единственный путь в М,нач. в начальном состоянии,на которой читается цепочка Х. Ясно ,что цепочка Х допускается автоматом М, т.е. хL(M),последнее состояние указанного пути явл. заключительным. Отсюда ,что цепочка хL(M)когда последнее состояние указанного пути не заключ.

Но наш как раз и нужен КА М,который допускает исходный исходный КА М превращая каждое заключительное состояние М в незаключетельное и наоборот, получим детерминизированный автомат,допускаемый дополнение языка L.

Для  двух РЯ L₁ и L₂ справедливы следующие утверждения:1)Пересечение L_{1 } L₂ регулярно

2)разность L_{1 /} L₂ регулярно

3)симм. разность L₁ 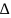L₂ регулярно.

Док-во:1) L_{1 } L₂₌ L_{1 }L₂

2) L_{1 /} L_{2 =} L_{1 } L₂

3) L₁ L₂₌ (L_{1 }L₂)( L_{1 } L₂)

Согласно определению(L КА М₁ и М₂ наз. эквивалентными если их языки совпадают),КА эквиваленты если допускаемые ими языки совпадают. Поэтому чтобы убедится в эквивалентности автоматов М₁ и М₂ достаточно доказать,что симметрическая разность языковL(M₁) и L(M₂) пуста. Для этого в свою очередь, достаточно построить автомат, допускающий эту разность и убедится в том, что допускаемый им язык пуст. В общем случае проблему распознавания того, что язык КА пуст, называют проблемой пустоты для КА. Чтобы решить эту проблему, достаточно найти множество заключенных состояний автомата,достижимых из нач. состояния.т.к. КА-это ориент. граф, то решить такую проблему можно с помощью поиска в ширину. Язык, допускаемый КА, пуст  мн-во заключительных состояний, достижимых из исп. сост., пусто. Практически эквивалентность КА предпочтительнее распозновать, исп. алгоритм минимизации.

10.1.Замкнутое полукольцо.Непрерывность операции сложения в замнкутом полукольце.Теорема о наименьшем решении линейного уравнения х=ах+b в замкнутом п/к.

Замкнутое п/к-$=(S,+,.,0,1I):

1)оно идемпотентно

2)любая посл-ть эл-тов мн-ва S имеет т.в.г.относительно естественного порядка  этого идемпотентного п/к. , x_iS sup )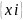

3)операция «.» сохраняет т.в.г. последовательности

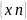 nN

a sup = su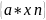p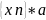

sup = sup

Теорема: конечное идемпотентное п/к замкнуто

Док-во: поскольку носитель S идемп. п/к S=(S,+,.,0,1I) есть конечное множество,то множество эл-ов  последовательности в этом п/к конечно.Для нахождения точной верхней грани такой последовательности нужно найти точную верхнюю грань мн-ва р=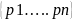 ее членов,т.е. согласно теор.,вычислить некоторую конечную сумму, которая всегда .Таким образом, в кот.

идемпотентном п/к  последовательность имеет т.в.г.

Условия хранения точных верхних граней имеют вид

a(p₁+…p_n)=ap₁ +…+ap_n

(p₁+…+p_n)*a=p₁a+…+p_na S-п/к замкнуто

Дизъюнктивные и конъюктивные нормальные формы. СДНФ и СКНФ. Теорема о представлении булевой функции в виде СДНФ и СКНФ.

Любая формула х или !х над стандартным базисом, где х – произвольная переменная, называется литералом.

Пусть ~xi – литерал. Ф-ла видa ~x1/\~x2/\…/\~xk наз-ся элементарной конъюкцией

~x1\/~x2\/…\/~xk - элементарной дизъюнкцией

(все переменные, входящие в ЭК и ЭД попарно различны)

ДНФ от переменных х1…хn называется ф-ла вида K1\/K2\/…\/Km, где Ki, i=1,m – ЭК

КНФ от переменных х1…хn называется ф-ла вида D1\/D2\/…\/Dm, где Di, i=1,m - ЭД

Если в каждую ЭК входят все переменные х1…хn или их отрицания, то такая ДНФ называется совершенной ДНФ.

Т-ма: Любая БФ, отличная от константы 0 (1) мб представлена формулой в виде СДНФ (СКНФ)

Д-во (для первого): рассм некоторую БФ f, отличную от константы 0. Сформируем м-во С1f={~L | f(~L)=1}. Каждый набор из С1f называется конституентой единицы ф-ии f. Т.к. по усл ф-я не равно 0, м-во C1f не пусто. Каждому набору поставим в соответствие ЭК: ~L э C1f -> x1^L1…xn^Ln. Эта формула обращается в единицу только на наборе ~L и равно 0 на любом наборе B, отличном от L.

Тогда искомая ф-ла им вид f=\/x1^L1…xn^Ln, L э C1f.

Полное множество булевых функций. Теорема о доказательстве полноты множества

путем представления его элементов формулами над полным множеством.

М-во БФ наз полным, если любая БФ в нём мб представлена ф-лой над ним.

Т-ма: Пусть F – полн м-во БФ. Если любая функция из F мб представлена формулой над м-вом G, то м-во G также полное.

Д-во: Пусть для люб f э F f(x1…xn)=псиG(x1…xn) (мб предст как)

1. Пусть фи – некот ф-ла над F. Фи=х => y будет формулой и над G.

2. Фи=с э F (пусть фи – некоторая константа из множества F, если она нам существует)

Тогда по предположению существует G.

3. Пусть над м-вом F построена f(Ф1…Фn), где Фi – некоторая ф-ла над F.

Согласно индуктивному предположению над каждой Фi существует эквивалентная ей ф-ла тетаi над множеством G. Тогда f(Ф1…Фn)=f(тета1…тетаn)=псиG. Поскольку в силу полноты любая БФ может быть представлена формулой над F, то эта же БФ мб представлена ф-лой над G.