Теорема Клини

Пусть V=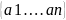 произвольный алфавит. Язык L V*является элементом п\к R(v) он допускается КА.Докажем, что всякий язык из допускается некоторым КА.Для док-ва этого утверждения мы воспользуемся методом индукции по построению языка из R(v) Как элементы замыкания множества 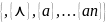.Этот метод состоит следующее сначала утвержденное доказывается для языков исходного множества, а затем в предположении, что утверждение доказано для языков L и K из R(v) оно доказывается для LK,LK,L*.

КА для языков  , ,a

Пусть КА M₁=(V₁,Q₁,q₀₁,F_1,б₁) и M₂=(V₂,Q₂,q₀₂,F_2,б₂)

Входные алфавиты этих автоматов совпадают

Теор. клина для*,.,+.

Докажем теперь, что язык произвольного КА есть элемент п\к ,язык КА, из формулы

Это конечное объединение языков, являющихся определением элементами матрицы стоимостей автомата. Матрица стоимостей есть итерация матрица меток дуг, задающий автомат. Метка каждой дуги- регулярное выражение обозначающее язык из п\к матрица стоимостей является

Итерацией матрицы, все элементы которой могут быть определены Р.В., т.е. . Поэтому в силу теоремы (Если А-матрица, все элементы которой некоторому п\к с интерацией, то все элементы ее интерации А* также этому п\к с интерацией) и матрица стоимостей как будет состоять из языков п\к , что язык КА есть элемент этого п\к.

КА-это анализирующие модели для РЯ. КА не имеет внутр. Памяти, головка движется по ленте только вправо-на 1 ячейку за такт. С ленты можно только читать. Кроме того автомат может переходить « спонтанно» из одного состояния в другое , не читая ленту не продвигая головки-переход состояния про пустой цепочке.

РЯ-R(V) п\к с итерацией состоит из пустого языка, языка всех языков 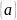,а € V,каждый из которых содержит единственную цепочку а, и замкнутую относительно итерации.

Классы Поста Примеры.Теерема о замкнутости классов Поста.

Пять функциональных классов,называемые классами Поста.

1)Т₀=fP₂:f(0,….0)=0-класс функций, сохраняющих нуль.

2)Т₁= fP₂:f(1,….1)=1 класс функций, сохраняющих 1.

3)L= fP₂:f(x₁,….x_n)=a₀+a₁x₁+a_nx_n-класс линейных функциий,полином жигалкина которых не содержит ни одной коньюкции материалов.

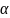4)Класс самодвойственности ф-ий S-fP₂ :f( )= f( )

5)

-класс монотонных функций

Теор.Каждый класс Поста замкнут.

Д-во:Нужно для каждого класса Поста ,доказать что замыкание множества бф С совпадает с С.Пусть f(g_1….g_n)-какая –то суперпозиция над С, обозначим ее через .Без ограничения обязоности можно считать,что все функции f,g_1….g_nP_2n.Рассуждаем,используя индукцию по определению суперпозиции ,если для каждого функция g_ix_i,где x_i-переменное,то =f(x,…x_n)C.предположим,что в суперпозиции все функции g_i есть эл-ты класса Поста C.Докажем, что и =f(g,…g_n)C

1)Если С=Т_0,то

2)При С=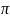 аналогино

3)Пусть с= .Фиксируем произвольно набор Вычислим:

4)С=М.Берем произвольные наборы так,что Докажем М.Имеем: т.к. все функции монотонные и тем сильнее вектор не больше вектора ,а функция f так же монотонна М

.Кольцо.Теорема о тождествах кольца.

Кольцом называют алгебру B=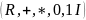 сигнатура которой состоит из 2 бин.опер. и 2 нерванных операций. Равенства для  abcR

1)a+(b+c)=(a+b)+c

2)a+b=b+a

3)a+0=a

4)для каждого aBa’,такой что a+a’=0.

5)a(bc)=(ab)c

6)a1I=1Ia=a

7)a(bc)=ab+ac,(b+c)a=ba+ca связь I и II,согл. Которой операция * дистрибутивна отн. сложения.

Теор. В  кольце выполняются следующие тождества.

1)0a=a0=0

2)(-a)b=-(ab)=a(-b)

3)(a-b)c=ac-dc,c(a-b)=ca=cb

До-во:

1)a+0a=1Ia+0a=(1I+0)a=1Ia=a

2)-(ab)=a(-b)имеем

a(-b)+ab=a((-b)+b)=a0=0

a(-b)=-(ab)

3)a(b-c)=a(b+(-c))=ab+a(-c)=

=ab-ac

.Суперпозиция булевых.Формулы.Процеесс построения формулы и его представление в виде ориентированного дерева.Подформулы.Функция,представляемая формулой.

Пусть бф f есть функция от n переменных,а булев. Функции g₁…g_n-произвольные(и не обяз. Различные) функции от одного и того же числа переменных,которое обозначим m.

Определим ф-ию f(g_1…g_n),названную суперпозицией функций f,g_1….g_nтак ,что для  имеет место равенство:f(g_1…g_n)=

Таким образом ,суперпозиция f(g_1…g_n)есть не что иное, как композиция булевых операторов g₀f,где булев оператор gзадается семейством коорд. функций g_i,i=

Область целостности.Теорема о конечной области целостности.

Областью целостности наз. коммутативное кольцо без делителей нуля.

Теор.Конечная область целостности явл полем.Поле-кольцо, умножение которого коммутативно,а каждый нулевой элемент a имеет обратный элемент относительно умножения т.к. область целостности,по опр. Явл. коммутат. Кольцом,то достаточно доказать,что для конечной области целостности любой ненулевой элемент обратим,т.е. для всякого a0!x,такой что ax=1I.Фиксируем произ. элемент a0 и определяем отображение f_a множества всех ненулевых элементов в себя по формуле f_a(x)=ax(ax0 в области целостности при a0 и x0.Отображение f_a явл. инъекцией поскольку из равенства ax=ay вытекает равенство a(x-y)=0,откуда ввиду отсутствия делителей нуля x-y=0 и x=y т.к. носитель по условию конечен, то согласно теореме(если А-конечное мн-во и f:AA-инъекция,то она явл. сюръекцией и  биекцией),f_a так же и биекция. Поэтому для у!х такой ,что у=ax, в частности ,при y=1 равенство ax=1I вып. для некоторого однозначно определенного x,т.е. x=a^-1

Док-во теормы опирается на условие конечности кольца.Это условие действительно важно.пример кольца умных чисел показывает,что 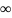область целостности может быть и не полем.