.П/к языков, его замкнутость.

Фор-ка:АлгебраL(V)=(2^V*,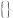,*,, есть замкнутое п/к.Док-во:проверка аксиом п/к сводится к док-ву:1)того,что операция объединения множества всех языков образует коммут и идемпотентный моноид.2)того,что по операции мн-во языков образует моноид. Для этого дост. Доказать,что операция соединения языков ассоциативна ,а так же док-ть для L тож-во : L=L =L,что вытекает из ассоциативности операции соединения слов и из тож-ва х=х=х.3)тождество:

1)Пусть слово х принадлежит его л.ч,т.е. языку L1(L2L3).тогда согласно определению соед. языков ,это слово может быть представленно в виде х=уz,где уL1,иz(L2L3),т.е.zL2zL3.Если zL2,то yzL1L2, а если zL3,то yzL1L3,т.е. х=yzL1L2L1L3.Пусто теперь xL1L2L1L3.Тогда x=yz,где yL,а zL2zL3,т.е. xL1(L2L3)

2)аналогично.

В п/к р=(S,+,*,0,1) отн. порядка вводится следующим образом:для x,yS по определению ху тогда и только тогда ,когда х+у=у т.к. в п/к всех языков в алфавите V операция сложения –это операция объединения мн-в,то в данном случае отношение порядка  есть не что иное,как тоеретико-множ включение .Тогда замкнутость п/к L(V)из  объединения любого семейства множеств служащего точной верхней границы этого семейства,а так же из следующих тождеств:

,что гарантирует выполение непрерывности операции умножения данного п/к,т.е. непрерывности операции соединения эти тождества док-ся,как тождества обычной дистрибутивности. Докажем

Методом двух включений. Если

.Согласно определению объединения семейства множеств, издается такое

Обратное доказываем так из

,что для некоторого

.Неподвижная точка отображения. Теорема о неподвижной точке.

Элемент а множества А называют неподвижной точкой отображения f:А→А, если f(а)=а. Элемент а упорядоченного множества М называют наименьшей неподвижной точкой отображения f:М→М, если он является наименьшим элементом множества всех неподвижных точек отображения f. Теорема о неподвижной точке Формулировка: любое непрерывное отображение f индуктивного упорядоченного множества (М, <) в себя имеет наименьшую неподвижную точку. Доказательство: обозначим через О наименьший элемент множества М. Полагаем f⁰(х)=х и fⁿ(х)= f(f^n-1(х)) для любой n˃0, т.е. fⁿ(х) означает результат n-кратного применения f к х. Рассмотрим последовательность элементов М: {fⁿ(0)}n≥o ={0,f(0), … fⁿ(0) …}. Докажем, что последовательность неубывающая. Используем метод математической индукции. Для элемента О, как наименьшего элемента множества М, имеем 0=f⁰(0)≤f(0). Пусть для некоторых натуральных n верно соотношение f^n-1(0)≤fⁿ(0), согласно теории о «отображении одного индуктивного упорядоченного множества в другом монотонно», отображение f монотонно, и по этому fⁿ(0)=f(f^n-1(0))≤f(fⁿ(0))=fⁿ⁺¹(0),т.е. соотношение верно для номера n+1. Согласно методу математической индукции, fⁿ(0)≤fⁿ⁺¹(0) для любого nEN₀, т.е. последовательность неубывающая. Следовательно, по определению индуктивного упорядоченного множества, она имеет точную верхнюю грань. Обозначим ее через а:а=sup_n≥0fⁿ(0). Докажем теперь, что если у неубывающей последовательности отбросить любое конечное число начальных членов, то ее точная верхняя грань не изменится. Действительно, если а есть точная верхняя грань неубывающей последовательности {х_n}≥0, то а≥х_n для всякого n≥0. В частности фиксируя производную к˃0, для любого n≥к имеем а≥х_n, т.е. а будет верхней гранью подпоследовательности {х_n}n≥k≥0. Докажем, что а является точной верхней гранью этой подпоследовательности. Пусть b какая-то ее верхняя грань, т.е.b≥х_n для любого n≥к. Так как последовательность {x_n}≥0 x_k≤b, то в силу транзитивности отношения порядка x_p≤b и тем самым b≥х_n для любого n≥0, т.е. b есть верхняя грань всей последовательности {x_n}_n≥0. Поскольку а=sup_n≥0x_n, то а≤b и а=sup_n≥k≥0x_n. Следовательно, а – точная верхняя грань подпоследовательности {x_n}_n≥k. В силу непрерывности f получим f(a)=f (sup_n≥0fⁿ(0))=sup_n≥0f(fⁿ(0))=sup_n≥0fⁿ⁺¹(o) но sup fⁿ⁺¹(0)=sup {f¹(0), f²(0) … } = sup_n≥0fⁿ(0)=а

Таким образом, доказано, что а является неподвижной точкой отображения f.Покажем теперь, что найденная неподвижная точка является наименьшей. Пусть для некоторого yEM f(y)=y. Т.к. 0<y, а отображение f, будучи непрерывным, монотонно, то f (0)≤f(y)=y, f(f(0))≤f(f(y))=y и т.д. Следовательно, для любого n≥0, fⁿ(0)≤y, т.е. элемент y есть верхняя грань последовательности {fⁿ(0)} _n≥0. Поскольку а (как точная верхняя грань) есть наименьший элемент на множестве всех верхних граней этой последовательности, то y≥а. Таким образом мы доказали, что произвольная неподвижная точка отображения f не меньше элемента а, т.е. а – наименьшая неподвижная точка отображения f.

Задача о путях во взвешанных графах. Утверждение о вычислении стоимости прохождения по всем путям длины L.Среди задач анализа ор. Графов весьма важны след. Задачи:1)Вычисление для заданного ор, графа его матрицы достижимости. Это задача построения транзитивного замыкания ор. графа. Матрицу достижимости можно рассматривать как матрицу транзитивного и рефлексивного замыкания б.о. непосредственной достижимости в ор. Графе.2)Вычисление таких расстояний между всеми парами вершин в ор. Графе. Это задача о кратчайших расстояниях.3)Перечисление всех путей между двумя произвольными вершинами. Задача о перечисление путей. 3)Метка пути ведущего из вершин v_i в вершину vj , есть произведение в п/к В меток входящих в путь дуг в порядке их следования (для пути ненулевой длины) и есть1I(единица п\к /r ) для пути нулевой длины. Стоимость прохождения из вершин v_i в вершину v_j -это сумма в п\к R меток всех путей, ведущих из вершины v_i в вершину v_j .Лемма. Элемент a^{( e)}_ij матрицы A^e,e0 равен стоимости прохождения из вершины v_i в вершину v_j по всем путям длины L.Док-во: доказательство проведем индукцией по L. При l=e утверждении очевидно, т.к. A=E , Е-единичная матрица, которая матрицей стоимости прохождения по всем путям длины О. l=1: a^{( e)}_ij = a^(e-1)_ik a_ki .Cогласно предложению индукции, элемент a^(e-1)_ik равен стоимости прохождения из вершины v_i в вершину v_j по всем путям длины L-1. Множ. Всех путей длины L из вершины v_i в вершину v_j , проходящих через фиксированную k-ю вершину так, что вер. V_k Связанных с другой вер. V_j Образуется путем присоединения дуги (V_k, V_j) к каждому из путей, ведущих из v_i в v_k и имеющих длину L-1. Тогда видно, что написанное выше выражение для элемента a^{( e)}_ij дает стоимость прохождения из вершины v_i в вершину v_j по всем путям длины L .Т.К. стоимость прохождения между парой вершин v_iv_j равна сумме меток всех путей, ведущих из первой вершины во вторую, а указанную сумму можно получить, 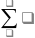послед. Метки путей длины 0,1,2…, то матрица стоимостей взвеш. Ор.графа с учетом леммы может быть представлены в виде:c=A⁰ +A¹+A²…+Aⁿ+=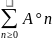 =A*

.Группа.Решение уравнений а*х=b и x*a=bв группе

Группоид G= называют ,если операция ассоциативна, 1I отн. умножения и для каждого хG,такой элемент х’G? называют обращение к х,такой ,что х*х’=x’*x=1I.

Пусть G= -группа a,b- фиксированные элементы G.Рассмотрим задачу решения уравнений

A*x=b x*a=b

В любой группе уравнения вида___ имеют решения,

и притом единственные.

Решение х=а^-1b Решение х=b*a^-1

Действительно, (ba^-1)a=(ba^-1a)=b

A*(a^-1b)=(a*a^-1b)=b До-ем ед. ре-ние

Докажем единстве xa=b-строго

нность решения. a^-1(xa)^a-1=b

Пусть для фиксир В силу ассоциат:

Ованных а и b и x(a^-1a)=a^-1b

Некоторого х вы- x*1I=a^-1b

Полнено равенст x=a^-1b

Во ах=b.В группе Решение ед. в

Для любого а и силу единствен.

однозначно опре обрат. Эл-та.

делен а^-1 обратн

ый к а.Умножив

на него обе части

равенства,получ

има^-1(ах)=а^-1*b.В

силу ассоциатив

ности преобразу

ем последнее к

виду(а^-1*а)*х=а^-1b,

поскольку а^-1*а=1I

то1I*х=а^-1*b,отку

да х=а^-1b.Это реш

ение единс.в силу

единств. обр. эл-та