
- •.Теорема о связи между отношением эквивалентности и разбиением множества.
- •.Критерий полноты системы булевых функций.
- •.Неподвижная точка отображения. Теорема о неподвижной точке.
- •.П/к языков, его замкнутость.
- •.Неподвижная точка отображения. Теорема о неподвижной точке.
- •Теорема Клини
- •Классы Поста Примеры.Теерема о замкнутости классов Поста.
- •Регулярные языки.Индуктивная процедура порождения регулярных языков.Регулярные выражения.Полукольцо регулярных языков.Незамкнутость полукольца регулярных языков.
- •Теорема о регулярности дополнения регулярного языка.Регулярность пересечения,разности и симметрической разности регулярных языков.
- •.Регулярные языки.Индуктивная процедура порождения регулярных языков.Регулярные выражения.Полукольцо регулярных языков.Незамкнутость полукольца регулярных языков.
- •Теорема Лагранжа
- •Конечные автоматы.Представление автомата орг. Графом, взвешанным над п/к регулярных языков.
- •. Дизъюнктивные и конъюктивные нормальные формы. Сднф и скнф. Теорема о представлении булевой функции в виде сднф и скнф.
- •19.1. Базис Жегалкина и его полнота. Полином Жегалкина. Теорема о единственности
- •Полинома Жегалкина для каждой булевой функции
- •Теорема о наименьшем решении линейного уравнения в замкнутом полукольце
- •Классы Поста Примеры.Теерема о замкнутости классов Поста.
- •Область целостности.Теорема о конечной области целостности.
- •.Теорема о связи между отношением эквивалентности и разбиением множества.
.Теорема о связи между отношением эквивалентности и разбиением множества.
Фор-ка:для
любого класса эквивалентости на мн-ве
А множество классов эквивалентности
образует разбиение множества
А.Обратно,любое разбиение мн-ва А задает
на нем отношение эквив совпадают с
эл-ми разбиения.До-во:покажем.что
отношение эквив. Р
на мн-ве определяет некоторое разбиение
этого мн-ва.Убедимся вначале,что любые
2 класса эквив. По отношению р
либо пересек,либо совпад.Пусть 2 класа
эквиви.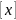 р
и
р
и
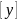 р
имеют общий элемент zpx
,zpy.В
силу симметричности отношения р
имеем xpz,
и тогда xpz
,ypz.В
силу транзитивности отн-ния р
получим
xpy.Пусть
h
р,
тогда hpx
т.к.xpy,то
hpy
h
р.
Обратно,если h
р,то
в силу сим-ти р
получим
hpy,ypx
и в силу транз-ти- hpx,т.е
h
р.
Таким образом
р=
р.Итак,
любые два не совпадающих класса
эквив-ти не пересек. Т.к. для xA
справедливо х
р(поскольку
хрх) ,т.е. каждый элемент мн-ва А
некоторому классу экв-ти по отн. ,
то мно-во
всех классов экв-ти по отношению р
образует разьиение исходного мн-ва
А.Таким образом,любое отношение экв-ти
однозначно определяет некоторое
разбиение.Теперь
р
имеют общий элемент zpx
,zpy.В
силу симметричности отношения р
имеем xpz,
и тогда xpz
,ypz.В
силу транзитивности отн-ния р
получим
xpy.Пусть
h
р,
тогда hpx
т.к.xpy,то
hpy
h
р.
Обратно,если h
р,то
в силу сим-ти р
получим
hpy,ypx
и в силу транз-ти- hpx,т.е
h
р.
Таким образом
р=
р.Итак,
любые два не совпадающих класса
эквив-ти не пересек. Т.к. для xA
справедливо х
р(поскольку
хрх) ,т.е. каждый элемент мн-ва А
некоторому классу экв-ти по отн. ,
то мно-во
всех классов экв-ти по отношению р
образует разьиение исходного мн-ва
А.Таким образом,любое отношение экв-ти
однозначно определяет некоторое
разбиение.Теперь
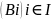 -некоторое
разбиение мн-ва А.Рассмотрим отношение
р,такое
,что xpy
имеет место,когда
хи у
одному и тому же эл-ту
-некоторое
разбиение мн-ва А.Рассмотрим отношение
р,такое
,что xpy
имеет место,когда
хи у
одному и тому же эл-ту
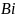 ,данного
разбиения: xpy(iI)
(x
Bi)
(yBi)/.Очевидно,
что введенное отношение рефл. и симм..Если
для х,у,z
имеет место xpy
и ypz,
то x,y,z
в силу отношения p
принадлежат одному и тому же эл-ту Bi
разбиения,хpz
и отношение p
транзитивно.Таким
образом,р- эквив-ть А.Терема позволяет
отождествлять отношения эквивалентности
и разбиения: любая эквивалентность
опр. Единственное разбиение и наоборот.
,данного
разбиения: xpy(iI)
(x
Bi)
(yBi)/.Очевидно,
что введенное отношение рефл. и симм..Если
для х,у,z
имеет место xpy
и ypz,
то x,y,z
в силу отношения p
принадлежат одному и тому же эл-ту Bi
разбиения,хpz
и отношение p
транзитивно.Таким
образом,р- эквив-ть А.Терема позволяет
отождествлять отношения эквивалентности
и разбиения: любая эквивалентность
опр. Единственное разбиение и наоборот.
Транзитивность-БО р на мн-ве А наз. транз-тью,если для х,у,zА из того,что хру и урz xpz.
Симметричность-,если для х,у,zА из xpy урх
Эквивалентность-рефликсивно,сим-но,тран-но.
Рефликсивность-если на мн-ве А содержится в p:idyp,т.е xpx для x
мн-ва А.xA(x,x)p.
Пусть А- произ. мн-во.Сем-во непустых и папарно не пересек. Мн-в назыв разбиением мн-ва А,если объединение мн-в см-ва Bi равно равно АiIВ=А
.Критерий полноты системы булевых функций.
Множество F б ф не содержится ни в одном из классов Поста.
Док-во: необходимость: рассмотрим функцию штрих Шеффера:
Представленное множество бф целиком не принадлежит ни одному из классов Поста.
Если мн-во F целиком какому-либо классу Поста,то в силу замкнутости кл.Поста над мн-вом F не задается получить формулу для I,т.е. мн-во F не будет полным.
Достаточность.
Пусть F-
полное мн-во ,такое что над мн-ом F
можно реализовать
 хотя
бы базис.ь 1)Пусть fF
fI0
,fI1,f(0….0)=1
хотя
бы базис.ь 1)Пусть fF
fI0
,fI1,f(0….0)=1
f(1…1)=0
2)Пусть fF fI0 ,fI1
3)Пусть fF fI0 ,fI1
Итог: Анализируя принадлежность фун-ий мн-ву р первым двум классам, мы можем получить 3 варианта:1)реализовать только отрицание,восп-ся тем,что в мн-ве F есть g,которая не явл самодвойственной и из нее можно получить const 0 и 1.
2)удастся получить 2 конст – и 1 ,восп тем что в мн-ве F есть nM,из нее можно получить отрицание.
3)удастся получить две конст и отрицание.
Таким образом с использованием функции не прик. Четырем классам всегда можно реализовать конст и отрицание.В мно-ве F найдется фун-ция pL,с испл. Конст. И отр из нее всегда можно получить коньюкцию.
Вывод:Если мн-во F целиком не содержится ни в одном из классов Поста,то это множество явл. полным ,т.е. над ним можно реализовать базис
