
- •Теплопередача через плоскую, цилиндрическую (гладкую и оребренную) стенки. Коэффициент теплопередачи. Уравнение теплопередачи.
- •1 Рисунок 19.2 9.2 Теплопередача через цилиндрическую стенку
- •2. Коэффициент теплопередачи.
- •3. Уравнение теплопередачи
- •Тепловая изоляция. Выбор материала тепловой изоляции. Критическая толщина тепловой изоляции труб.
- •3. Критическая толщина тепловой изоляции труб.
- •Основы расчета теплообменных аппаратов. Назначение, классификация и схемы теплообменных аппаратов. Конструктивный и поверочный расчеты теплообменных аппаратов.
- •Гидромеханический расчет теплообменных аппаратов. Технико-экономический расчет.
Теплопередача через плоскую, цилиндрическую (гладкую и оребренную) стенки. Коэффициент теплопередачи. Уравнение теплопередачи.
19.1 Теплопередача через плоскую стенку
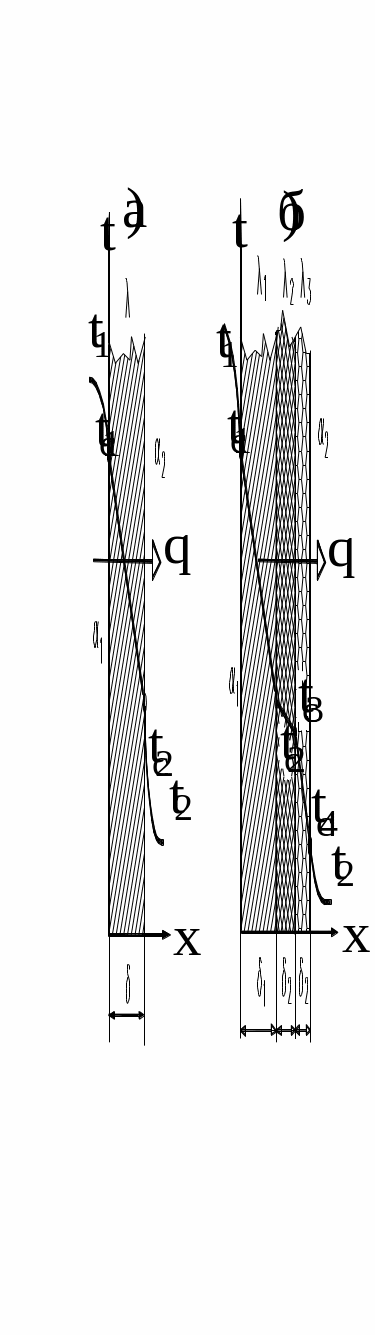
Е
Рисунок 19.1
Плотность теплового потока, передаваемого от горячей среды к стенке, составляет
 ,
(19.1)
,
(19.1)
где
 -
коэффициент теплоотдачи от горячей
среды к стенке,
-
коэффициент теплоотдачи от горячей
среды к стенке,
 - температура горячей среды,
- температура горячей среды,
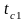 -
температура стенки.
-
температура стенки.
Если стенка не ограничена по высоте и ширине, то в условиях стационарного режима через любую изотермическую поверхность в стенке будет передаваться один и тот же тепловой поток
 ,
(19.2)
,
(19.2)
где
 -
температура стенки со стороны холодной
cреды.
-
температура стенки со стороны холодной
cреды.
При теплоотдаче от стенки к холодной среде плотность теплового потока равна
 ,
(19.3)
,
(19.3)
где
 -
коэффициент теплоотдачи от стенки к
холодной среде,
-
коэффициент теплоотдачи от стенки к
холодной среде,
 -
температура холодной cреды.
-
температура холодной cреды.
При решении уравнений (19.1-19.3) относительно разности температур, получается следующее:
 (19.4)
(19.4)
Сложение левых и правых частей уравнений (19.4) позволяет определить зависимость плотности теплового потока от параметров теплопередачи:
 ,
(19.5)
,
(19.5)
где коэффициент теплопередачи равен
 (19.6)
(19.6)
В случае теплопередачи через n-слойную плоскую стенку (рисунок 19.1,б) коэффициент теплопередачи равен
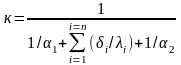 ,
(19.7)
,
(19.7)
где -
толщина и теплопроводность i-го
слоя.
-
толщина и теплопроводность i-го
слоя.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением:
 (19.8)
(19.8)
Температуры на наружных поверхностях стенки определяются по формулам
 (19.9)
(19.9)
Для определения температуры на границе между i-м и (i+1)-м слоями используется формула
 (19.10)
(19.10)
1 Рисунок 19.2 9.2 Теплопередача через цилиндрическую стенку
Особенность теплопередачи через цилиндрическую стенку заключается в том, что поверхности теплообмена снаружи и внутри трубы различны. Исходя из схемы передачи теплоты, представленной на рисунке 19.3,а, можно записать для теплового потока, передаваемого через цилиндрическую стенку, следующие формулы:
Рисунок 19.3
 (19.12)
(19.12)
После решения этих уравнений относительно разности температур и последующего сложения левых и правых частей получается следующее выражение:
 (19.13)
(19.13)
Из (19.13) следует
 (19.14)
(19.14)
Если тепловой поток отнести к 1 метру трубы, то формула (19.14) примет следующий вид
 ,
19.15)
,
19.15)
где
 - линейная
плотность теплового потока,
равная тепловому потоку, передаваемому
через стенку цилиндра длиной 1
м; кl
– линейный
коэффициент
теплопередачи,
равный
- линейная
плотность теплового потока,
равная тепловому потоку, передаваемому
через стенку цилиндра длиной 1
м; кl
– линейный
коэффициент
теплопередачи,
равный
 (19.16)
(19.16)
При теплопередаче через многослойную цилиндрическую стенку линейная плотность теплового потока определяется по формуле
 ,
(19.17)
,
(19.17)
где i - порядковый номер слоя, n - число слоев
19.4 Теплопередача через ребристую стенку

О
Рисунок 19.5
Оребрённая плоская стенка показана на рисунке 19.5,а .
Пусть параметры
гладкой стороны -
 ,
оребренной стороны -
,
оребренной стороны -
 ,
площадь гладкой поверхности - A,
площадь ребристой поверхности -
,
площадь гладкой поверхности - A,
площадь ребристой поверхности -
 ,
теплопроводность стенки -
l
и толщина стенки без учета ребер - d
,
теплопроводность стенки -
l
и толщина стенки без учета ребер - d
В этих условиях процесс теплопередачи описывается уравнениями:
 (19.20)
(19.20)
При решении этой системы уравнений, по ранее применяемой в п.19.1 схеме, получается:
 (19.21)
(19.21)
Если тепловой поток отнести к площади гладкой поверхности, то получается формула для плотности теплового потока
 (19.22)
(19.22)
где
 - коэффициент
оребрения
- коэффициент
оребрения
Для круглой трубы, имеющей наружное оребрение (рисунок 19.5,б), тепловой поток определяется по формуле
 (19.23)
(19.23)
Из-за изменения температуры по высоте рёбер теплоотдача у вершины меньше чем у основания, поэтому для корректировки коэффициента оребрения вводится коэффициент эффективности ребристой поверхности hо , который всегда меньше единицы и определяется по формуле :
 (19.24)
(19.24)
где ηр – коэффициент эффективности ребра, определяемый по специальной методике.
