16. Метод полигонометрии.

Геодезическая сеть — система закрепленных на земной поверхности точек—геодезических пунктов, положение которых определено в общей системе координат.

Геодезические сети строят исходя из общего принципа геодезии — от общего к частному

Полигонометрия – построение геодезической сети путем измерения расстояния и углов между пунктами хода.

Сущность этого метода состоит в следующем. На местности закрепляют систему геодезических пунктов, образующих вытянутый одиночный ход (рис. 14) или систему пересекающихся ходов, образующих сплошную сеть. Между смежными пунктами хода измеряют длины сторон s,-, а на пунктах — углы поворота р. Азимутальное ориентирование полигонометрического хода осуществляют с помощью азимутов, определяемых или заданных, как правило, на конечных пунктах его, измеряя при этом примычные углы у. Иногда прокладывают полигонометрические ходы между пунктами с заданными координатами геодезической сети более высокого класса точности.

Метод полигонометрии в ряде случаев, оказывается более оперативным и более экономичным, чем метод триангуляции. Это обусловлено тем, что в таких условиях на пунктах триангуляции строят более высокие геодезические знаки, чем на пунктах полигонометрии, поскольку в первом случае следует обеспечить прямую видимость между гораздо большим числом пунктов, чем во втором. Постройка ,же геодезических знаков является самым дорогостоящим видом работ при создании геодезической сети (в среднем 50—60 % всех затрат).

Следует отметить также присущие методу полигонометрии недостатки:

-сети полигонометрии, особенно одиночные ходы, являются гораздо менее жесткими геометрическими построениями, чем сети и ряды триангуляции, так как в полигонометрии число геометрических связей между пунктами существенно меньше, чем в триангуляции (при одинаковом числе пунктов в обоих случаях) ;

-число избыточных измерений, а следовательно, и число условных уравнений, в полигонометрии гораздо меньше, чем в триангуляции с таким же числом пунктов, а это значит, что при прочих равных условиях сеть полигонометрии будет менее точной, чем сеть триангуляции;

-контроль полевых измерений в полигонометрии несравненно хуже, чем в триангуляции, так как число условных уравнений в полигонометрии гораздо1 меньше, чем в триангуляции с таким же числом пунктов.

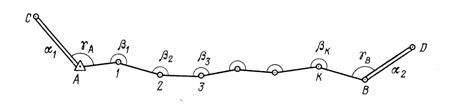
13.Метод триангуляции и его сущность

Геодезическая сеть — система закрепленных на земной поверхности точек—геодезических пунктов, положение которых определено в общей системе координат.

Геодезические сети строят исходя из общего принципа геодезии — от общего к частному

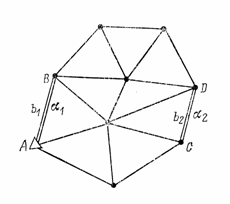
Триангуляция – построение геодезической сети в виде системы треугольников, в которых измерены углы и некоторые стороны, называемые базисными, или просто базисами.

Сущность метода заключается в следующем. На командных высотах местности закрепляют систему геодезических пунктов, образующих сеть треугольников (рис. 13). В этой сети определяют координаты исходного пункта А, измеряют горизонтальные углы в каждом треугольнике, а также длины b и азимуты а базисных сторон, задающих масштаб и ориентировку сети по азимуту.

Сеть триангуляции может быть построена в виде отдельного ряда треугольников, системы рядов треугольников, а также в виде сплошной сети треугольников. Элементами сети триангуляции могут служить не только треугольники, но и более сложные фигуры: геодезические четырехугольники и центральные системы.

Основными достоинствами метода триангуляции являются

-его оперативность и возможность использования в разнообразных физико-географических условиях;

-большое число избыточных измерений в сети, позволяющих непосредственно в поле осуществлять надежный контроль всех измеренных величин;

-высокая точность определения взаимного положения смежных пунктов в сети, особенно сплошной.

Метод триангуляции получил наибольшее распространение при построении государственных геодезических сетей.

В России государственная триангуляция подразделяется на 1, 2, 3 и 4 классы. Триангуляция 1 класса прокладывается по параллелям и меридианам. Ряды переменных между собой образуют системы полигонов. Остающиеся внутри полигонов 1 класса площади заполняются сплошной сетью треугольников 2 класса, сгущаемой затем сетями 3 и4 классов.

1 класс – длина стороны треугольника 20-25 км, 2 класс – 7-20км,

3 класс – 5-8 км,

4 класс – 2-5 км.

В основе метода триангуляции лежит треугольников по стороне и двум углам – теорема синусов.

17. Метод трилатерации и его сущность

Геодезическая сеть — система закрепленных на земной поверхности точек—геодезических пунктов, положение которых определено в общей системе координат.

Геодезические сети строят исходя из общего принципа геодезии — от общего к частному

Трилатерация – построение геодезической сети в виде системы треугольников, в которых измерены все их стороны.

Данный метод, как и метод триангуляции, предусматривает создание на местности геодезических сетей либо в виде цепочки треугольников, геодезических четырехугольников и центральных систем, либо в виде сплошных сетей треугольников, в которых измеряются не углы, а длины сторон. В трилатерации, как и в триангуляции, для ориентирования сетей на местности должны быть определены азимуты ряда сторон.

Метод трилатерации применяют для построения инженерно-геодезических сетей 3 и 4 классов, а также сетей сгущения 1 и 2 разрядов различного назначения.

Сети трилатерации, создаваемые для решения инженерно-геодезических задач, часто строят в виде свободных сетей, состоящих из отдельных типовых фигур: геодезических четырехугольников, центральных систем или их комбинаций с треугольниками.

Типовой фигурой трилатерации является треугольник с измеренными сторонами а, b и с

Метод трилатерации основан на возможности решения треугольника по трем его сторонам a,b,c; углы определяются по теореме косинусов. Так, для угла А имеем

Эту формулу можно привезти к виду

где p – полупериметр, т.е. 2p = a + b + c.

14. способы закрепления пунктов триангуляции