SВопрос №27 (Момент импульса частицы относительно точки, относительно оси)

Д ля отдельно взятой частицы моментом импульса относительно точки O называется псевдовектор M = [rp] = [r(mv)]. Моментом импульса системы относительно точки O называется векторная сумма моментов импульсов частиц, входящих в систему: . Проекция вектора M на некоторую ось z называется моментом импульса частицы относительно этой оси: M_z = [rp]_{пр z}. Моментом импульса системы относительно оси z называется величина . Из рисунка видно, что модуль вектора момента импульса частицы равен M = rpsin = lp, где l=rsin - длина перпендикуляра, опущенного из точки O на прямую, вдоль которой направлен импульс частицы. Эта длина называется плечом импульса относительно точки O. Рисунок выполнен в предположении, что точка O, относительно которой берется момент, и вектор p лежат в плоскости рисунка. Вектор M перпендикулярен плоскости рисунка и направлен «от нас».

Вопрос №28 (Момент силы относительно точки и относительно оси. Пара сил)

П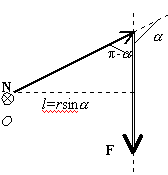 севдовектор N = [rF] называется моментом силы F относительно точки O, из которой проводится радиус-вектор r точки приложения силы. Из рисунка видно, что модуль момента силы можно представить следующим образом: N = rFsin = lF, где l = rsin - плечо силы относительно точки O (т.е. длина перпендикуляра, опущенного из точки O на прямую, вдоль которой действует сила). Проекция вектора N на некоторую ось z, проходящую через точку O, относительно которой определен псевдовектор N, называется моментом силы относительно этой оси: N_z = [rF]_{пр z}. Две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил. Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары. Суммарный момент образующих пару сил F₁ и F₂ равен N = [r₁F₁] + [r₂F₂]. Учтя, что F₁ = -F₂, можно написать: N = -[r₁F₁] + [r₂F₂] = [(r₂ – r₁)F₂] = [r₁₂F₂], где r₁₂ = r₂ – r₁ – вектор, проведенный из точки приложения силы F₁ в точку приложения силы F₂. Выражение не зависит от выбора точки O. Следовательно, момент пары сил относительно любой точки будет один и тот же. Вектор момента пары сил перпендикулярен к плоскости, в которой лежат силы, и численно равен произведению модуля любой из сил на плечо.

Вопрос №29 (Уравнение моментов для системы взаимодействующих частиц)

Силы взаимодействия между частицами действуют в противоположные стороны вдоль одной и той же прямой. Их моменты относительно произвольной точки O равны по модулю и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы частиц, в частности для твердого тела, всегда равна нулю: . В соответствиями с определениями и N = [rF] уравнение можно записать следующим образом: .

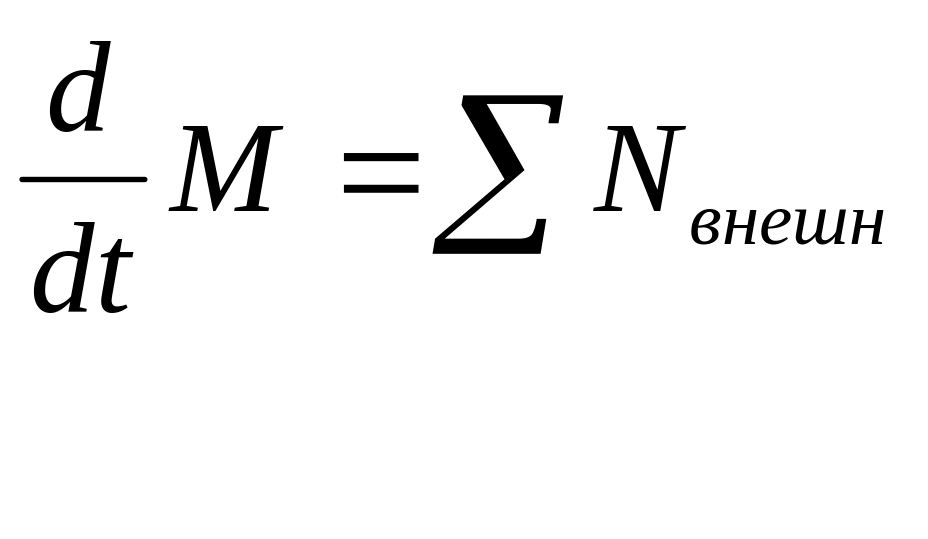Вопрос №30 (Закон сохранения момента импульса системы взаимодействующих частиц)

Из 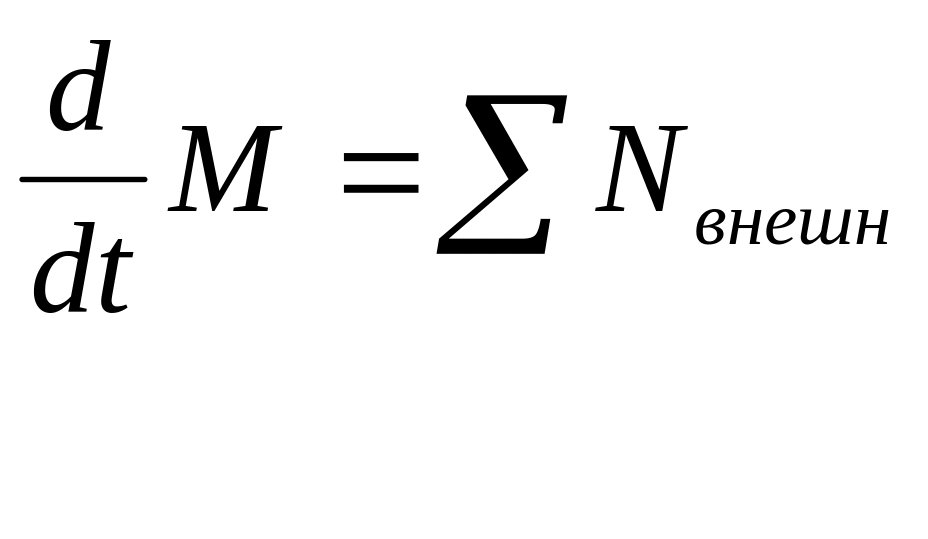вытекает, что при отсутствии внешних сил dM/dt = 0. Следовательно, для замкнутой системы вектор M постоянен. Это утверждение составляет содержание закона сохранения момента импульса, который формулируется следующим образом: момент импульса замкнутой системы материальных точек остается постоянным. Мы доказали соотношение для системы из двух частиц. Однако его легко обобщить на случай любого числа частиц. Напишем уравнения движения частиц: (от 1 до N частиц). Умножив каждое из уравнений на соответствующий радиус-вектор, получим: (от 1 до N частиц). Сложим почленно все N уравнений: . Первая сумма в правой части представляет собой сумму моментов всех внутренних сил, которая, равна нулю ( ). Вторая сумма справа есть сумма моментов внешних сил. Следовательно, мы пришли к формуле . Отметим, что момент импульса остается постоянным и для незамкнутой системы при условии, что суммарный момент внешних сил равен нулю. Спроецировав все величины, входящие в уравнение , на некоторое направление z, получим соотношение , согласно которому производная по времени от момента импульса системы относительно оси z равна сумме моментов внешних сил относительно этой оси. Отсюда же следует, что в том случае, когда сумма внешних сил относительно некоторой оси равна нулю, момент импульса системы относительно этой оси остается постоянным. В заключение отметим, что без указания точки или оси, относительно которых определяется момент, понятия момента импульса и момента силы утрачивают смысл.

Вопрос №31 (Преобразование момента импульса системы частиц при переходе в систему центра масс)

M_O = M_C + [R_C, p], где M_O – момент импульса системы МТ относительно начала O л-системы, M_C – момент импульса относительно центра масс C (собственный момент импульса), R_C – радиус-вектор центра масс в л-системе, p – суммарный импульс системы точек, определенный в л-системе. Воспользуемся соотношениями: R_i = R_C + r_i, V_i = v_C + v_i (см. билет 24). По определению M_O = m_i[R_iV_i] = m_i[(R_C + r_i)(V_C + v_i)] = m_i[R_CV_C] + m_i[R_Cv_i] + m_i[r_iV_C] + m_i[r_iv_i]. Первое слагаемое можно написать в виде [R_C, mV_C] = [R_Cp]. Второе слагаемое [R_C, m_iv_i] = [R_C, mv_C] = 0 (так как V_C – скорость центра масс в ц-системе – есть нуль). Третье слагаемое [m_ir_i, V_C] = [mr_C, V_C] = 0 (потому что r_C – радиус-вектор центра масс в ц-системе – есть нуль). Четвертое слагаемое представляет собой M_C – момент импульса системы МТ в ц-системе. Таким образом, M_O=M_C+[R_C, p], что и требовалось доказать.