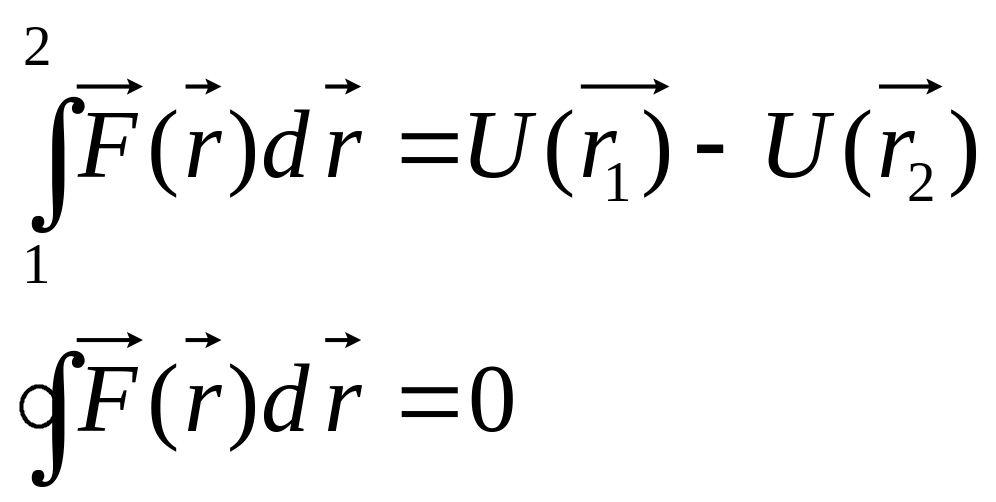- •Вопрос №13(Потенциальная энергия частицы во внешнем поле сил).
- •Вопрос №14(Потенциальная энергия деформированной пружины)
- •Вопрос №15(Потенциальная яма, барьер. Условие равновесия механической системы с одной степенью свободы)
- •Вопрос №18(Потенциальная энергия взаимодействия)
- •Билет №21(Закон сохранения энергии для системы взаимодействующих частиц)
- •Билет №22 (Закон сохранения импульса системы взаимодействующих частиц)
- •Вопрос №25 (Центр масс. Движение центра масс системы частиц)
- •Вопрос №26 (Упругое и неупругое соударение шаров)
- •SВопрос №27 (Момент импульса частицы относительно точки, относительно оси)
- •Вопрос №28 (Момент силы относительно точки и относительно оси. Пара сил)
- •Вопрос №32 (Космические скорости)
- •Вопрос №33 (Силы инерции в поступательно движущейся системе отсчета)
- •Билет №35(Центробежные силы инерции, зависимость ускорения свободного падения от широты местности)
Билеты по физике версия 0.7 beta
Вопрос №1 (Скорость ее компоненты по декартовым координатным осям...)
Средняя
скорость
![]()
Мгновенная
скорость
![]()
![]()
![]()
![]()
![]()
![]()
![]() <V>=S/t
<V>=S/t ![]()
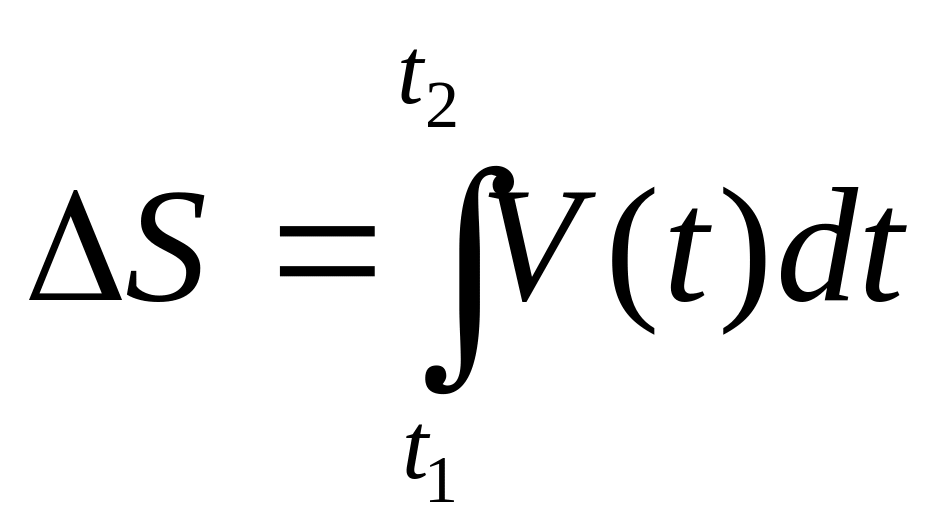 V=
dS/dt dS=Vdt
V=
dS/dt dS=Vdt
![]()
![]()

![]()
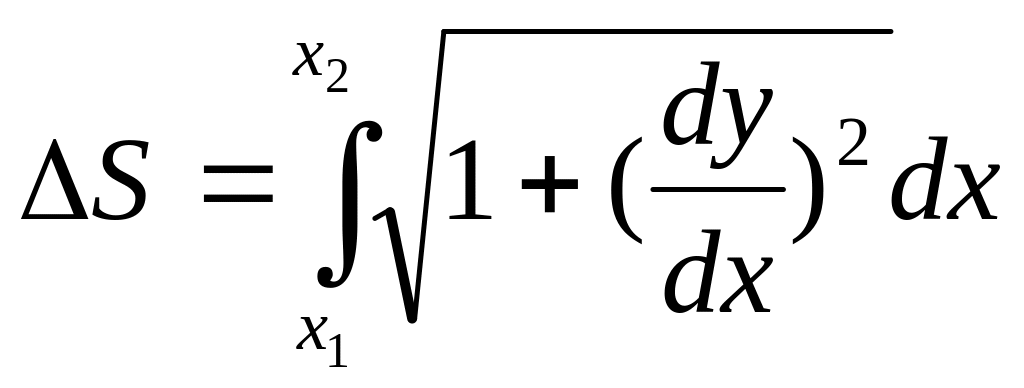
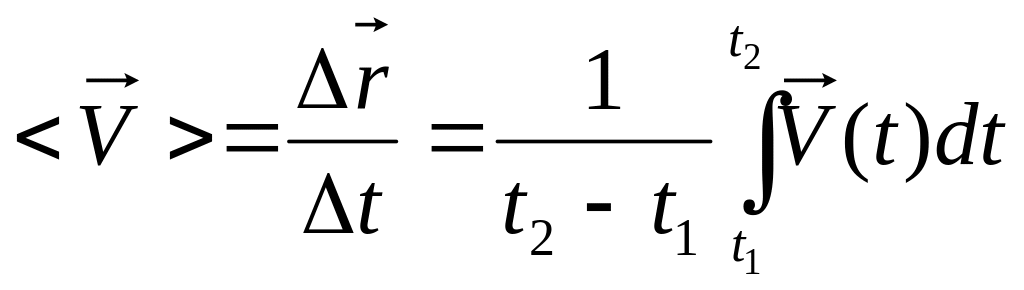
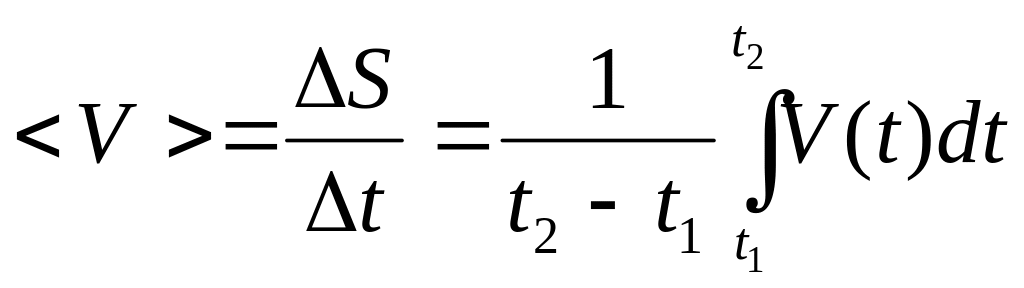
Вопрос №2 (Ускорение, его компоненты по декартовым координатным осям)
Среднее
ускорение
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вопрос №3 (Тангенциальное нормальное и полное ускорение)
![]()
![]()
![]()
![]()
![]()
![]()
![]() C=d/dS-
Кривизна R=dS/d-
радиус кривизны
C=d/dS-
Кривизна R=dS/d-
радиус кривизны
Полное
ускорение
![]()
![]()
Тангенциальное
ускорение
![]()
![]()
Нормальное
ускорение
![]()
Вопрос №4 (Угловая скорость и угловое ускорение. связь между угловыми и линейным…)
Угловая
скорость
![]()
![]()
![]()
Угловое
ускорение
![]()
![]()
![]()
![]()
Вопрос №5 (Принцип относительности Галилея. Преобразования Галилея)
![]()
x=x' +V0t
y=y'
z=z'
![]()
![]()
Принцип относительности:
Все механические явления в различных инерциальных системах отсчета протекают одинаковым образом вследствие чего невозможно никакими механическими опытами установить покоится данная система или движется прямолинейно и равномерно.
Вопрос №6 (Законы Ньютона. Границы применимости классической механики)
1 закон. В инерциальной системе отсчета скорость любого тела остается постоянной пока воздействие на это тело со стороны других тел не вызовет ее изменения
2
закон
![]() или
или
![]()
3
закон
![]()
![]()
Границы применимости :
V<<С
Макротела
Тело- материальная точка
Вопрос №7 (Сила трения. Сухое и жидкое трение)
1) Сухое трение а)Fтрп=F V=0 F<F0
б) Fтрск=kN V>0 F>=F0 {F0=kFn, где k-коэффициент трения }
2) Жидкое трение
Fc={0 если V=0; -k1V если V>0 Re<<1, k1-коэффициент сопротивления; -k2VV Re>>1}
Re=Vl/; Если Re<<1 то течение жидкости ламинарное (при котором соприкасающиеся слои жидкости не перемешиваются, иначе турбулентное течение)
k1 зависит от формы и размеров тела и вязкости жидкости( для шара справедлива формула Стокса k1=6r)
k2 зависит от формы тела и плотности среды.
Вопрос №8 (Сила тяжести и вес)
Вес сила с которой тело действует на подвес или опору вследствие гравитационного притяжения к Земле(G)
Сила
тяжести
![]() Приблизительно
равна силе гравитационного притяжения
к Земле. Различия обусловлены тем, что
система отсчета связанная с Землей не
вполне инерциальная ( различие около
0.36%)
Приблизительно
равна силе гравитационного притяжения
к Земле. Различия обусловлены тем, что
система отсчета связанная с Землей не
вполне инерциальная ( различие около
0.36%)
Вопрос №9 (Закон Кулона Сила Лоренца)
Условия выполнения:
а) Средой является вакуум
б) Точечные заряды
в) V=0
![]()
Принцип
суперпозиция
![]()
![]()
Сила
Лоренца V0
![]()
![]()
![]()
Вопрос №10 (Кинетическая энергия материальной точки и системы материальных точек)
![]()
![]()
![]()
![]()
![]()
T=mV2/2=p2/2m
Аддитивная
величина

Релятивистское
значение
![]()
При V<<C
![]()
Вопрос №11(Теорема о приращении кинетической энергии).
Работа
характеризует приращение энергии,
обусловленное действием силы на
движущуюся частицу. Проинтегрировав
соотношение d(mv2/2)=Fds
вдоль траектории от точки 1 до точки 2
получим:
![]() .
Левая часть представляет собой разность
значений кинетической энергии в точках
2 и 1, т.е. приращение кинетической энергии
на пути 1-2.
.
Левая часть представляет собой разность
значений кинетической энергии в точках
2 и 1, т.е. приращение кинетической энергии
на пути 1-2.
![]() ,
Величина
,
Величина
![]() .
Есть работа силы на пути 1-2(А12).
Работа результирующей всех сил,
действующих на частицу, идет на приращение
кинетической энергии частицы. А12=Т2-Т1.
.
Есть работа силы на пути 1-2(А12).
Работа результирующей всех сил,
действующих на частицу, идет на приращение
кинетической энергии частицы. А12=Т2-Т1.
Вопрос №12(Работа и мощность).
Е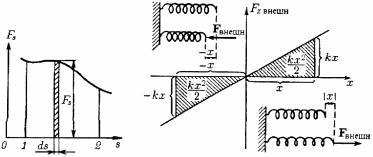 сли
на частицу действует сила F,
то кинетическая энергия не остается
постоянной. В этом случае приращение
кинетической энергии частицы за время
dt
равно скалярному произведению Fds.
Величина
dA=Fds(1)
называется
работой, совершаемой силой F
на пути
ds.
Скалярное произведение (1) можно
представить в виде произведения проекции
силы на направление перемещения FS
и элементарного пути ds.
=>
dA=Fsds.
Из
сказанного ясно, что работа характеризует
изменение энергии, обусловленное
действием силы на движущуюся частицу.
Если сила и направление перемещения
образуют острый угол, то работа >0.
Работа результирующей нескольких сил
равна алгебраической сумме всех работ.
Элементарное перемещение ds
можно представить как vdt.
=>
dA=Fvdt.
Работа,
совершаемая в единицу времени – мощность.
Если за время dt
совершается работа dA,
то мощность равна P=dA/dt.
Или P=Fv.
Поле центральных сил – поле, в котором
направление силы, действующей на частицу
в любой точке пространства, проходит
через неподвижный центр, а модуль силы
зависи только от расстояния до этого
центра F=F(r).Если
во всех точках поля силы, действующие
на частицу, одинаковы по модулю и
направлению, то поле однородное.
сли
на частицу действует сила F,
то кинетическая энергия не остается
постоянной. В этом случае приращение
кинетической энергии частицы за время
dt
равно скалярному произведению Fds.
Величина
dA=Fds(1)
называется
работой, совершаемой силой F
на пути
ds.
Скалярное произведение (1) можно
представить в виде произведения проекции
силы на направление перемещения FS
и элементарного пути ds.
=>
dA=Fsds.
Из
сказанного ясно, что работа характеризует
изменение энергии, обусловленное
действием силы на движущуюся частицу.
Если сила и направление перемещения
образуют острый угол, то работа >0.
Работа результирующей нескольких сил
равна алгебраической сумме всех работ.
Элементарное перемещение ds
можно представить как vdt.
=>
dA=Fvdt.
Работа,
совершаемая в единицу времени – мощность.
Если за время dt
совершается работа dA,
то мощность равна P=dA/dt.
Или P=Fv.
Поле центральных сил – поле, в котором
направление силы, действующей на частицу
в любой точке пространства, проходит
через неподвижный центр, а модуль силы
зависи только от расстояния до этого
центра F=F(r).Если
во всех точках поля силы, действующие
на частицу, одинаковы по модулю и
направлению, то поле однородное.
Вопрос №13(Потенциальная энергия частицы во внешнем поле сил).
Потенциальная энергия – работа, которую совершают консервативные силы при перемещении м.т из точки 1 в точку где п.э. условно принята равной 0. Консервативные силы – силы, работа которых не зависит от пути. В случае, когда работа сил поля не зависит от пути, а зависит лишь от начального и конечного положений частицы, каждой точке поля можно сопоставить некоторую функцию U(x,y,z) такую, что разность значений этой функции в точках 1 и 2 будет определять работу сил при переходе частицы из первой точки во вторую. A12=U1-U2. Это сопоставление можно осуществить следующим образом. Некоторой исходной точке О припишем произвольное значение функции, равное U0. Любой другой точке Р припишем значение U(P)=U0+APO, где APO – работа, совершаемая над частицей консервативными силами при перемещении частицы из точки P в точку О. Поскольку работа не зависит от пути, то U(P) – однозначно(В.В.Жириновский).U1-U2=A10-A20=A10+A02. =>A12=U1-U2. T2-T1=U1-U2=> T2+U2=T1+U1=>E=U+T.=>U входит слагаемым в интеграл движения, имеющий размерность энергии. В связи с этим функцию U(x,y,z) называют потенциальной энергией частицы во внешнем поле сил. Величину Е – полной механической энергией частицы.
Вопрос №14(Потенциальная энергия деформированной пружины)
Потенциальной энергией могут обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело. В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела(например, от расстояния между соседними витками). Как на сжатие так и на растяжение пружины на x необходимо затратить работу A=kx2/2. Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения имеет вид U= kx2/2, где k- жесткость пружины. Эта формула написана в предположении, что потенциальная энергия недеформированной пружины равна 0.
Вопрос №15(Потенциальная яма, барьер. Условие равновесия механической системы с одной степенью свободы)
Р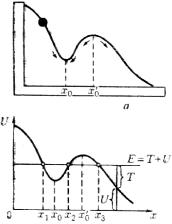 ассмотрим
материальную точку, движение которой
ограничено таким образом, что она имеет
лишь одну степень свободы.(одна независимая
величина с помощью которой можно задать
положение системы).Это означает, что её
положение может быть определено с
помощью одной величины, например
координаты x.
В качестве примера можно привести шарик,
скользящий без трения по укрепленной
неподвижно, изогнутой в вертикальной
плоскости проволоке. На шарик действует
сила тяжести. Сила с которой проволока
действует на шарик всегда перпендикулярна
к скорости шарика и работы над шариком
не совершает => E=T+U=const.
=>Кинетическая энергия может возрастать,
только из-за уменьшения потенциальной.
=> Если скорость шарика=0, а потенциальная
энергия имеет минимальное значение, то
без воздействия из вне не он сможет
придти в движение…Зная вид функции,
которой выражается потенциальная
энергия, можно сделать ряд заключений
о характере движения частицы. Поясним
это, воспользовавшись графиком,
изображенным на рис. Если полная энергия
имеет значение, указанное на рисунке,
то частица может совершать движение
либо в пределах
от
x1
до
x2,
либо
в пределах от x3
до бесконечности. В области x2<x<x3
частица проникнуть не может, так как
потенциальная энергия не может стать
больше полной энергии. Таким образом,
область x2<x<x3
представляет собой потенциальный
барьер,
через который частица не может проникнуть,
имея данный запас полной энергии. Область
x1<x<x2
– потенциальная
яма.
ассмотрим
материальную точку, движение которой
ограничено таким образом, что она имеет
лишь одну степень свободы.(одна независимая
величина с помощью которой можно задать
положение системы).Это означает, что её
положение может быть определено с
помощью одной величины, например
координаты x.
В качестве примера можно привести шарик,
скользящий без трения по укрепленной
неподвижно, изогнутой в вертикальной
плоскости проволоке. На шарик действует
сила тяжести. Сила с которой проволока
действует на шарик всегда перпендикулярна
к скорости шарика и работы над шариком
не совершает => E=T+U=const.
=>Кинетическая энергия может возрастать,
только из-за уменьшения потенциальной.
=> Если скорость шарика=0, а потенциальная
энергия имеет минимальное значение, то
без воздействия из вне не он сможет
придти в движение…Зная вид функции,
которой выражается потенциальная
энергия, можно сделать ряд заключений
о характере движения частицы. Поясним
это, воспользовавшись графиком,
изображенным на рис. Если полная энергия
имеет значение, указанное на рисунке,
то частица может совершать движение
либо в пределах
от
x1
до
x2,
либо
в пределах от x3
до бесконечности. В области x2<x<x3
частица проникнуть не может, так как
потенциальная энергия не может стать
больше полной энергии. Таким образом,
область x2<x<x3
представляет собой потенциальный
барьер,
через который частица не может проникнуть,
имея данный запас полной энергии. Область
x1<x<x2
– потенциальная
яма.
Вопрос №16 (Закон сохранения энергии частицы движущейся в консервативном поле сил)
Поле остающееся постоянным во времени называется стационарным. Поле консервативных сил -стационарное поле, для которого работа совершаемая над частицей силами поля зависит лишь от начального и конечного положений частицы и не зависит от пути по которому двигалась частица.
![]() d(T+U)=0 E=T+U-
полная мех энергия частицы dE=0
=> Е=const;
d(T+U)=0 E=T+U-
полная мех энергия частицы dE=0
=> Е=const;
Интеграл
движения-
![]()
Вопрос №17 (Связь между потенциальной энергией и силой)

Fxdx+Fydy+Fzdz=-dU=-(U((x+dx),(y+dy),(z+dz))-U(x,y,z))
![]()
![]()
![]()
![]()
![]()
U(x,y,z)=U
![]()
Градиент скалярной функции -вектор направленный вдоль направления наибыстрейшего возрастания скалярной функции и равный по модулю производной по этому направлению.
Полный дифференциал функции F(x,y,z) называется приращение, которое получает эта функция при переходе от точки с координатами x,y,z в соседнюю точку с координатами x+dx, y+dy, z+dz. По определению это приращение равно df(x,y,z)=f(x+dx,y+dy,z+dz)-f(x,y,z)
Полное приращение функции при переходе из начальной точки в конечную равно
![]()
Выводы