Как найти пересечение луча, по направлению заданного вектора и треугольника?
Определить пересекается ли вектор с плоскостью треугольника. Найти координаты точки пересечения плоскости и вектора. Строим прямые, проходящие через стороны треугольника и проверяем полученные координаты пересечения на попадание в тр-к.
Как можно задать матрицу расположения модели объекта сцены с учетом расположения «камеры»?
Задание 3D объекта и его создание разбивается на несколько этапов, в процессе которых последовательно преобразуется система координат. Изначально объект задается в некоторой своей локальной системе координат, которая затем размещается в мировой системе координат. Далее определяем видовую систему координат, задавая картинную плоскость, положение глаза (камеры) и систему координат камеры.
Основной задачей проектирования является перевод 3-х мерного объекта, заданного в видовой системе координат, в 2-х мерный объект нормализованной системы координат устройства.
При проектировании отсекаются объекты, которые не попадают в область видимости, а также определяется множество значений z (zI[near; -far]), для которого точки, имеющие значения координаты z, принадлежащие этому множеству, являются видимыми, а точки, находящиеся слишком близко ( ) или слишком далеко ( ) – невидимыми.
Преобразования над объектами по функциональному признаку можно разделить на следующие группы:
моделирующие преобразования (аффинные преобразования); видовые преобразования (положение, направление камеры и т.д.); задание проекции; задание области видимости.
Моделирующие преобразования определяют положение объекта в мировом пространстве. Изначально матрица видового преобразования строится на основе информации о параметрах камеры (положении направлении камеры, положительного направления) и положении мира относительно камеры.
Матрица расположения камеры задается между матрицей Мира (размещение всех объектов) и матрицей перспективной проекции («взгляд» на объекты).
Интерполяция (определение, для каких целей используется в кг)
Достаточно типичной является следующая задача: по заданному массиву точек на плоскости (2D) или в пространстве (3D) построить кривую либо проходящую через все эти точки (задача интерполяции), либо проходящую вблизи от этих точек (задача сглаживания).
Интерполя́ция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Линейная интерполяция. Она состоит в том, что заданные точки М(xi, yi) (i = 0, 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается к ломаной с вершинами в данных точках. Уравнения каждого отрезка ломаной линии в общем случае разные. Поскольку имеется n интервалов (xi , xi + 1), то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности, для i - го интервала можно написать уравнение прямой, проходящей через точки (xi , yi) и (xi + 1, yi + 1), в виде:
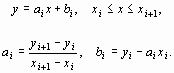
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (см. выше) и найти приближенное значение функций в этой точке.
Квадратичная интерполяция. В случае квадратичной интерполяции в качестве интерполяционной функции на отрезке (xi - 1,xi + 1) принимается квадратный трехчлен.
Уравнения квадратного трехчлена: y = aix2 + bix + ci,, xi – 1<=x <= xi + 1, содержат три неизвестных коэффициента ai, bi, ci, для определения которых необходимы три уравнения.. Ими служат условия прохождения параболы через три точки (xi - 1, yi - 1), (xi, yi), (xi + 1, yi + 1).
Эти условия можно записать в виде:
ai (xi-1)^2 + bi (xi – 1) + ci = (yi – 1),
ai xi^2 + bi xi + ci = yi,
ai (xi+1)^2 + bi (xi + 1) + ci = (yi + 1).
Интерполяция для любой точки x принадлежащей [x0, xn] проводится по трем ближайшим точкам.
Цели. (КГ)
В случае с изображением мы имеем дело не просто с функцией, заданной в отдельных точках. Эти точки имеют «область влияния» — пикселы с ненулевой площадью. И, говоря об увеличении или уменьшении разрешения, мы не должны при этом менять площадь всего изображения. Если обратиться к рисунку, то это правило выглядит так:
+-----------+-----------+-----------+-----------+
| X-----|-----X-----|-----X-----|-----X |
+-----------+-----------+-----------+-----------+
A B C D
+-----+-----+-----+-----+-----+-----+-----+-----+
| X--|--X--|--X--|--X--|--X--|--X--|--X--|--X |
+-----+-----+-----+-----+-----+-----+-----+-----+
a b c d e f g h
Требование сохранения площади (границ области, покрываемой пикселами) дает совсем другое расположение центров пикселов, в которых производятся вычисления.
Улучшение качества текстурирования. Анимация.
Вычисление траекторий, задание цветов, для представления координат не точных, а примерных.