
Theme 1. Matrices and determinants
Calculate a determinant
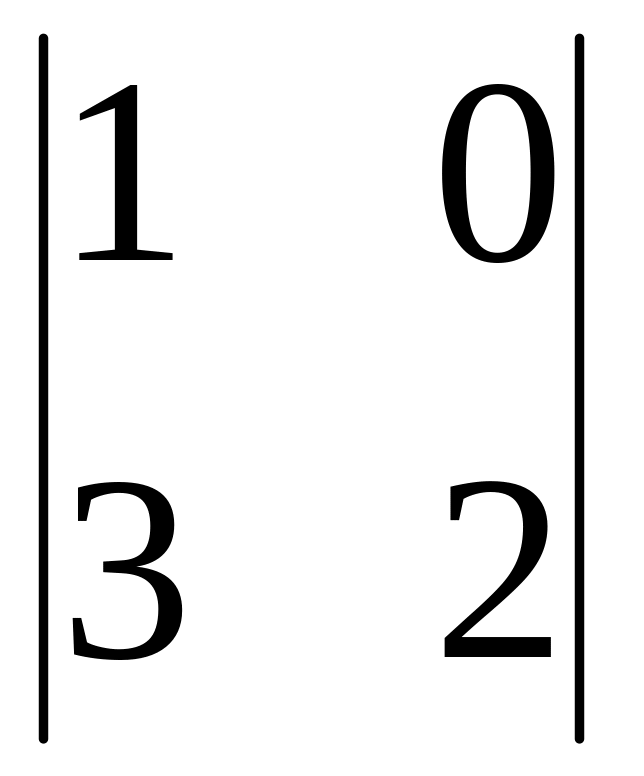 .
.
Calculate a minor
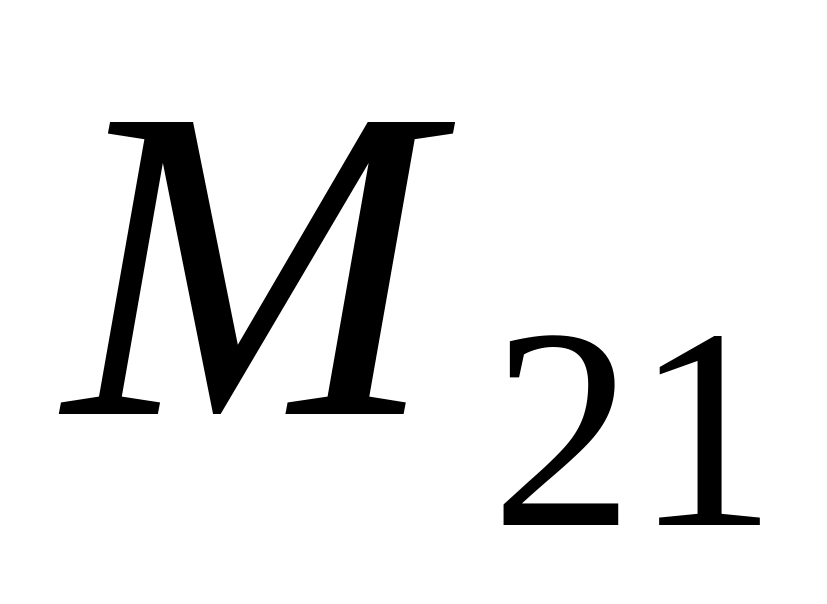 of
an element
of
an element
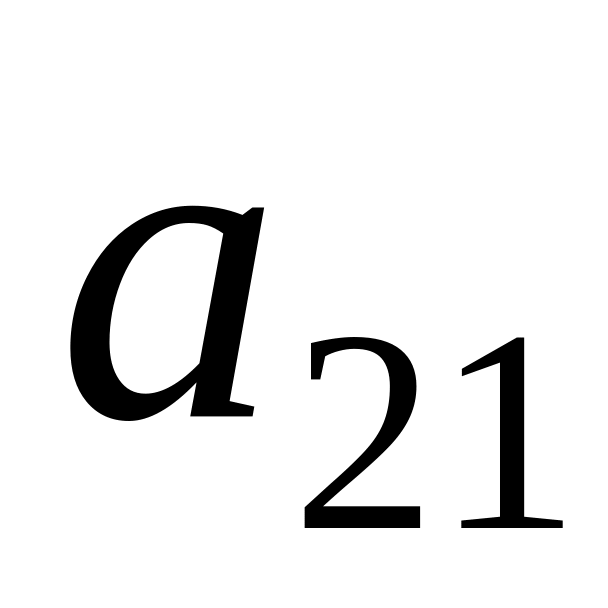 of
a matrix
of
a matrix
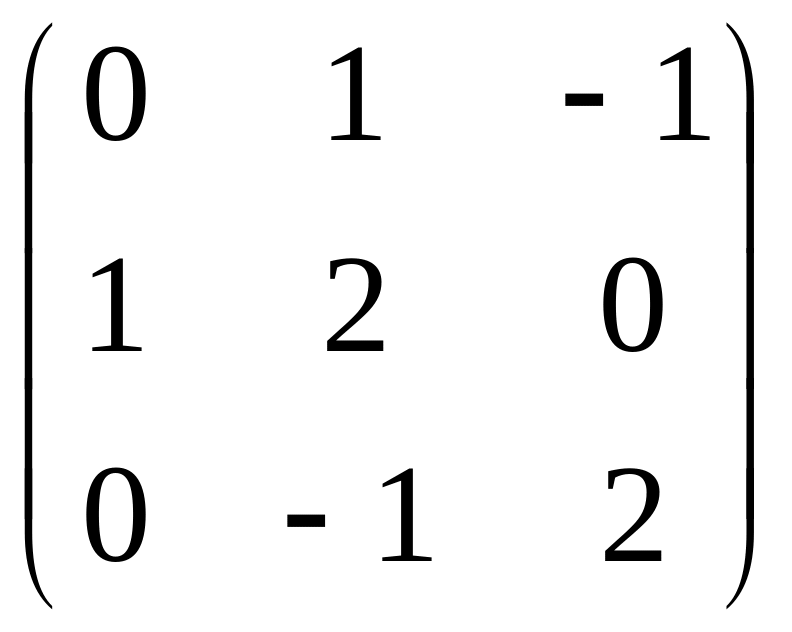 .
.
Calculate a determinant .
Find a matrix
 ,
if
,
if
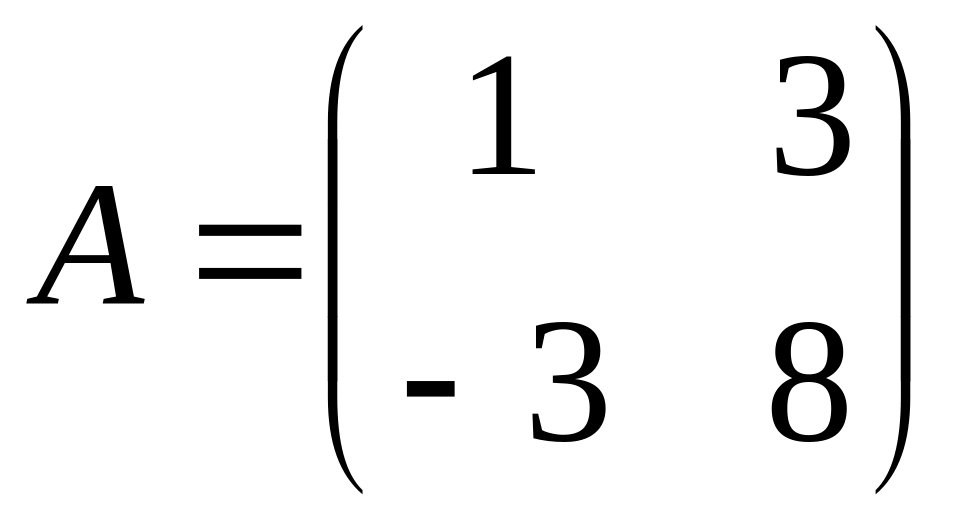 .
.Calculate product of matrices
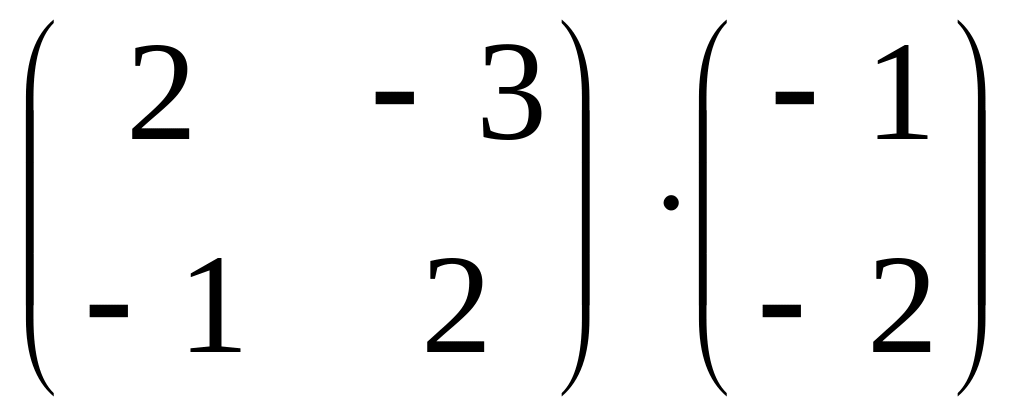 .
.Find an inverse matrix
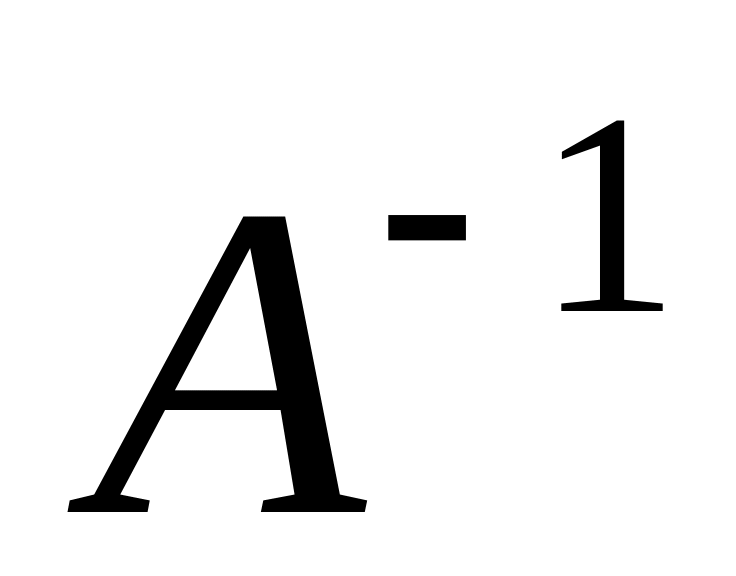 ,
if a matrix
,
if a matrix
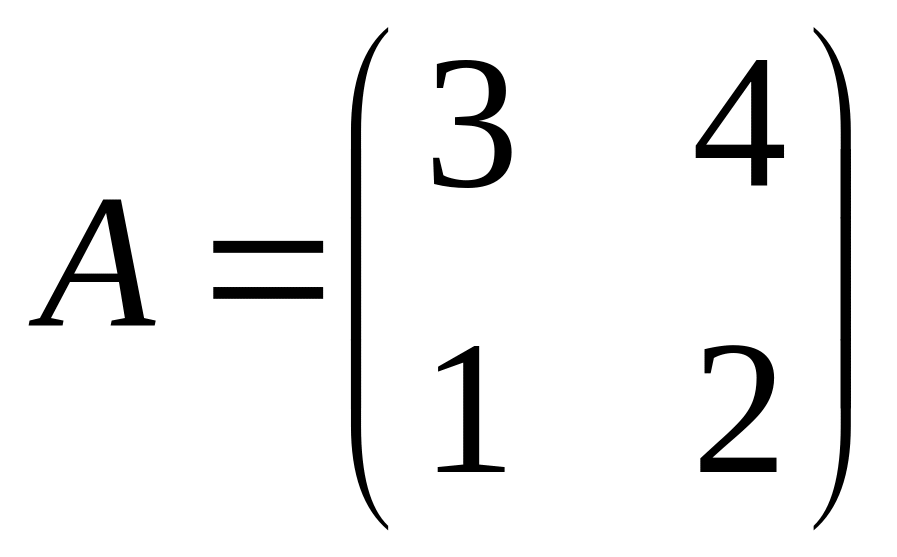 .
.Calculate a determinant .
Matrices
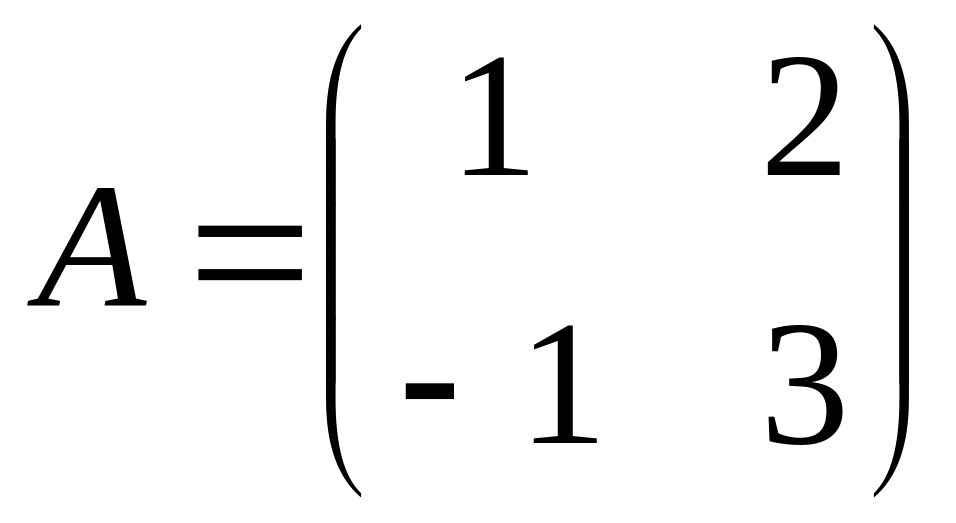 and
and
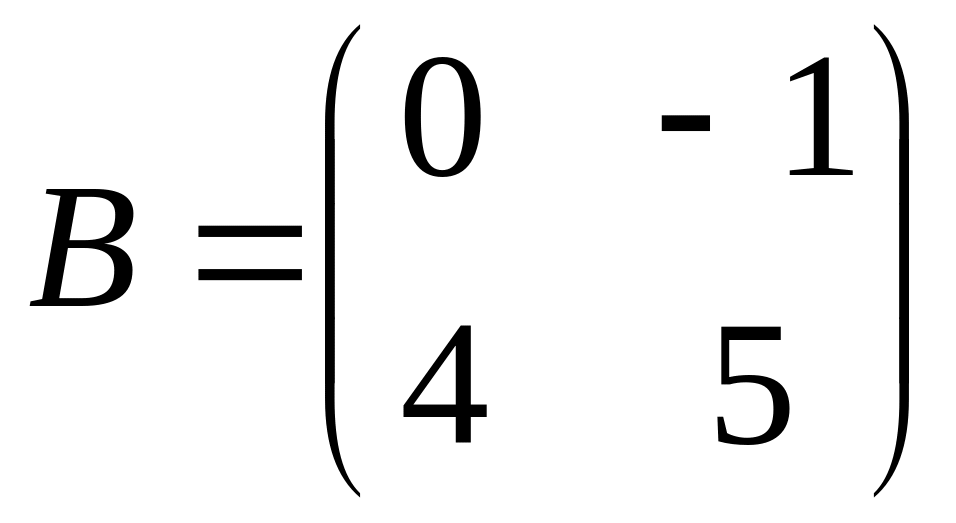 are given. Find product of matrices
are given. Find product of matrices
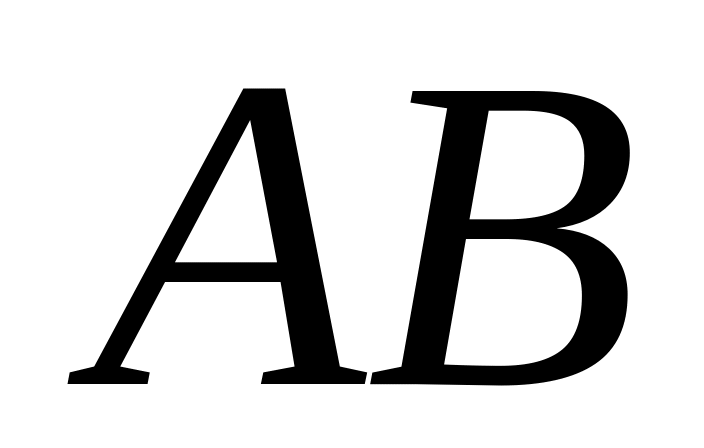 .
.
Matrices and are given. Find the sum of matrices
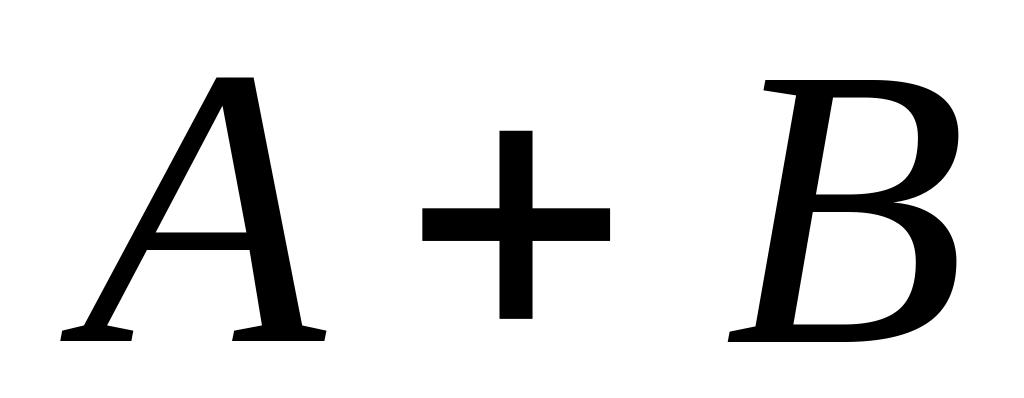 .
.
Find a matrix
 ,
if a matrix
,
if a matrix
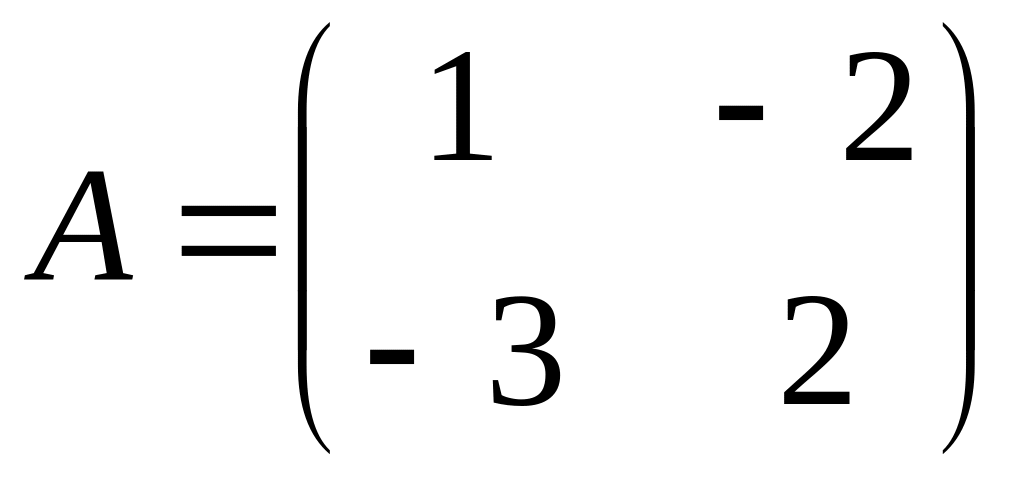 .
.Find a matrix , if a matrix .
Determinant of a matrix
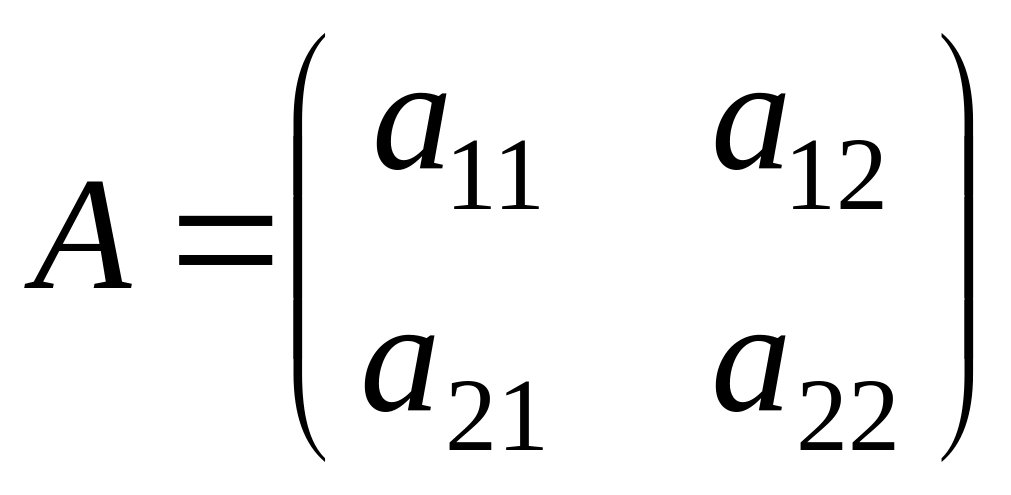 is the number, equal to:
is the number, equal to:At transposing of a square matrix its determinant:
If elements of two lines are proportional, a determinant:
Solve the matrix equation
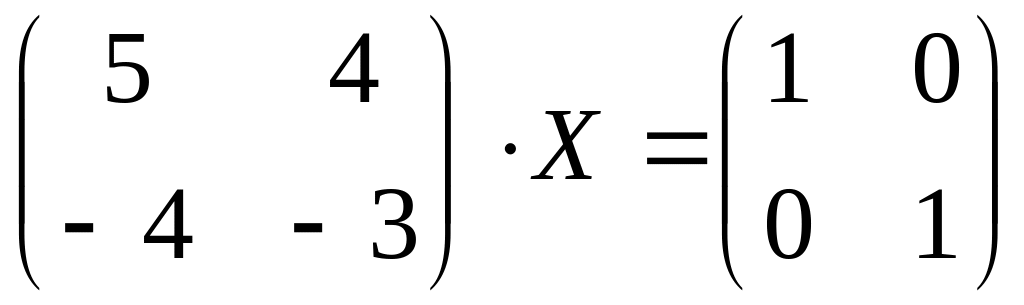 .
.Find product of matrices
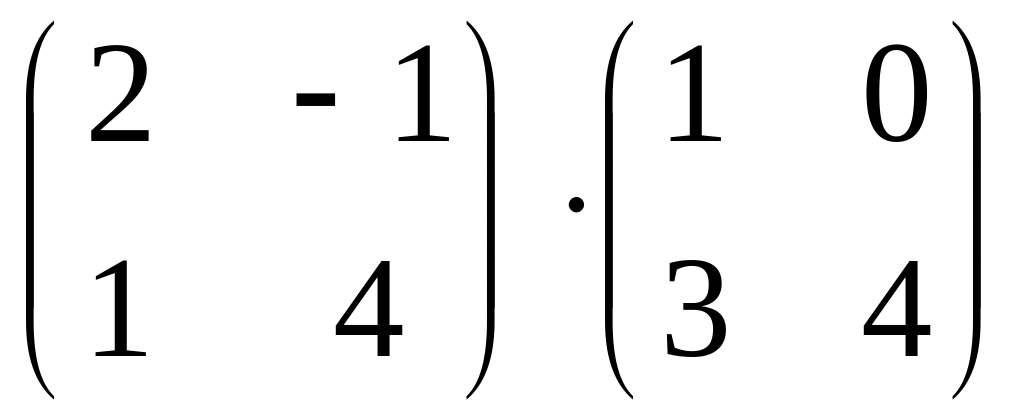 .
.Find
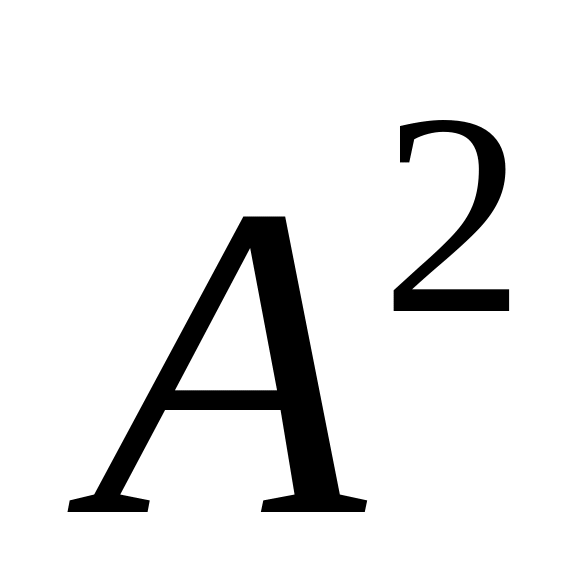 ,
if a matrix
,
if a matrix
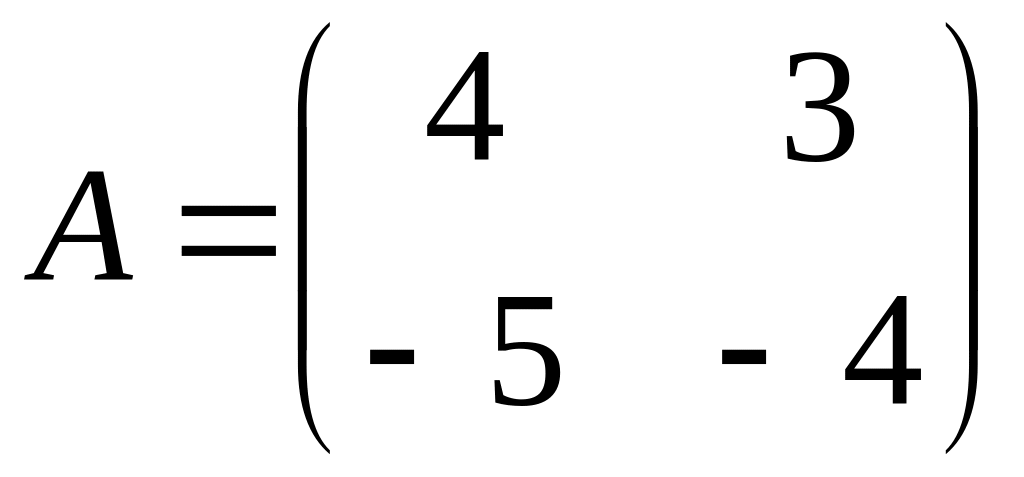 .
.Determinant of the third order
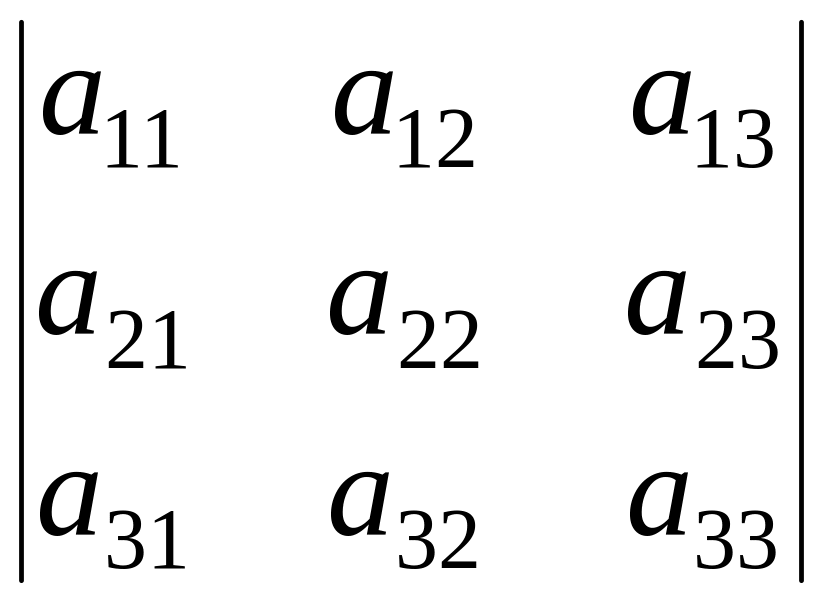 is equal:
is equal:Calculate product of matrices , if
 and
and
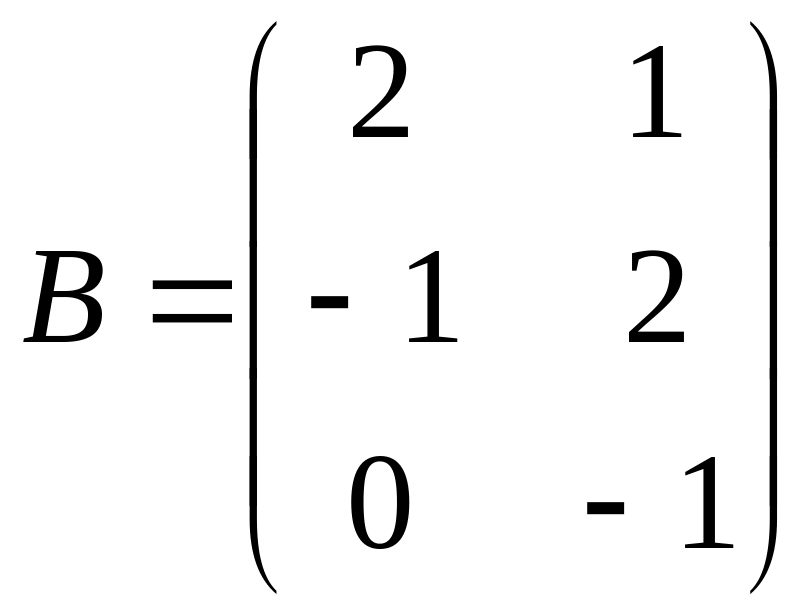 are given.
are given.If
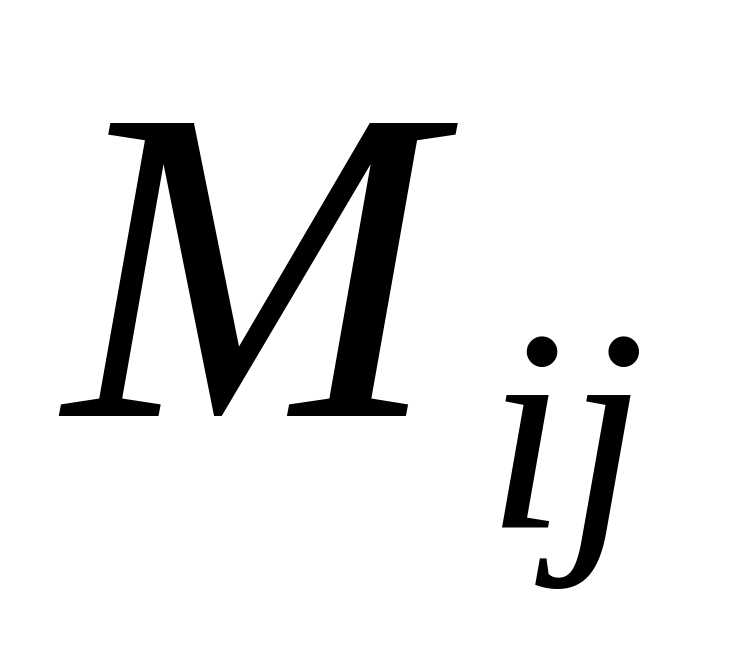 -
a minor of a determinant of an element
-
a minor of a determinant of an element
 ,
then algebraic complement of this element
,
then algebraic complement of this element
 is
equal:
is
equal:If in a determinant to change places of a lines, then:
If any line in a determinant to add with other line:
If in a determinant two columns are proportional, then:
To what value the determinant of an unitary matrix is equal?
Matrix
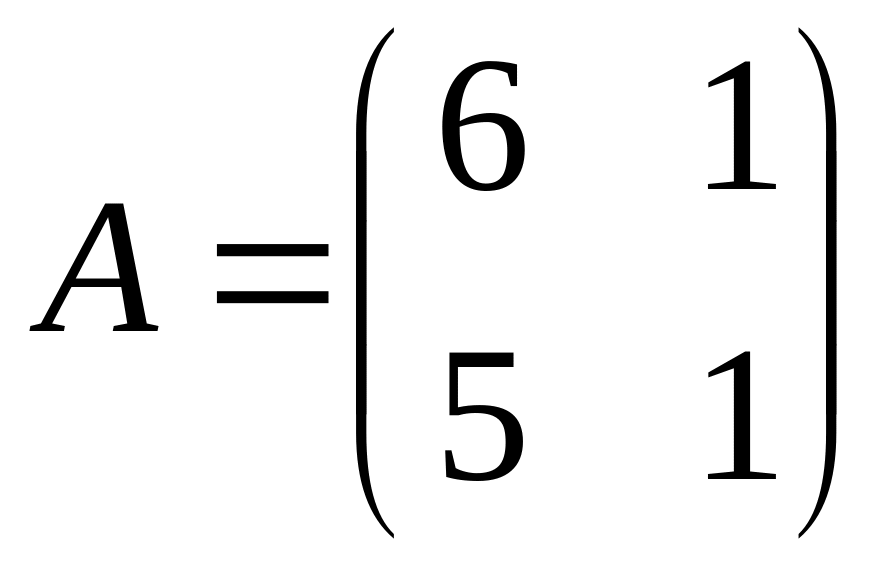 is given. Find an inverse matrix
.
is given. Find an inverse matrix
.Calculate a determinant
 .
.Calculate a minor
 of a determinant
of a determinant
 .
.Calculate a determinant
 .
.Calculate algebraic complement
 of a determinant
of a determinant
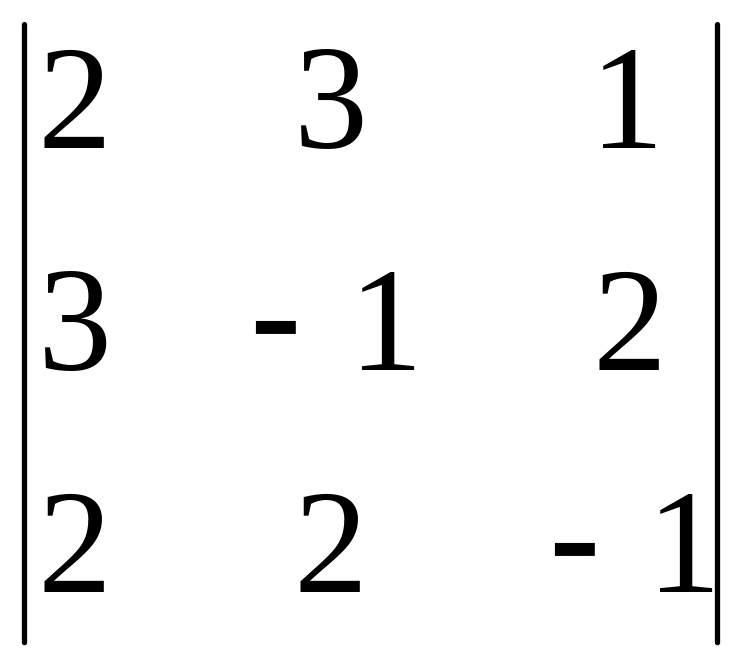 .
.Find product of matrices
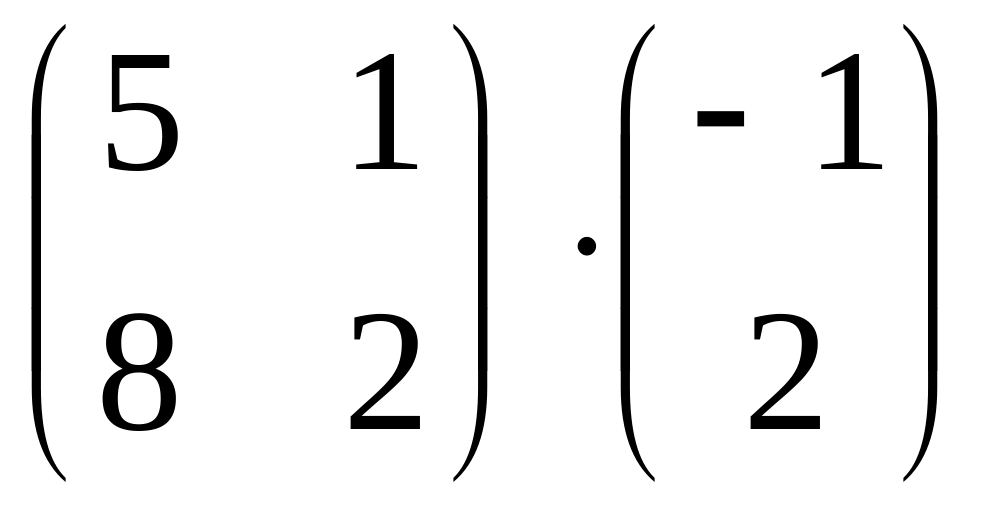 .
.Find an inverse matrix , if
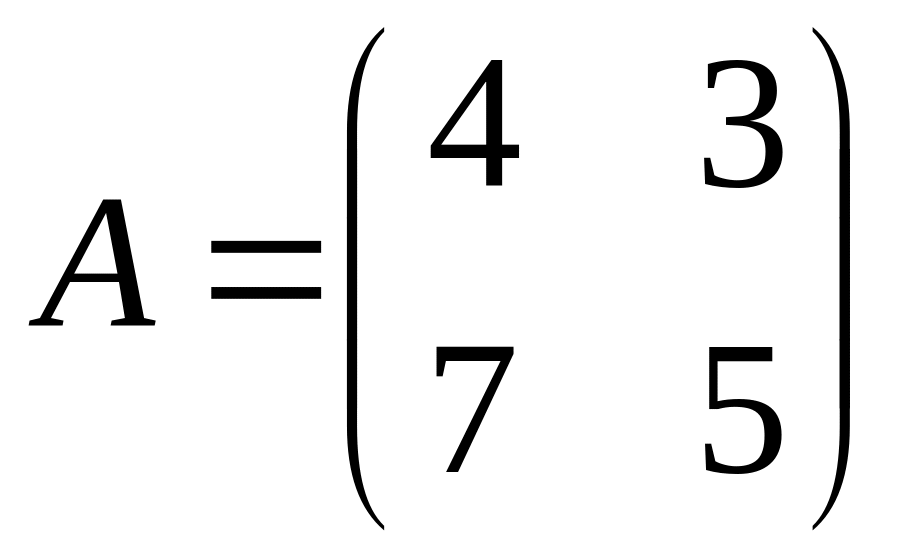 .
.Find an inverse matrix , if
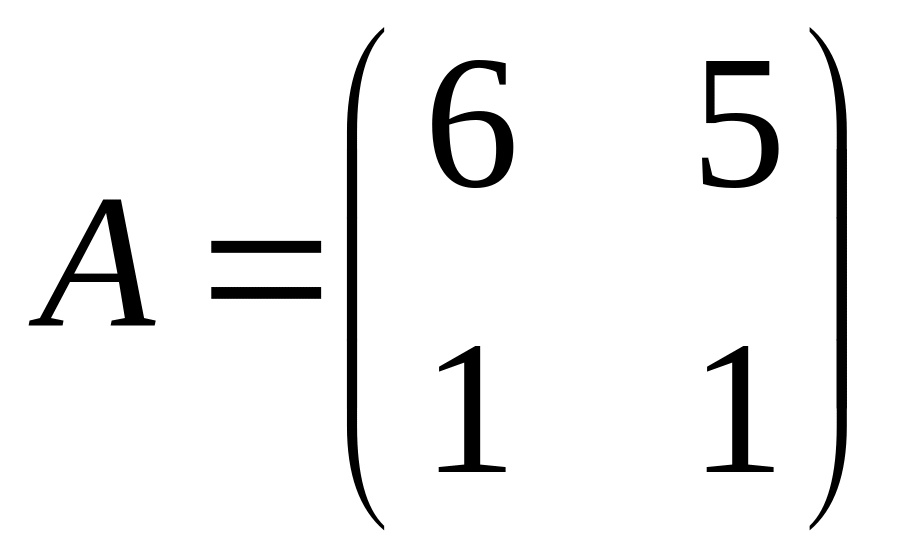 .
.Find a matrix
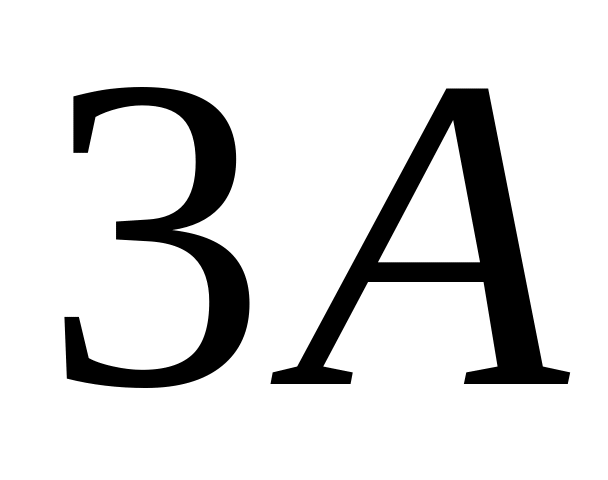 ,
if a matrix
,
if a matrix
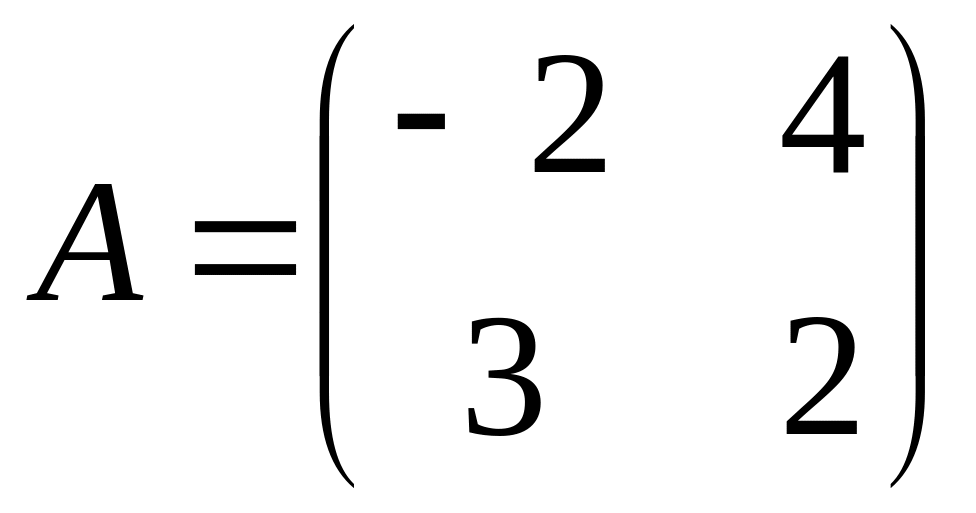 .
.Calculate product of matrices
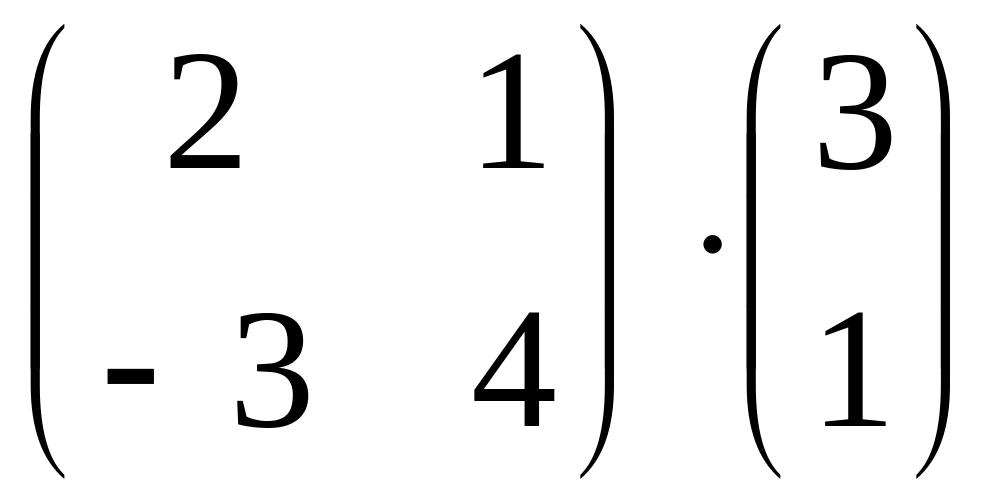 .
.Find an inverse matrix , if
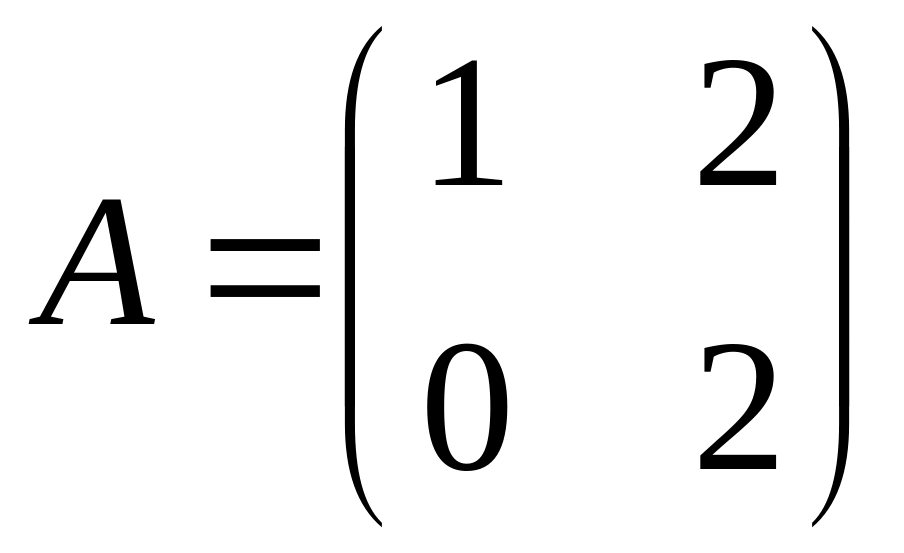 .
.Matrix
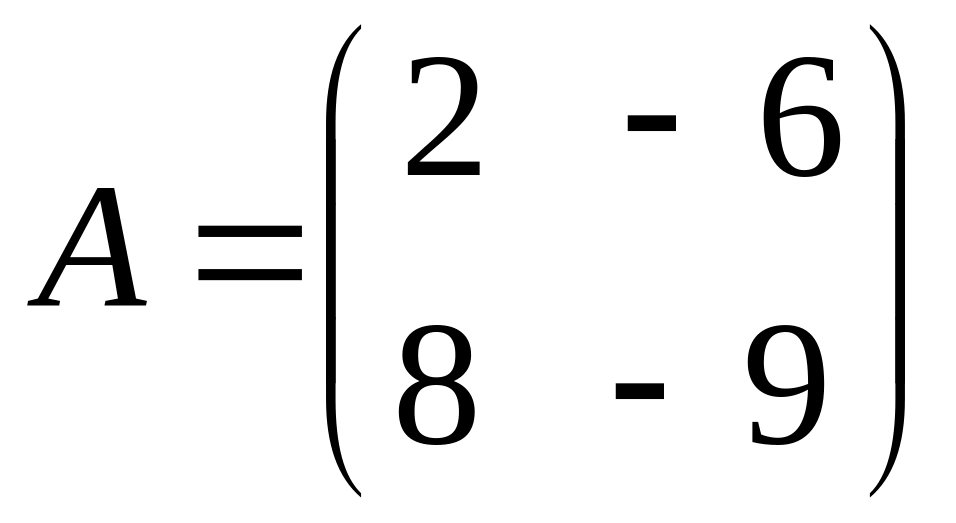 is given. Find the transposed matrix
is given. Find the transposed matrix
 .
.Calculate a determinant
 .
.Calculate a determinant
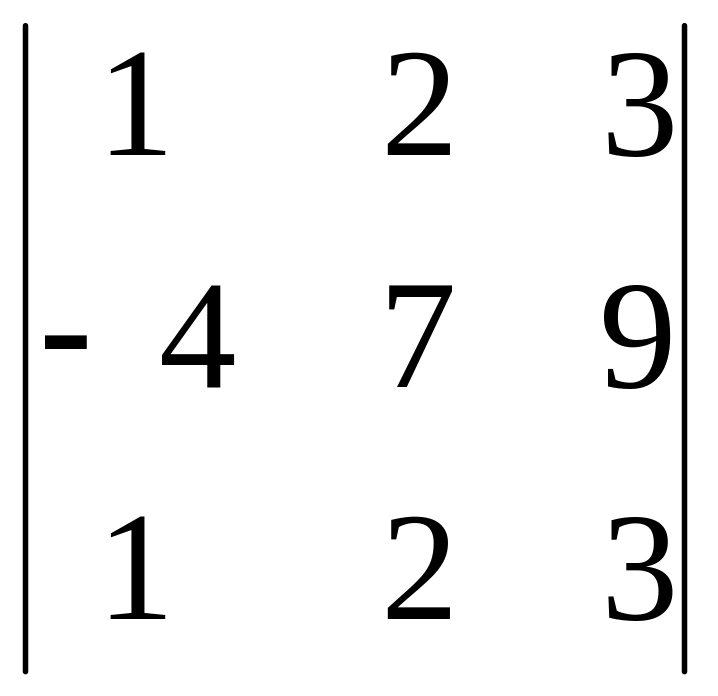 .
.Сalculate a minor
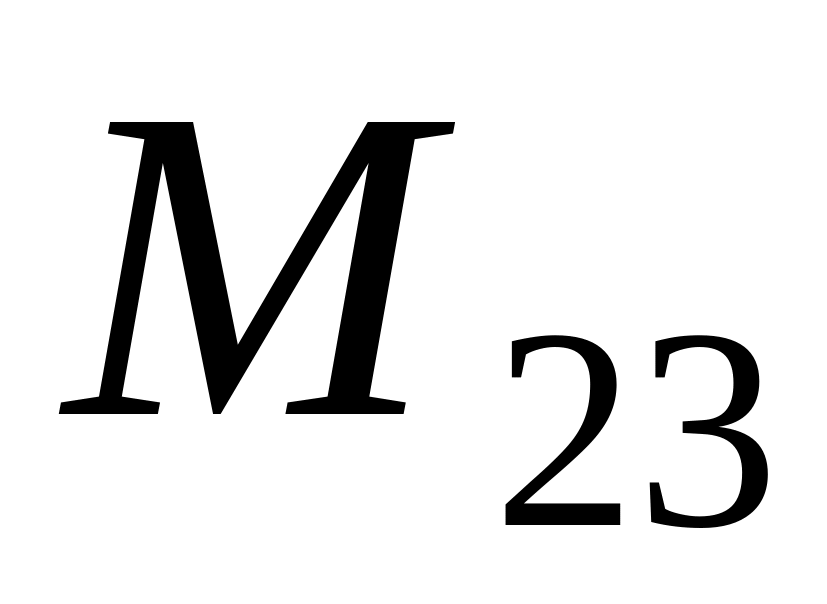 of an element
of an element
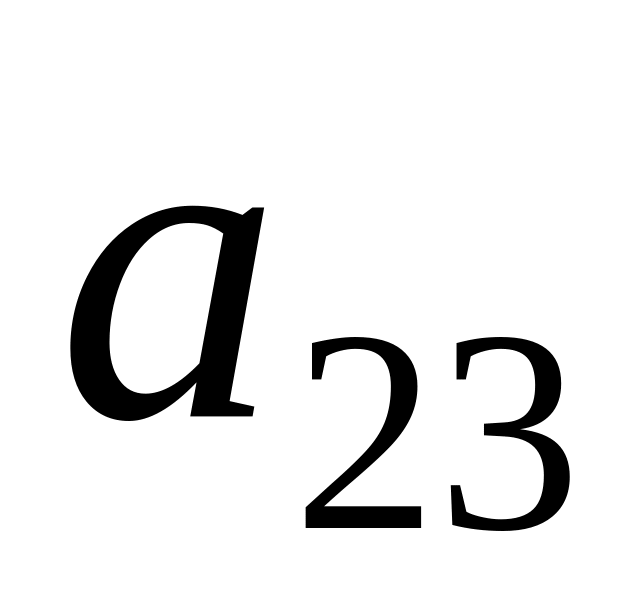 of a matrix
of a matrix
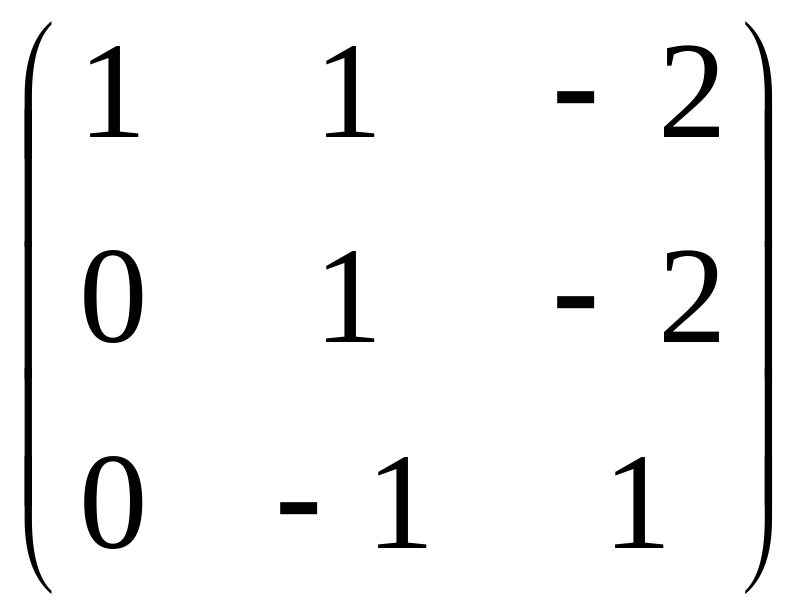 .
.Minor is:
Calculate product of matrices:
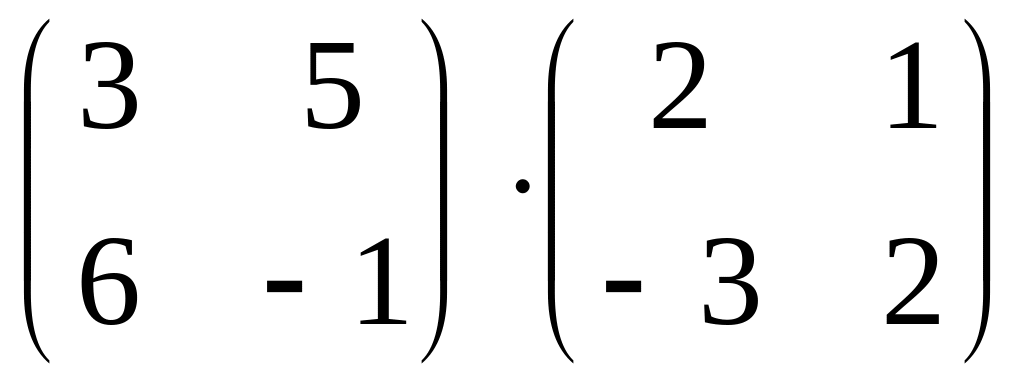 .
.Matrices
 and
and
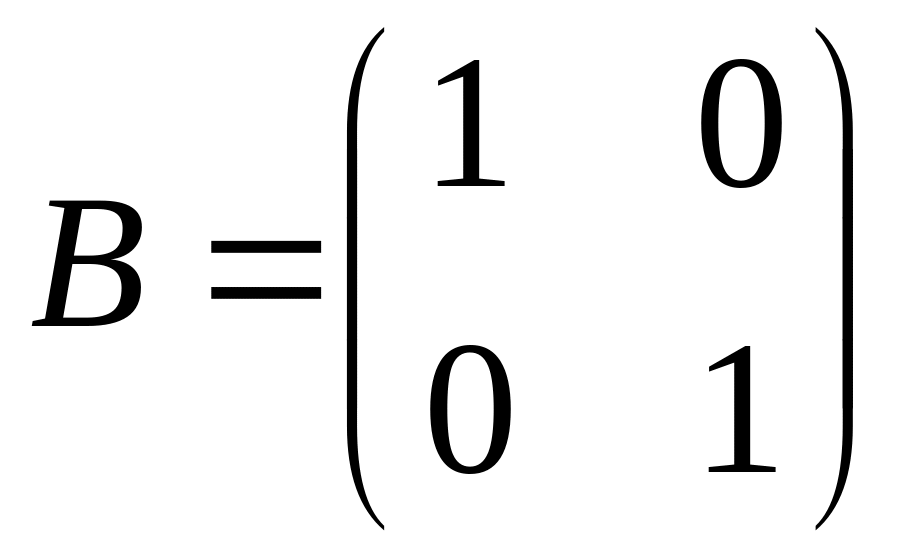 are given. Find product of a matrices
.
are given. Find product of a matrices
.Matrices
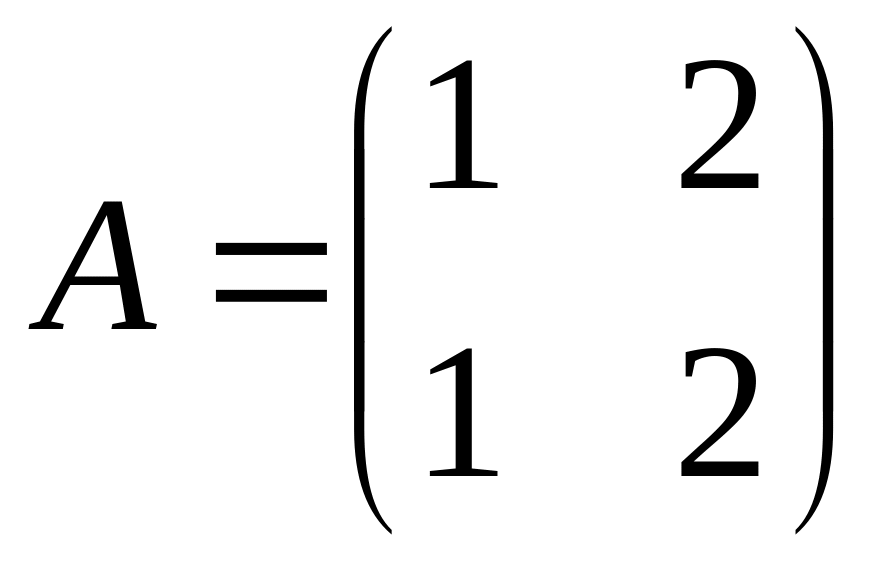 and
and
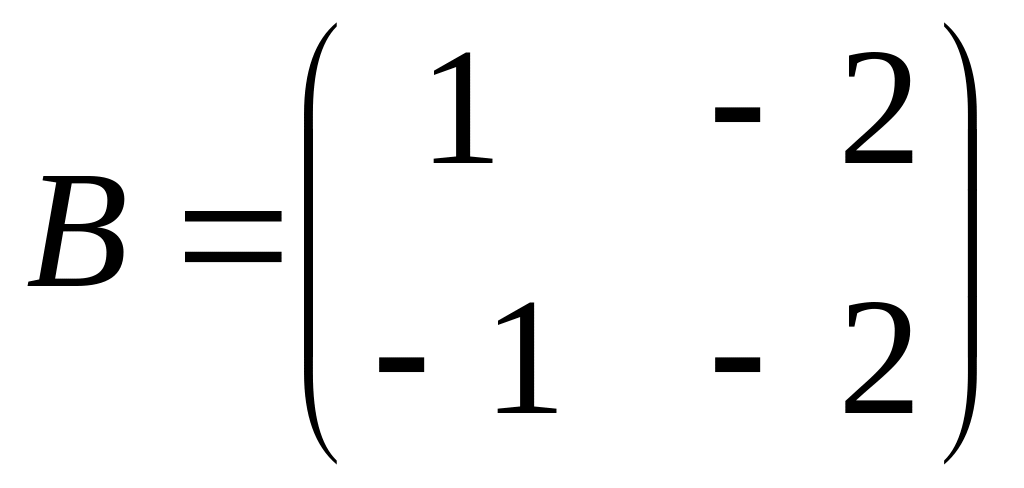 .
Find a difference of matrices
.
Find a difference of matrices
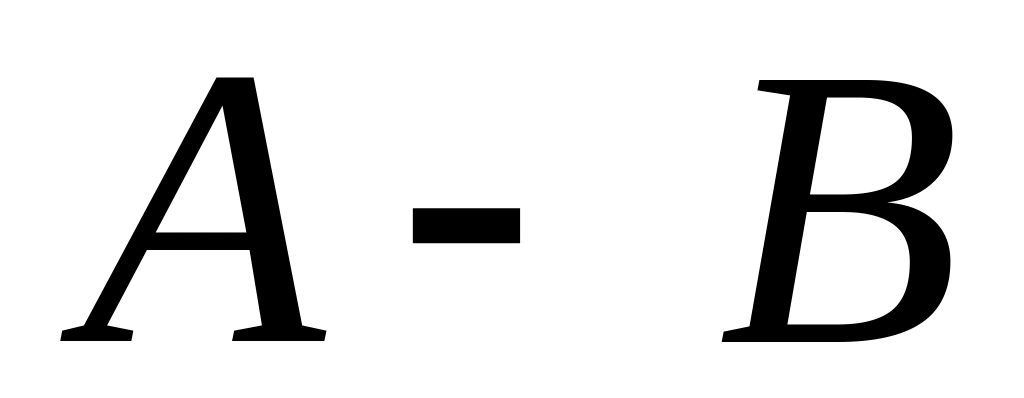 .
.How to add two matrixes?
How to subtract one matrix from another matrix?
Matrices
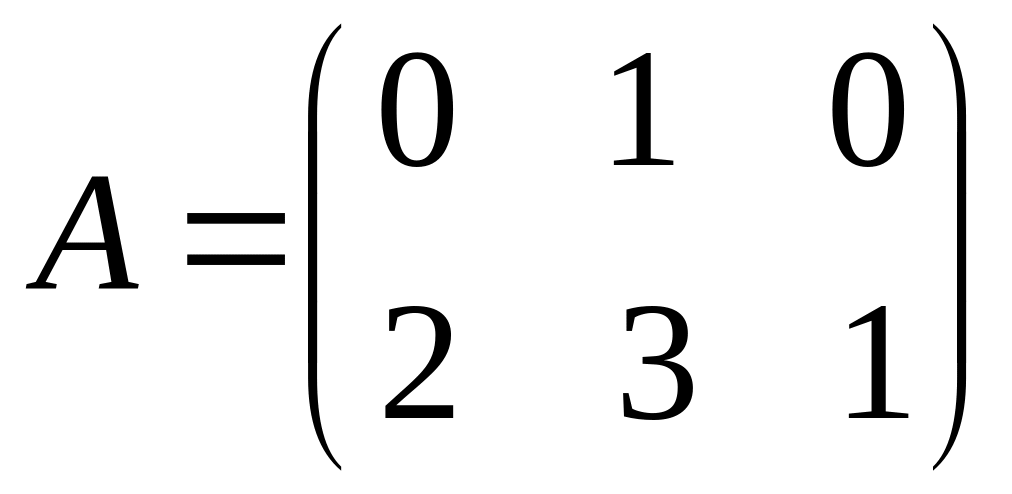 and
and
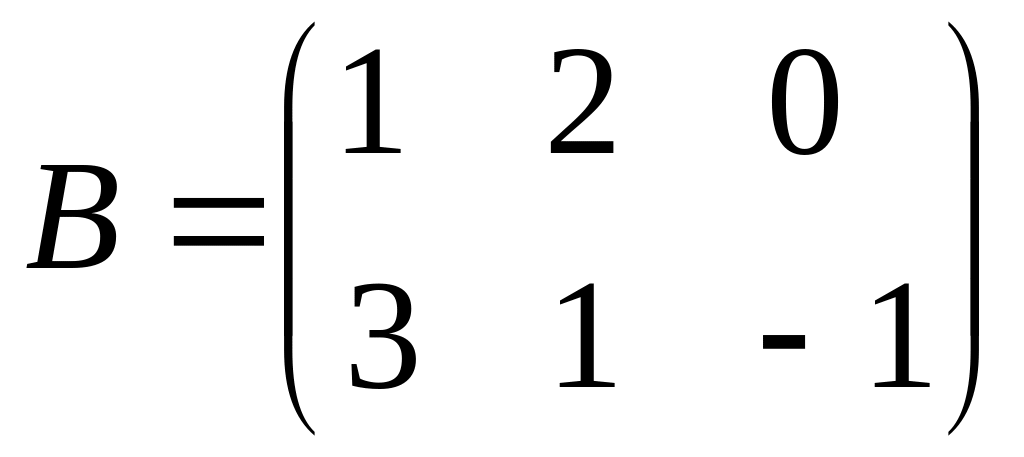 are given. Find
.
are given. Find
.Matrices
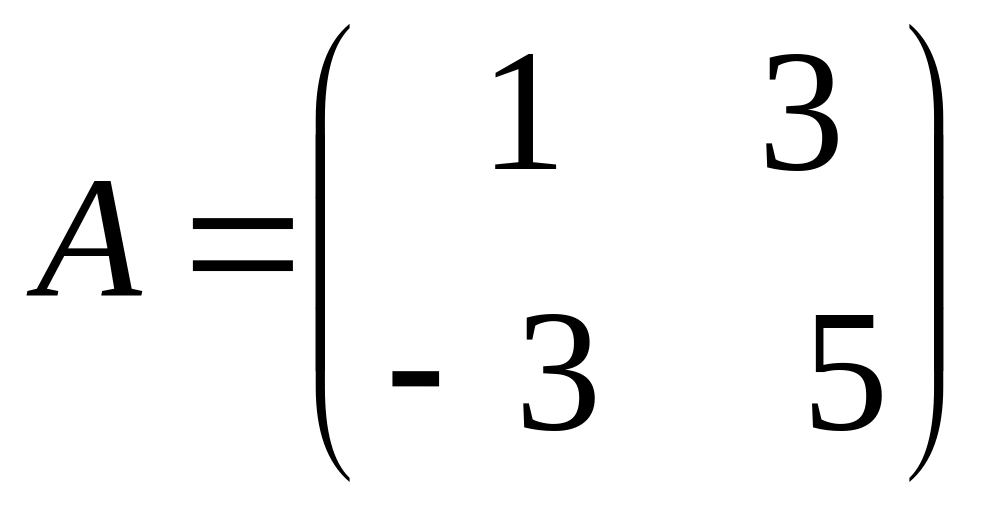 and
and
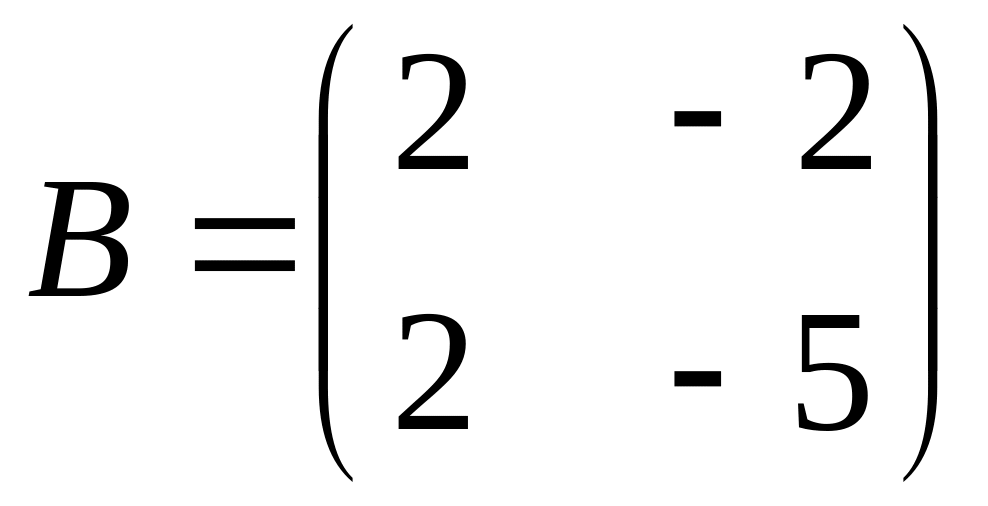 are given. Find
.
are given. Find
.Calculate
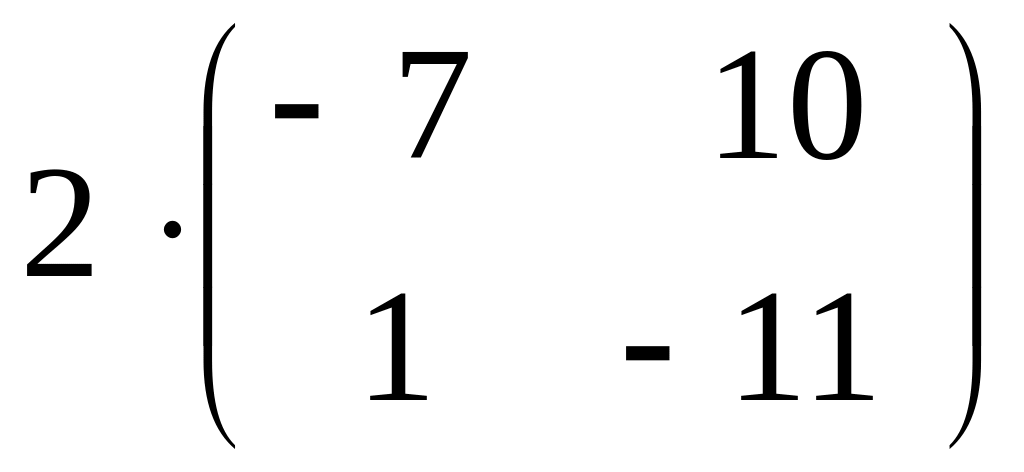 .
.Calculate a determinant
 .
.Calculate a determinant
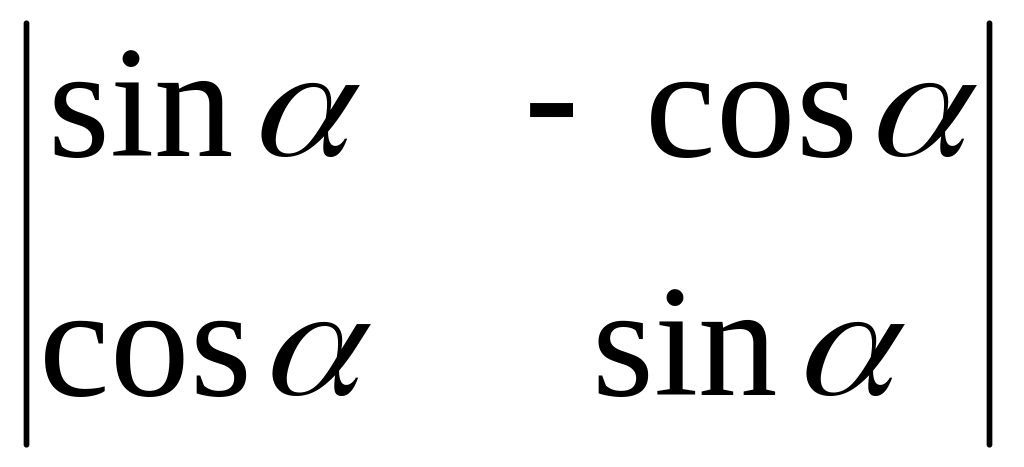 .
.
Theme 2. Systems of the linear equations
Solve system of the equations
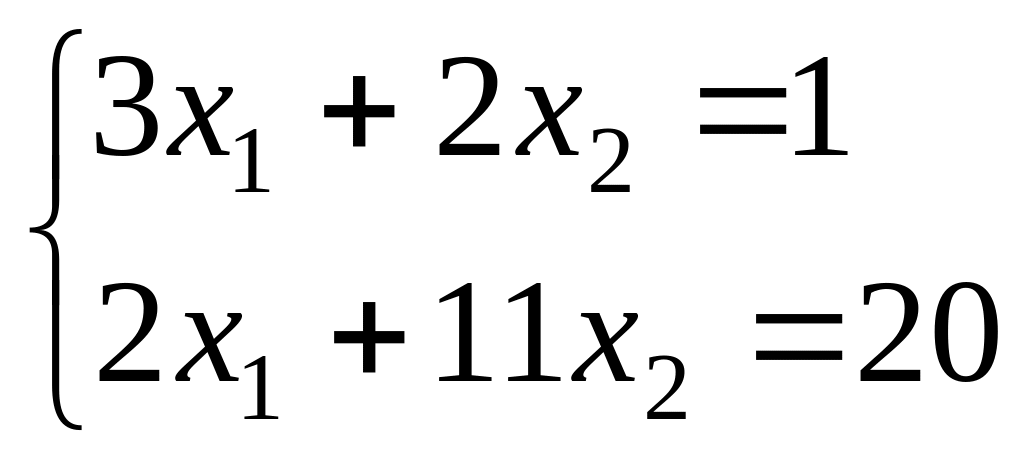 .
Find
.
Find
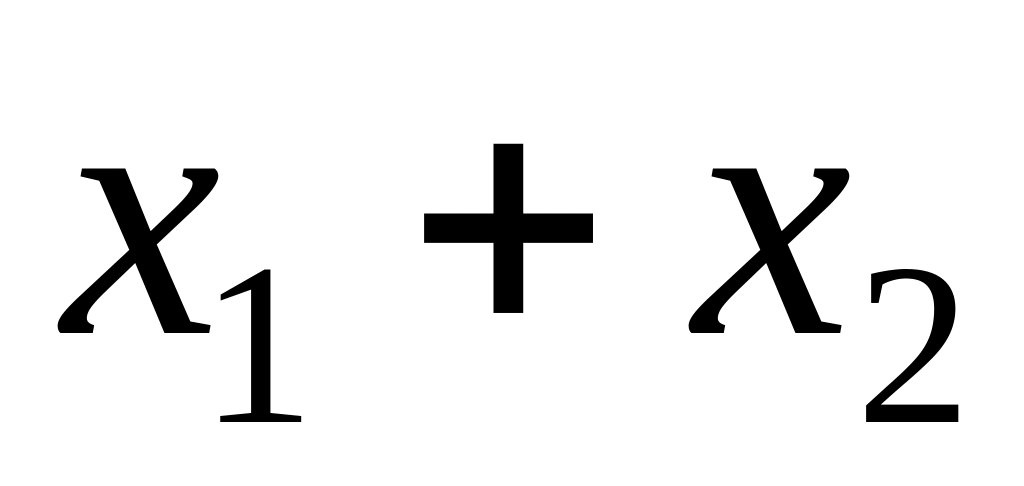 .
.Solve system of the equations
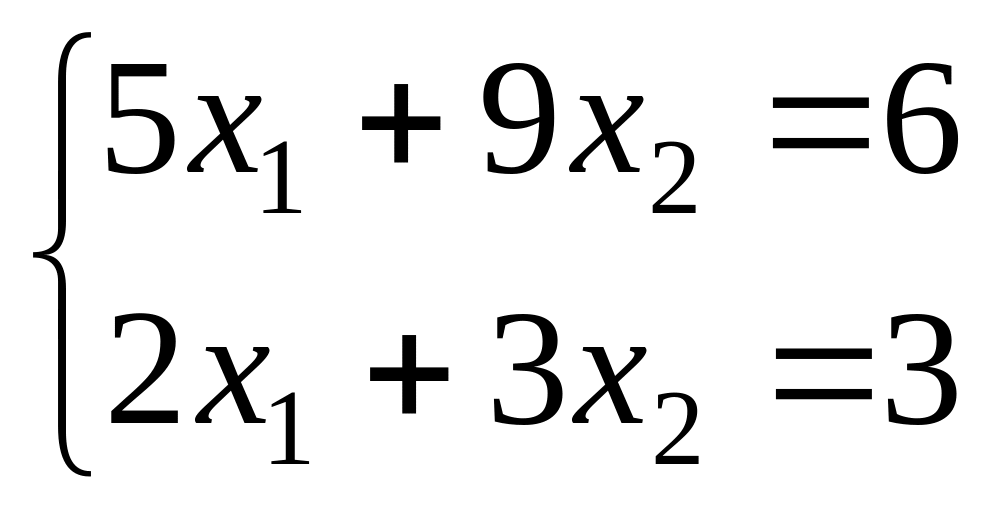 .
Find
.
.
Find
.Solve system of the equations
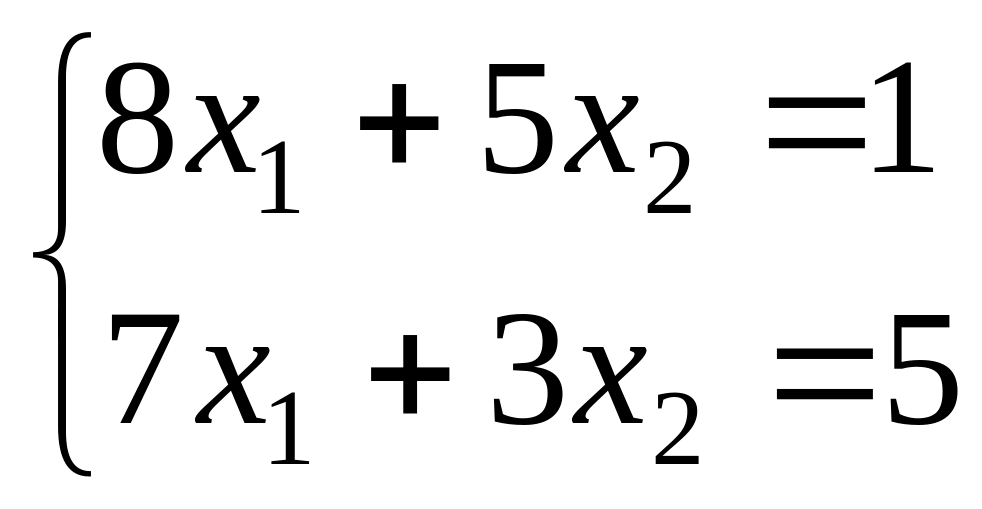 .
Find
.
.
Find
.Solve system of the equations
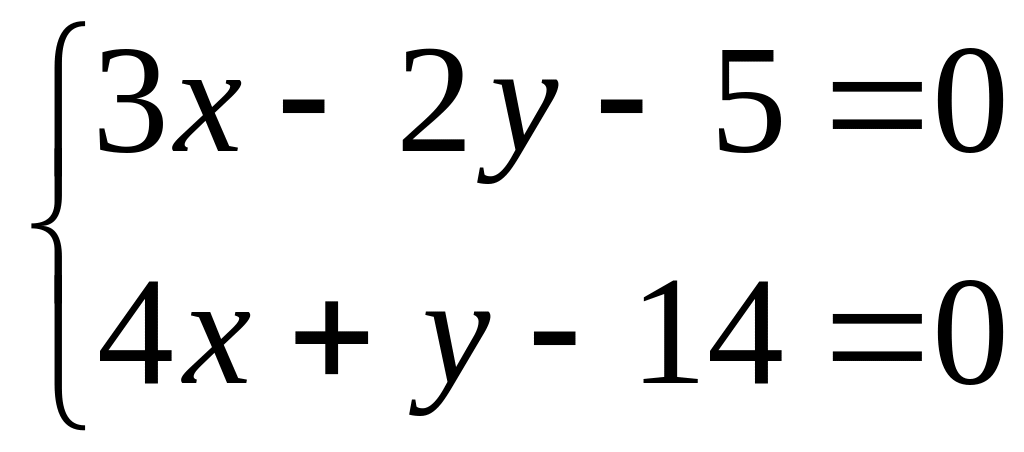 .
Find
.
Find
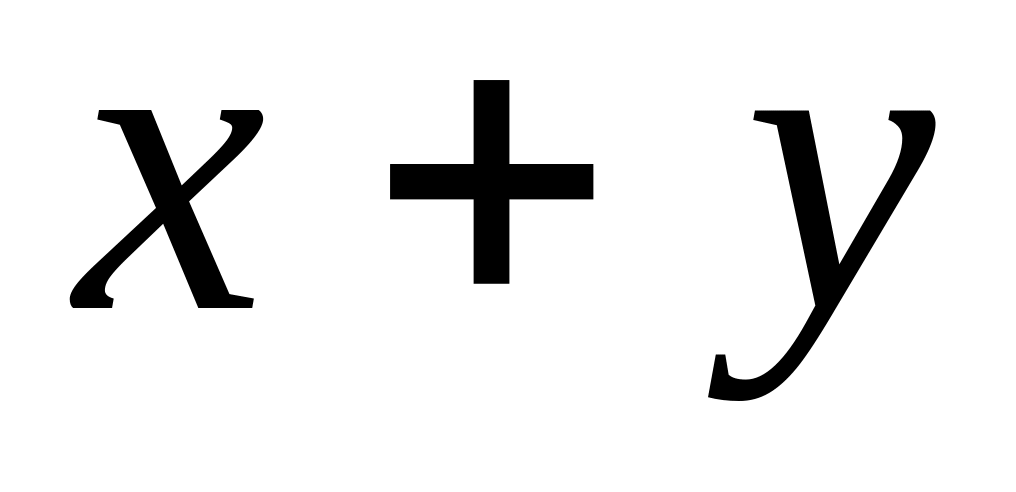 .
.If the determinant of a matrix of system of the
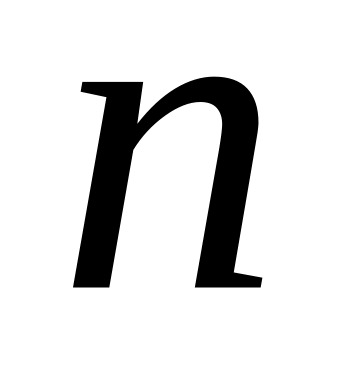 linear
equations from
unknown
variables is different from zero, then system of the equations :
linear
equations from
unknown
variables is different from zero, then system of the equations :Solve system of the equations
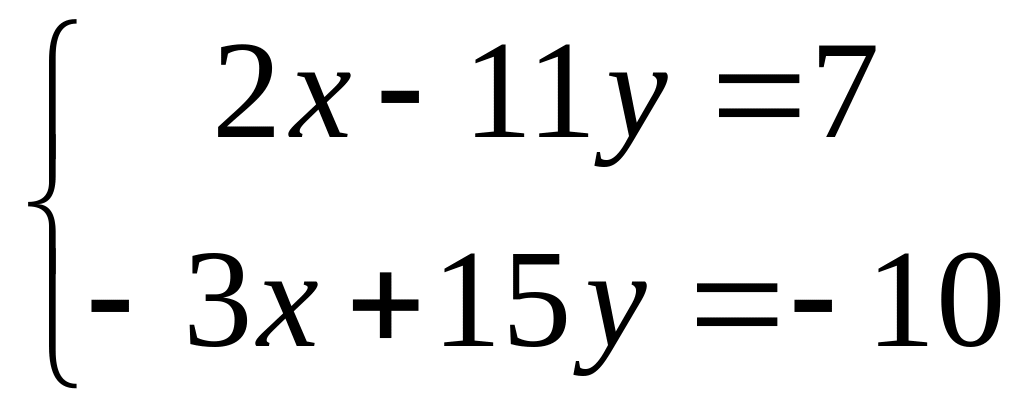 by Kramer's formulas. Find
by Kramer's formulas. Find
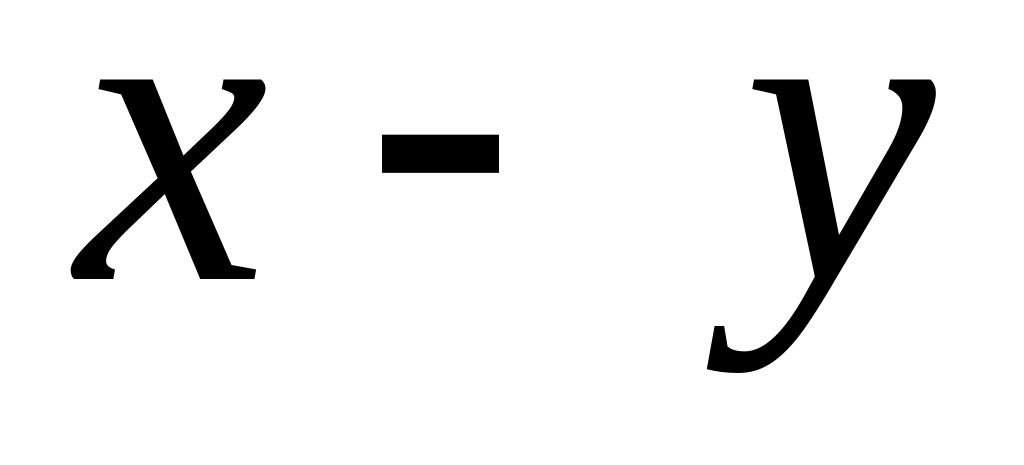 .
.Find symbolical record of Kramer’s formulas, defining the decision of system if the determinant
 of a matrix of system is not equal to zero.
of a matrix of system is not equal to zero.System of the linear equations is called compatible, if it:
Solve system of the equations by Kramer's rule
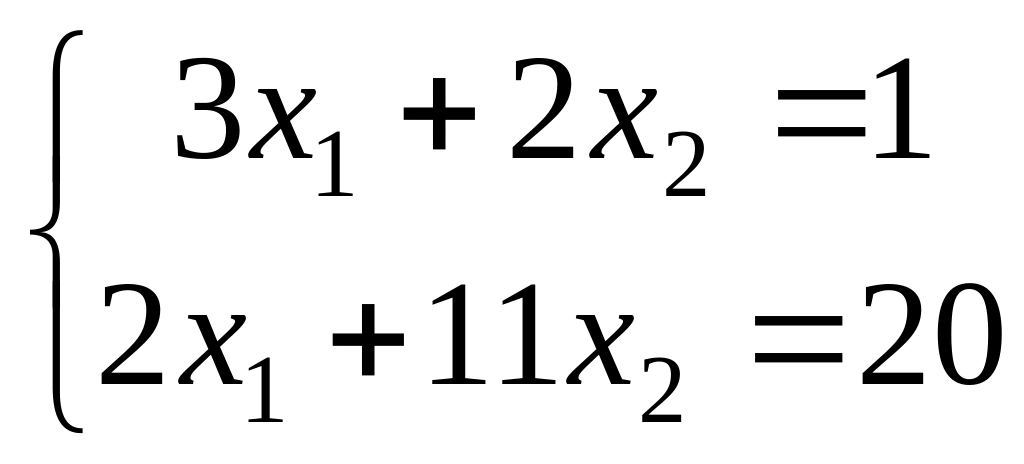 .
Find
.
Find
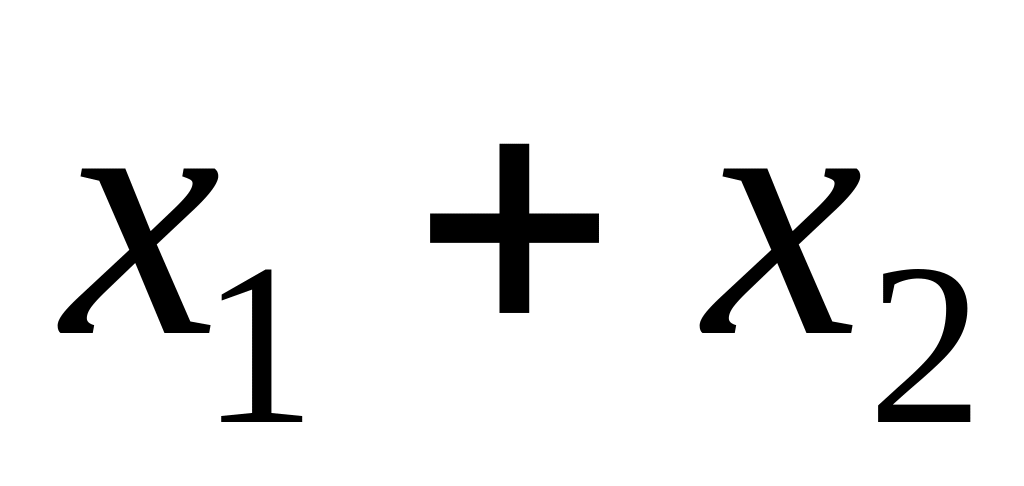 .
.Solve system of the equations
 .
.Solve system of the equations
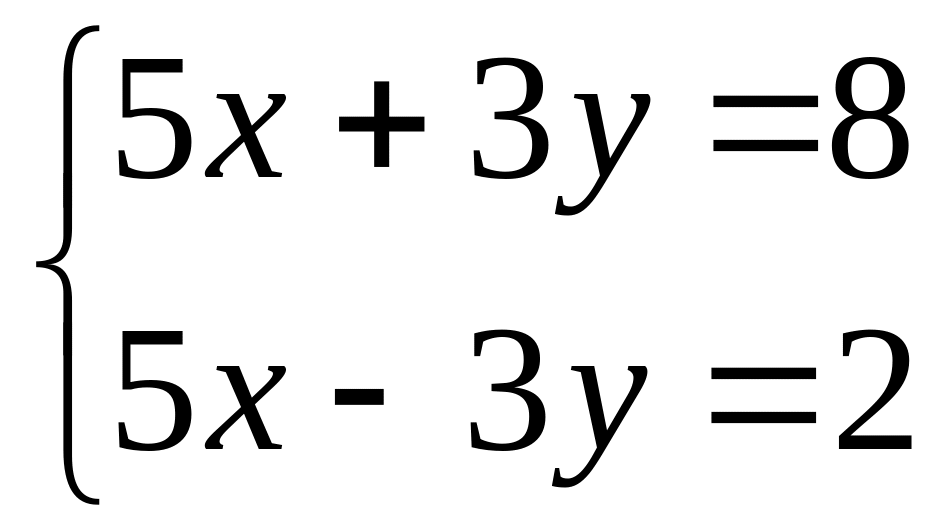 .
.How it is possible to find
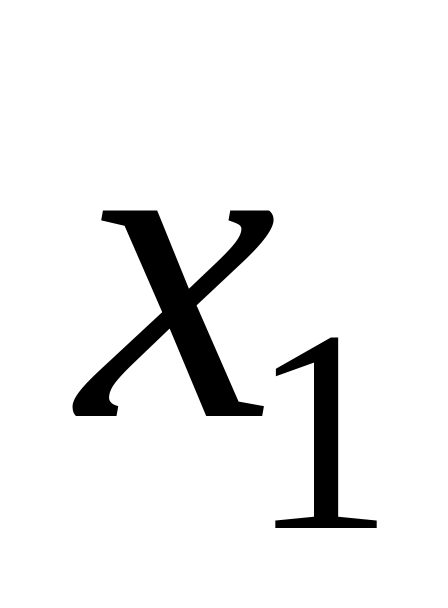 by means of Kramer's formula?
by means of Kramer's formula?How it is possible to find
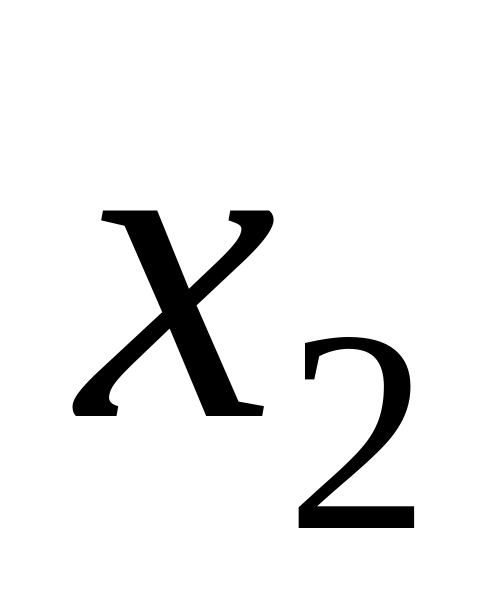 by means of Kramer's formula?
by means of Kramer's formula?How it is possible to find
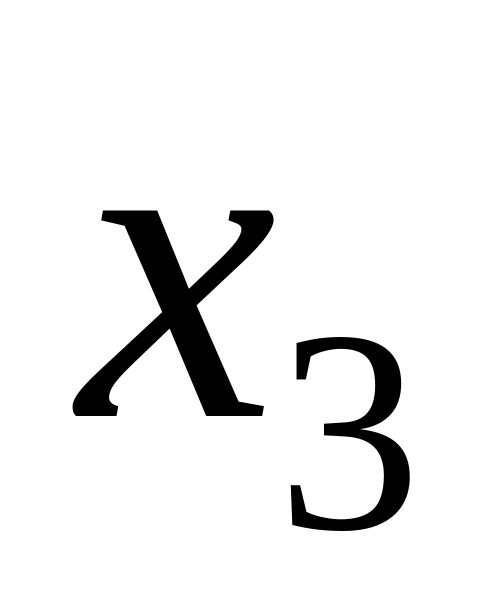 by means of Kramer's formula?
by means of Kramer's formula?What from the specified formulas below is Kramer's formula?
Solve system of the equations
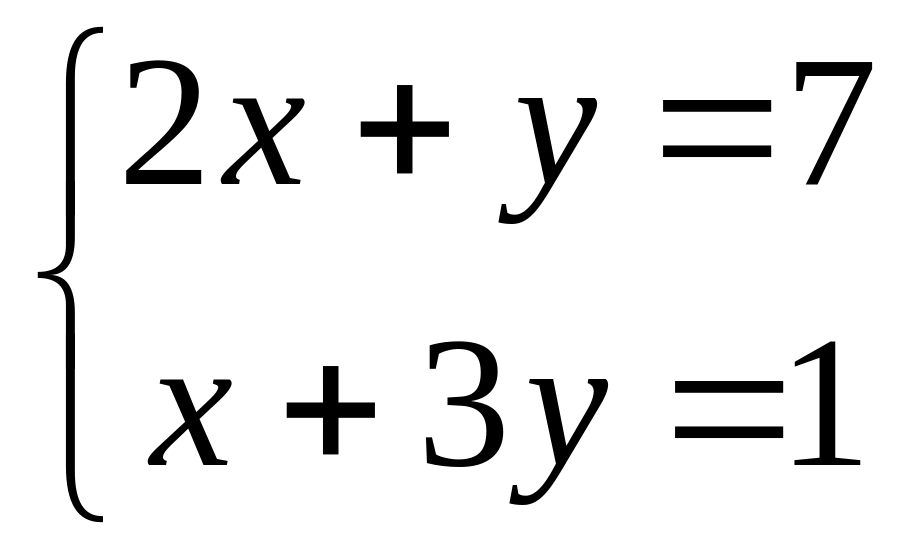 ,
using Kramer's rule.
,
using Kramer's rule.Solve system of the equations
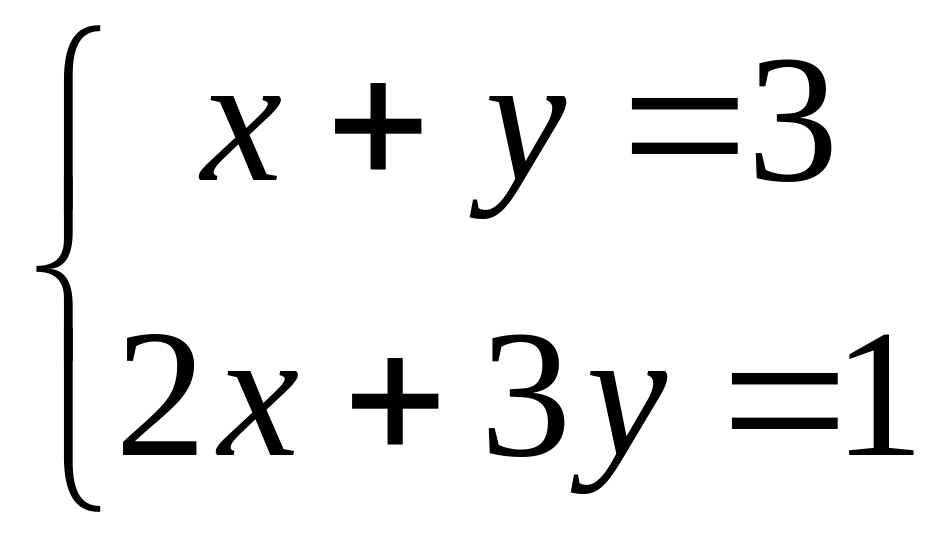 ,
using Kramer's rule.
,
using Kramer's rule.Solve system of the linear equations
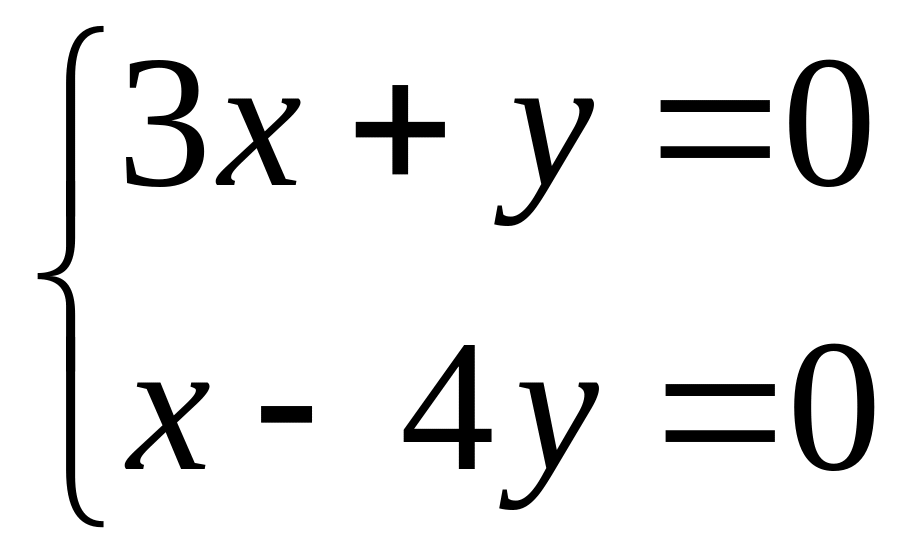 .
.Solve system of the linear equations
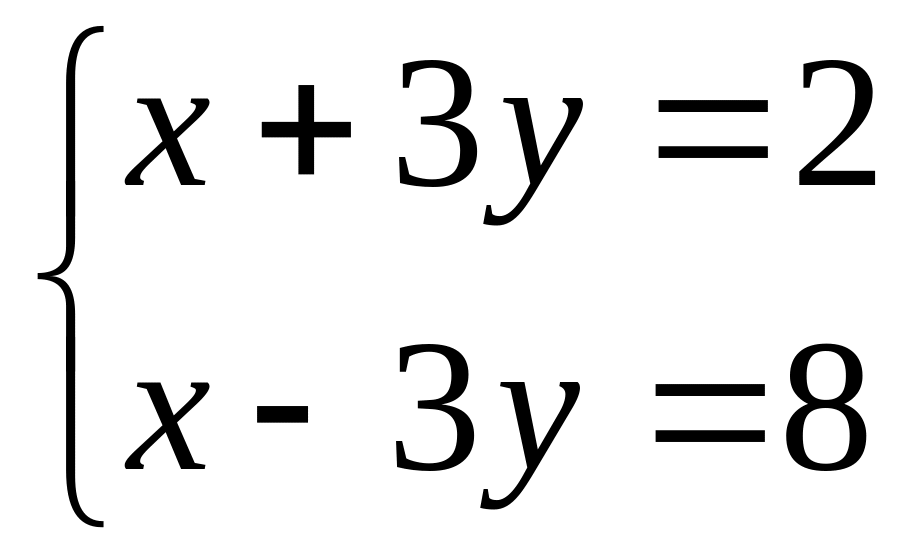 .
.Solve system of the linear equations
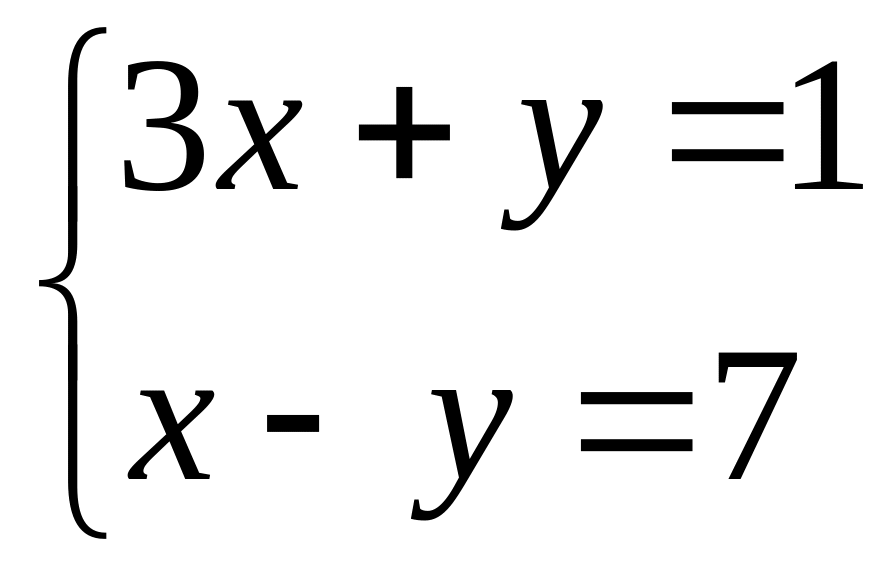 .
.
Theme 3. Elements of vector algebra
Points
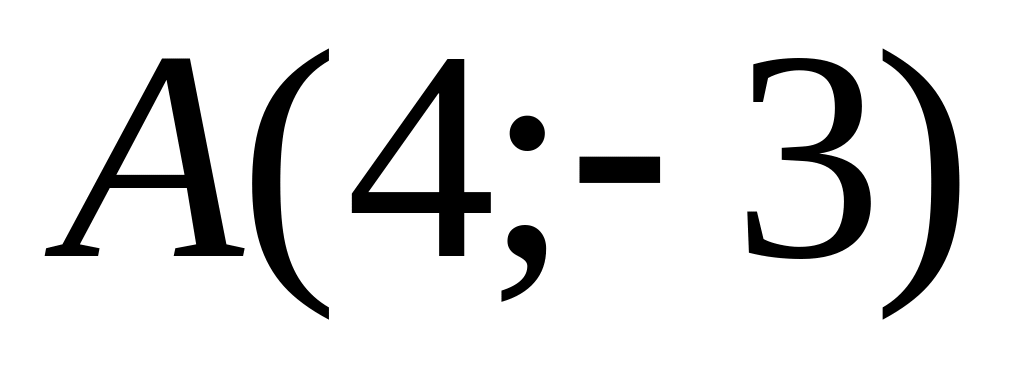 and
and
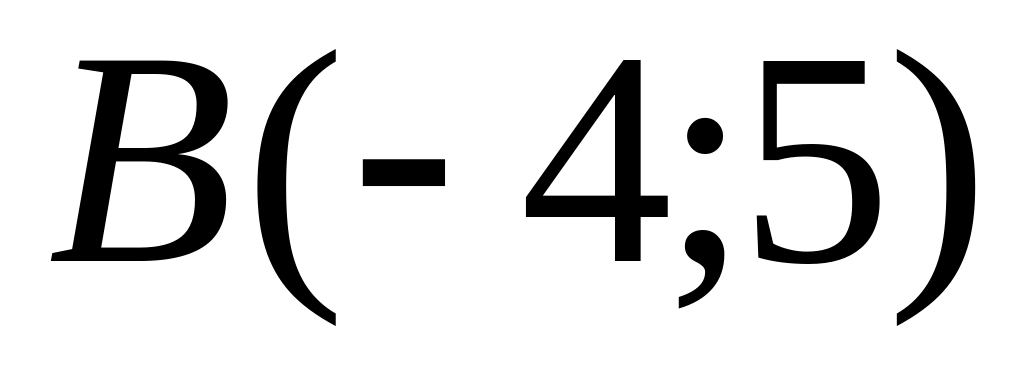 are given. Find coordinates of a vector
are given. Find coordinates of a vector
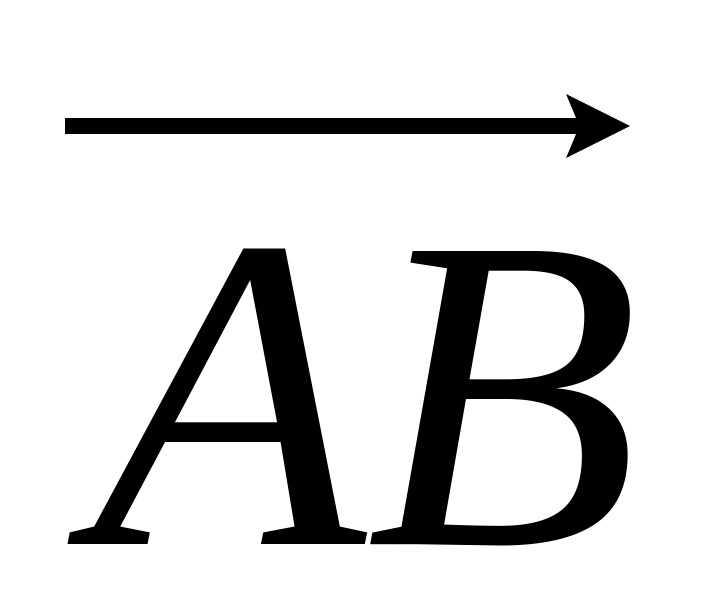 .
.Find length of a vector
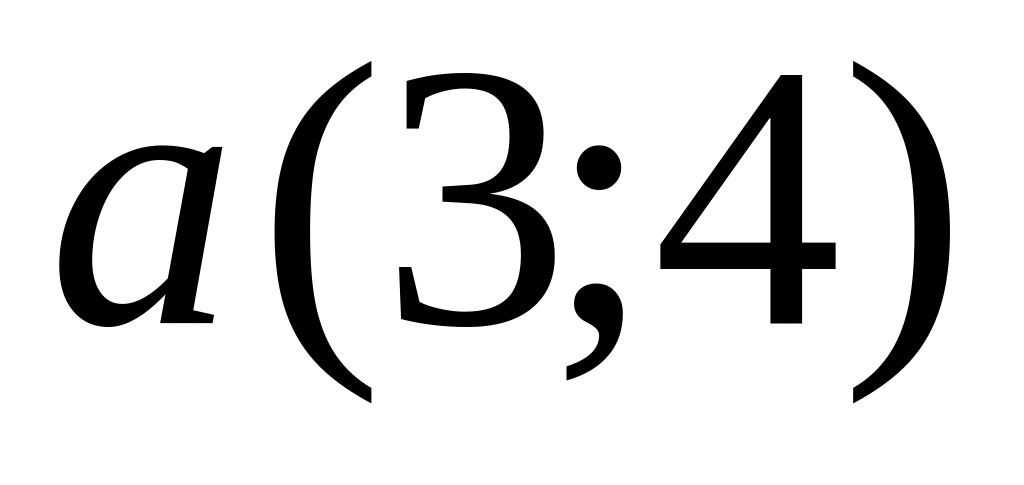 .
.Vectors
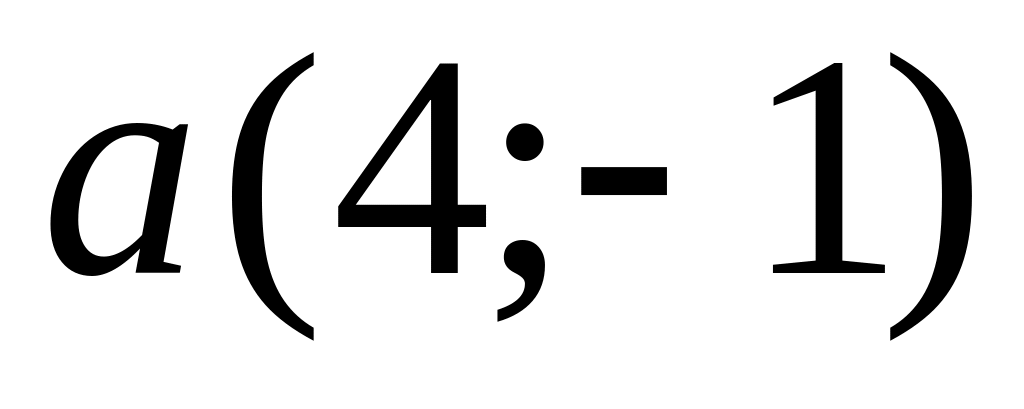 and
and
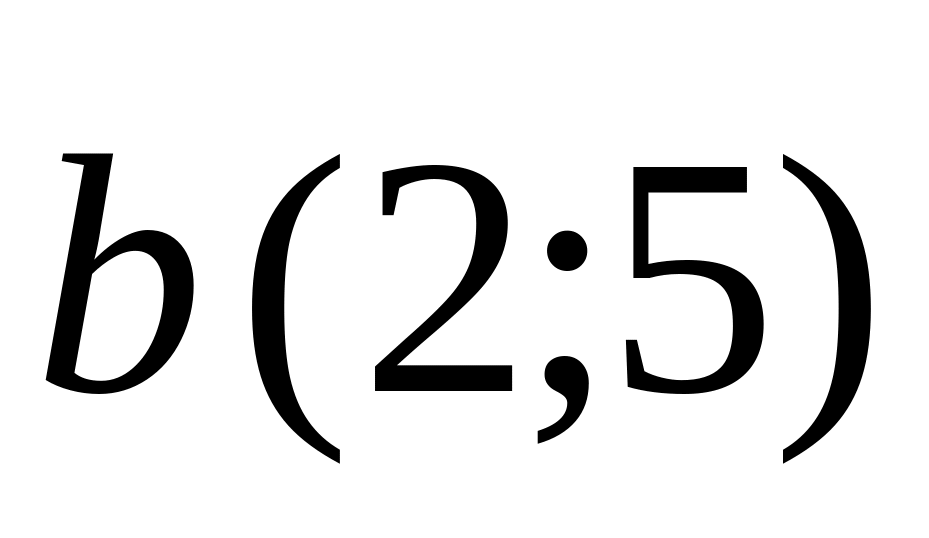 are given. Find coordinates of a vector
are given. Find coordinates of a vector
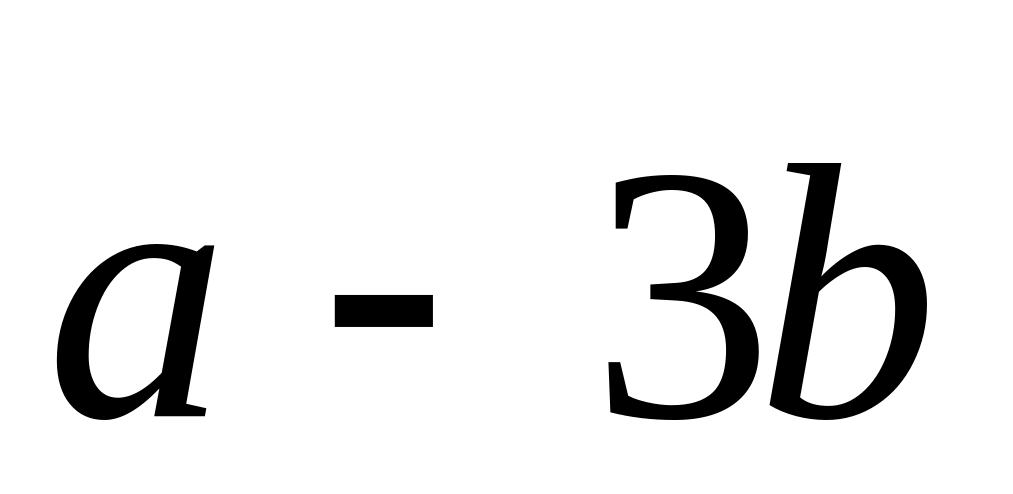 .
.Find scalar product of vectors and
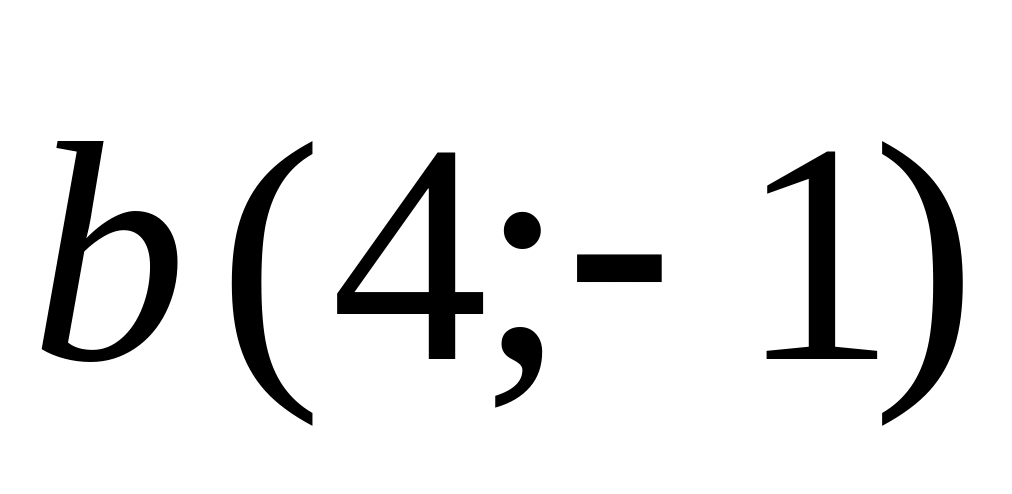 .
.Find an angle between vectors
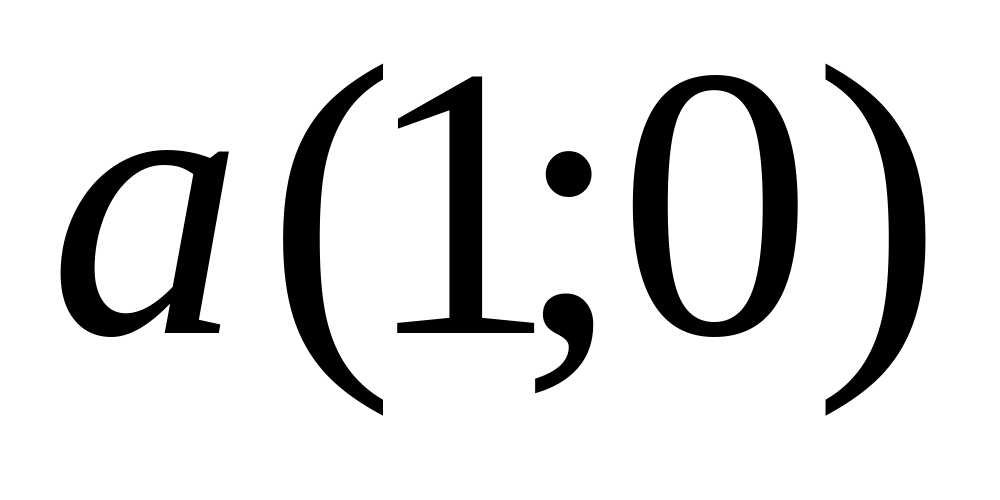 and
and
 .
.At what value
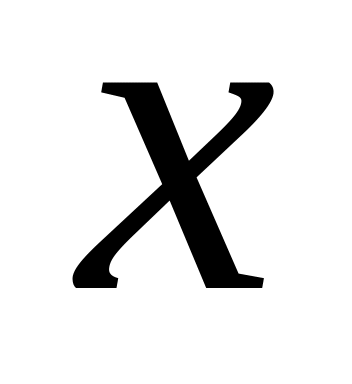 vectors
vectors
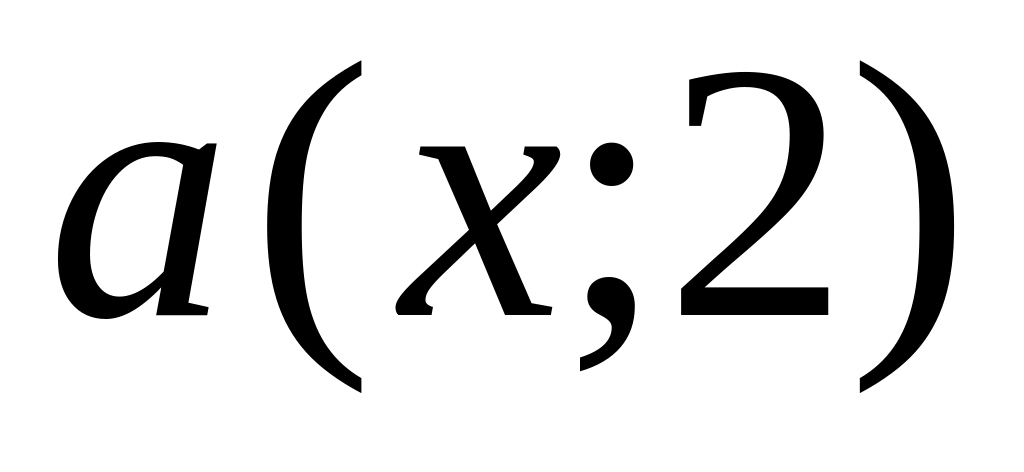 and
and
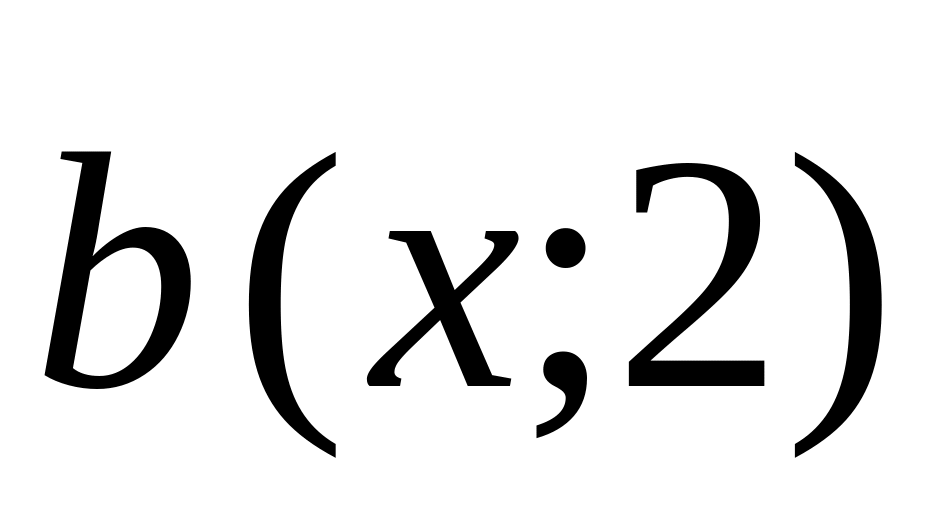 are collinear?
are collinear?At what value vectors and
 are orthogonal?
are orthogonal?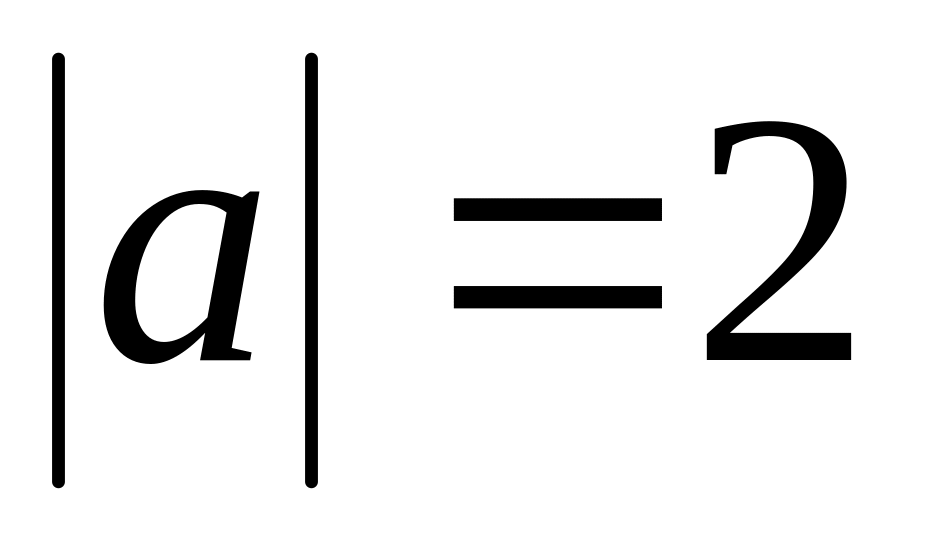 ,
,
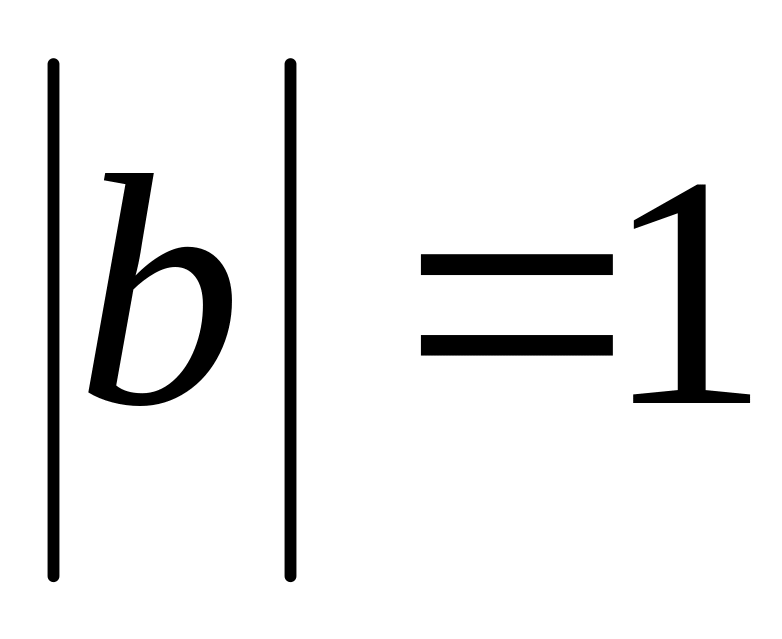 ,
an angle between
,
an angle between
 and
and
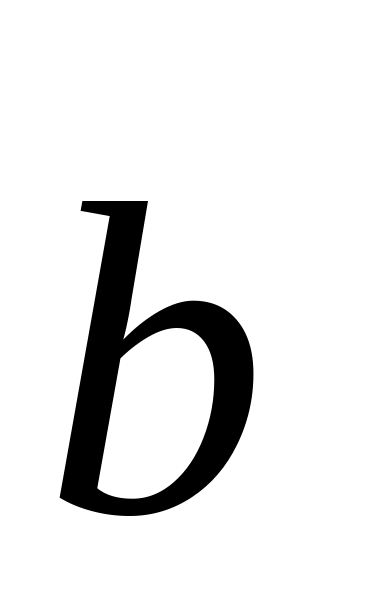 is
equal
is
equal
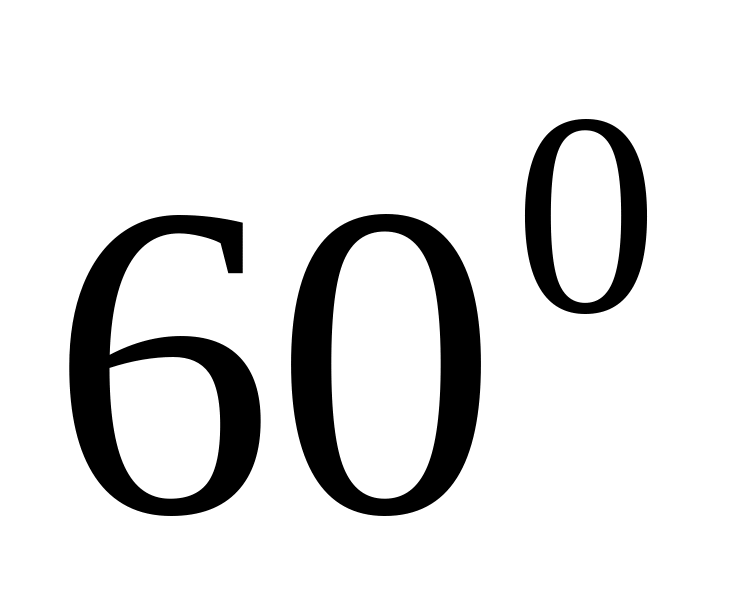 .
Find scalar product
.
Find scalar product
 .
.Points
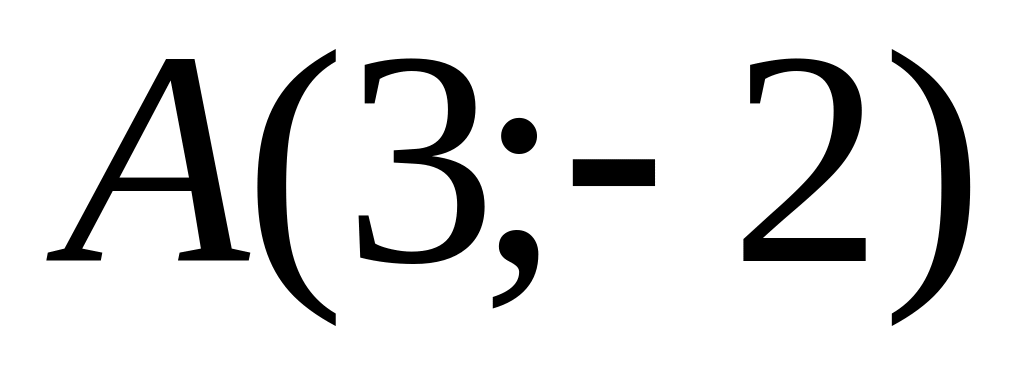 and
and
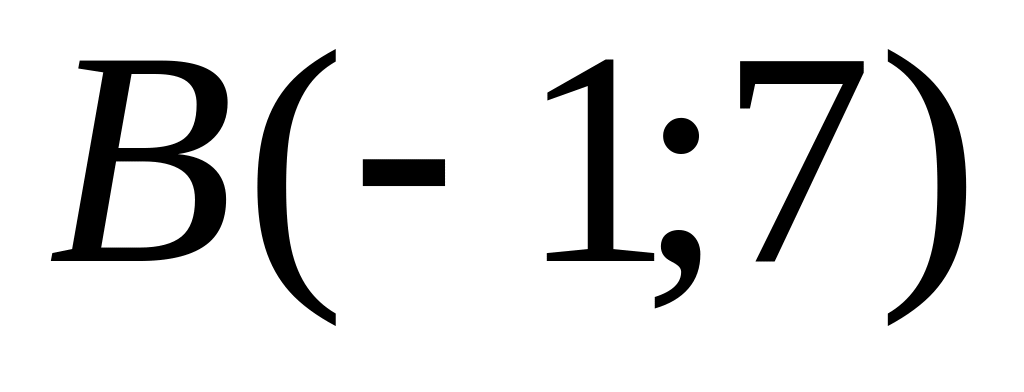 are given. Find coordinates of a vector
.
are given. Find coordinates of a vector
.Find length of a vector
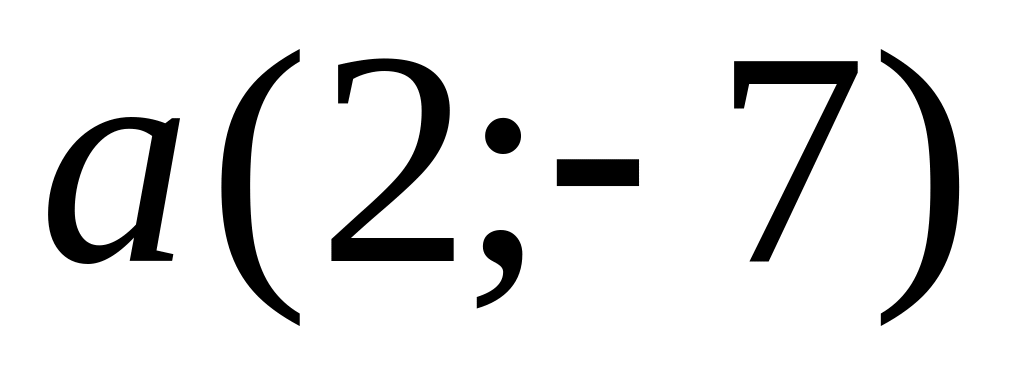 .
.Vectors
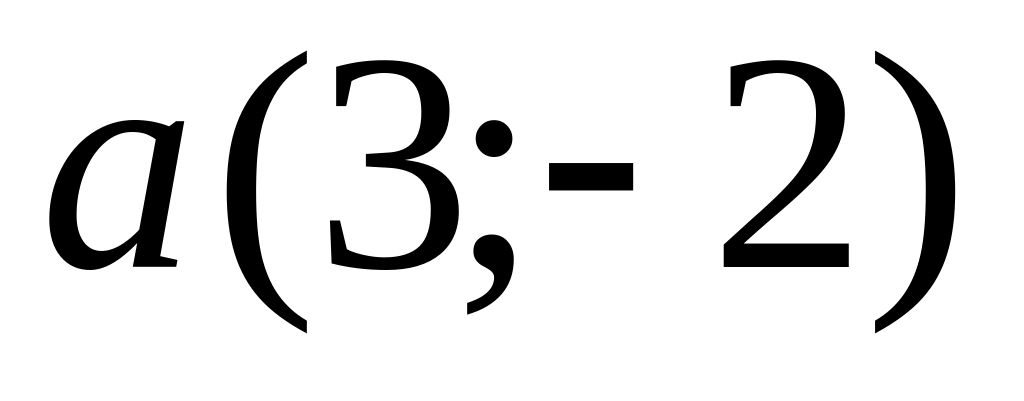 and
and
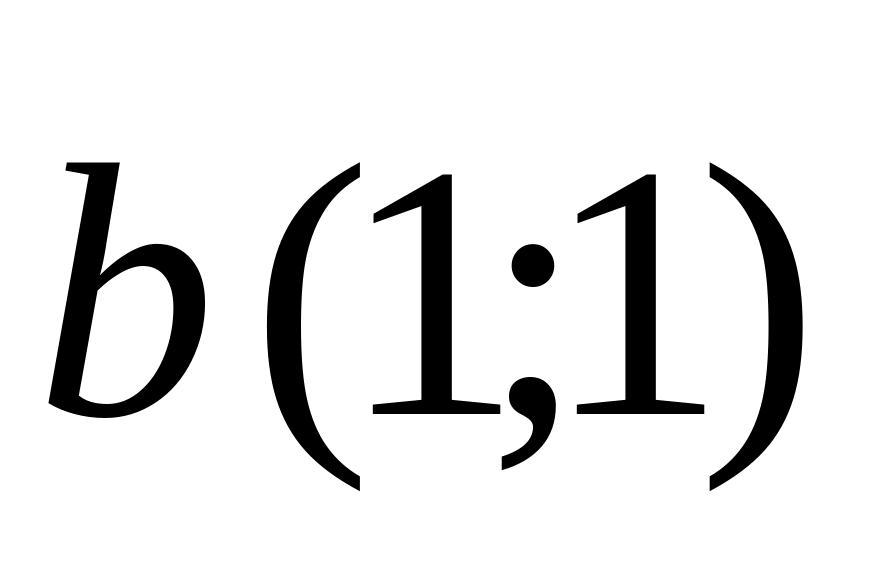 are given. Find coordinates of a vector
are given. Find coordinates of a vector
 .
.Find scalar product of vectors
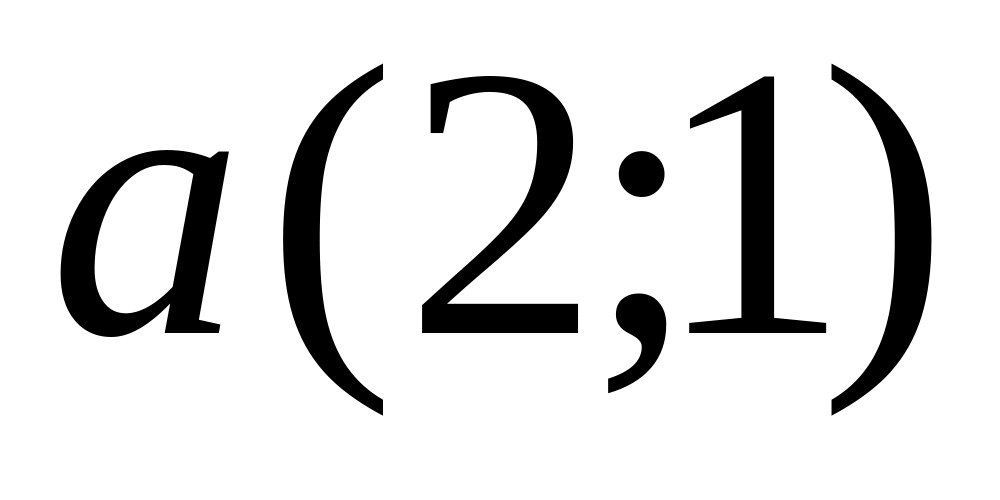 and
and
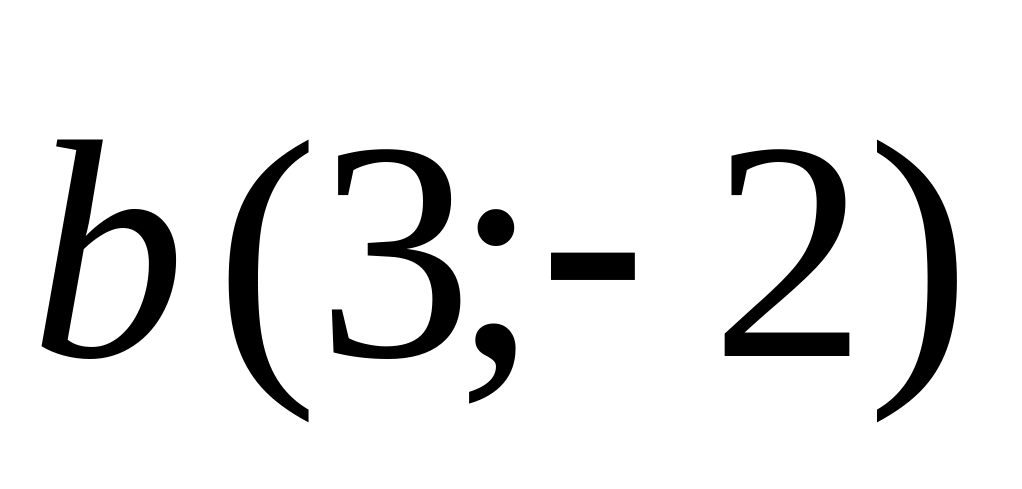 .
.Find an angle between vectors
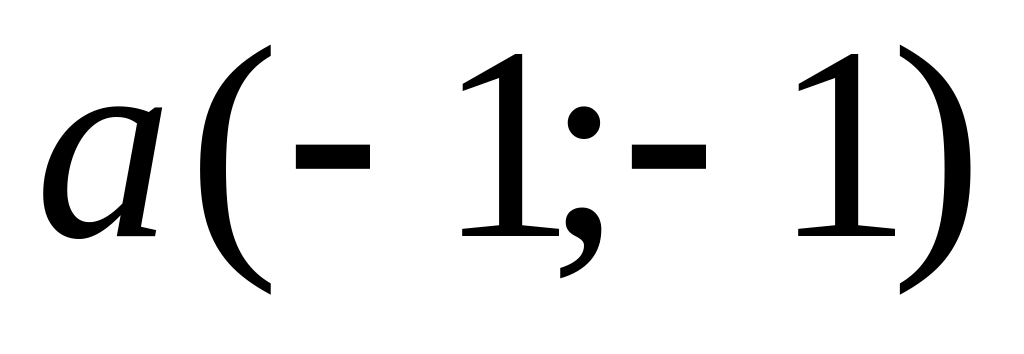 and
and
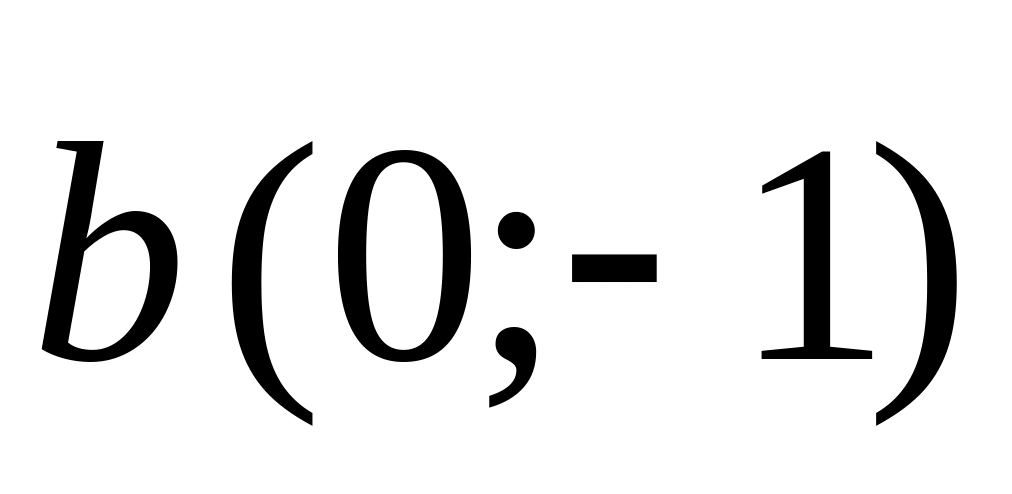 .
.At what value
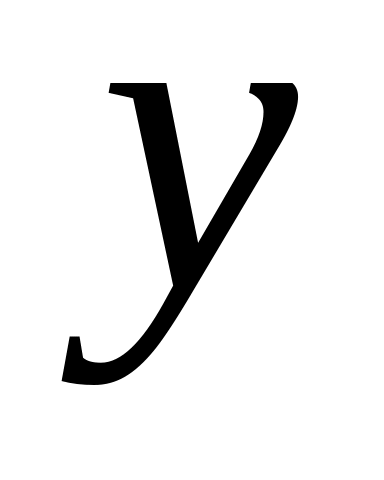 vectors
vectors
 and
and
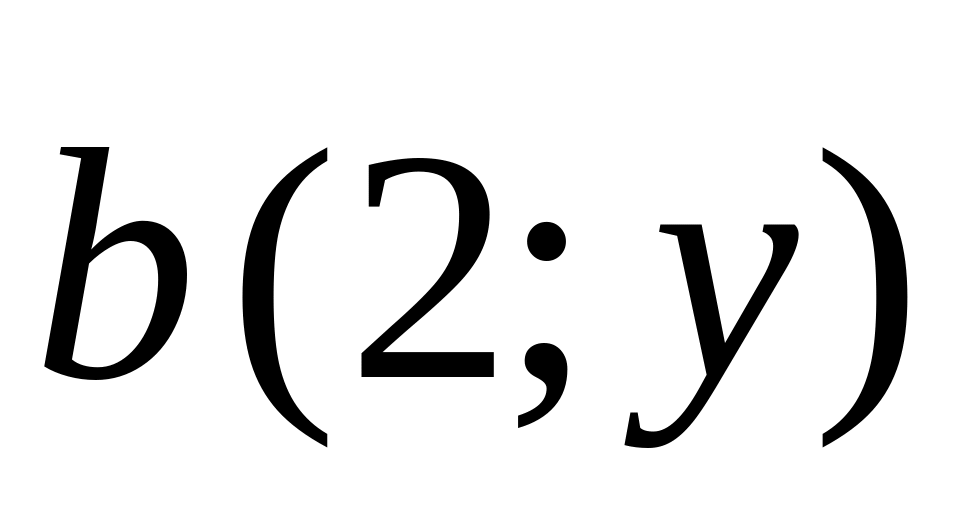 are collinear?
are collinear?At what value vectors
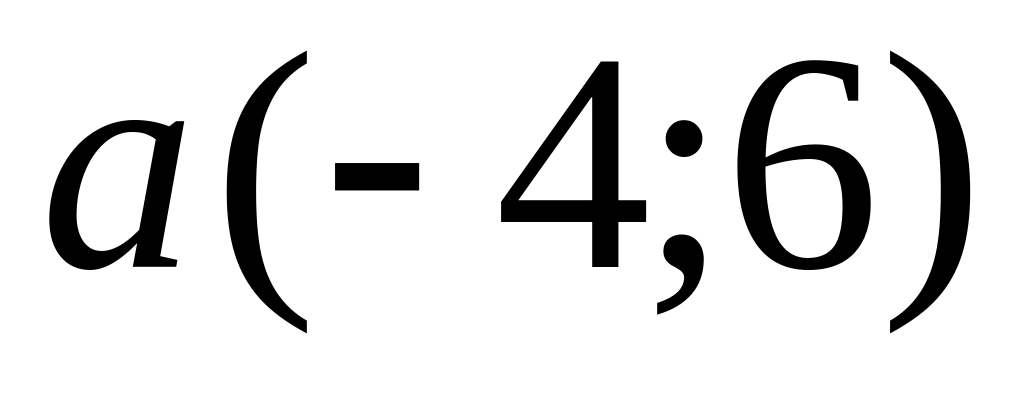 and
are orthogonal?
and
are orthogonal?Points
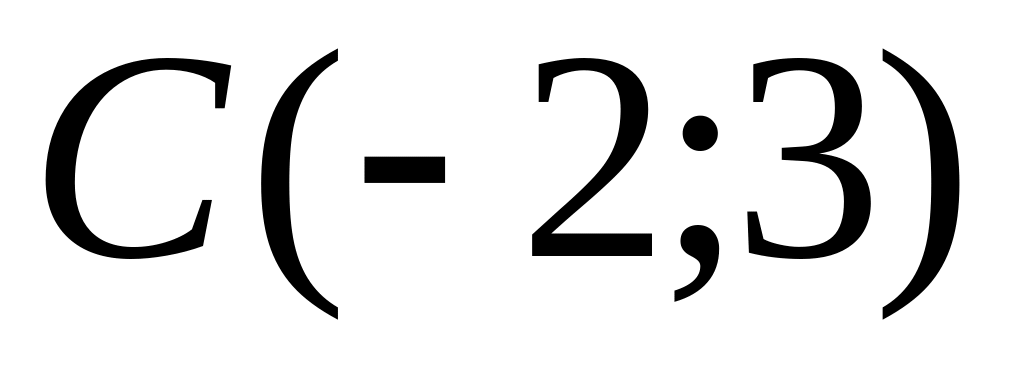 and
and
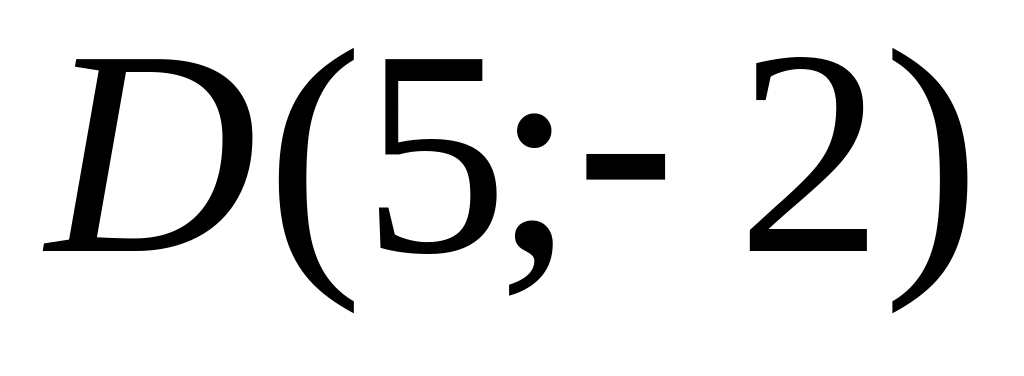 are given. Find coordinates of a vector
are given. Find coordinates of a vector
 .
.Find length of a vector
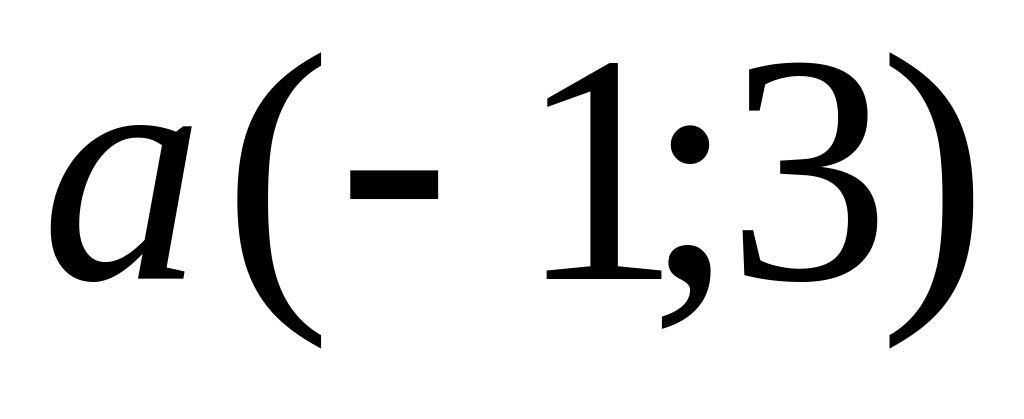 .
.Vectors and are given. Find coordinates of a vector
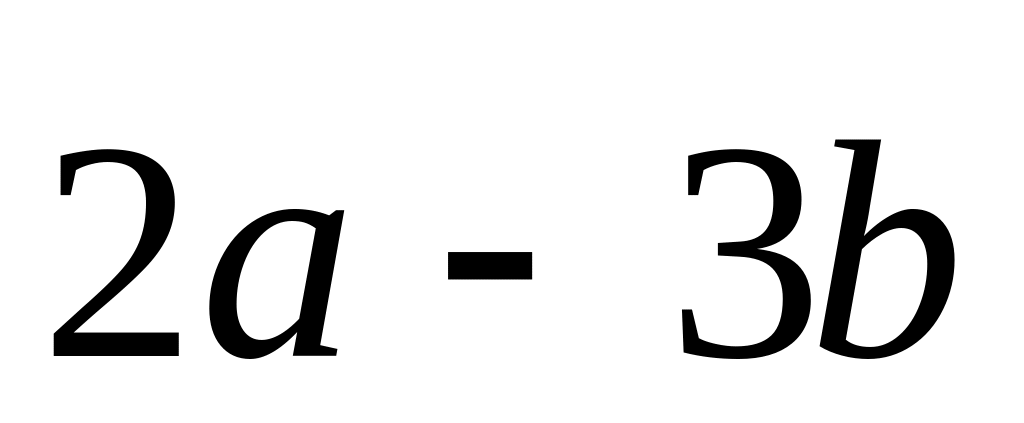 .
.Find scalar product of vectors and
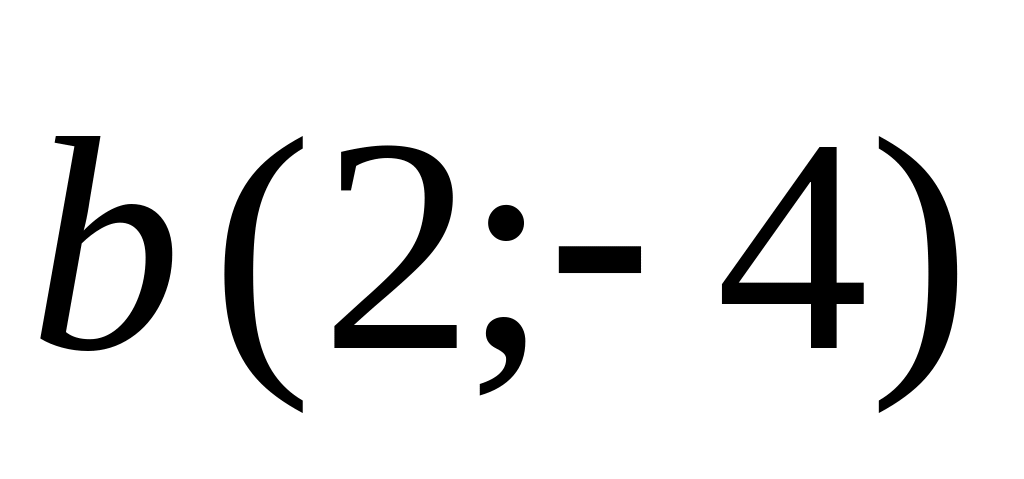 .
.Find an angle between vectors
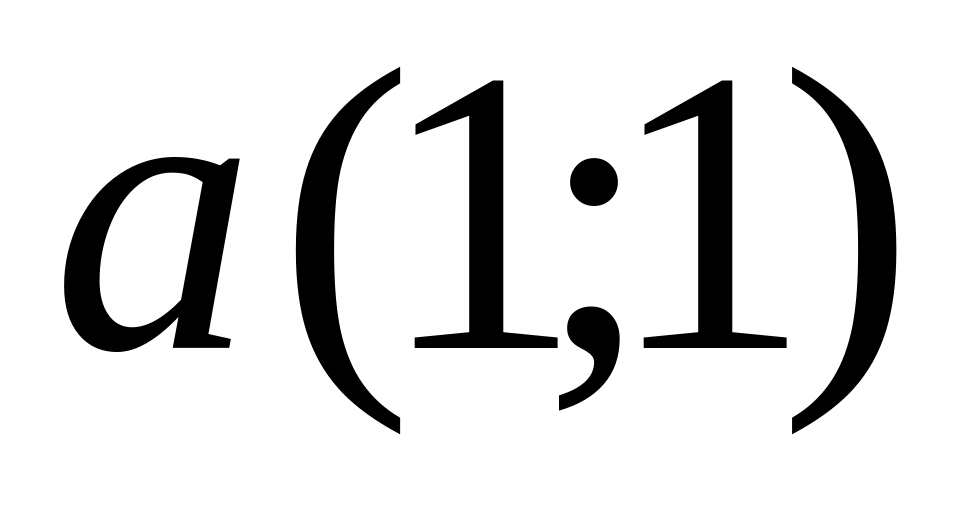 and
.
and
.At what value vectors
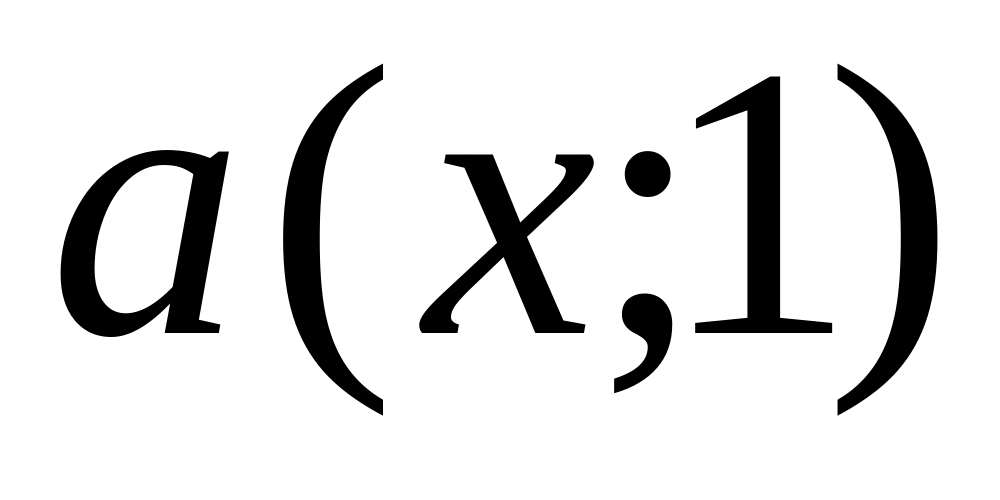 and
and
 are collinear?
are collinear?At what value vectors and
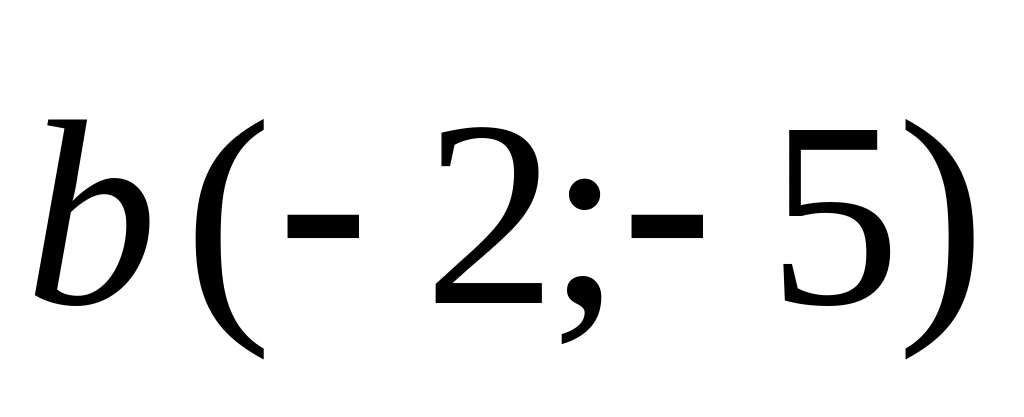 are
orthogonal?
are
orthogonal?Vector, located on one straight line or parallel straight lines are called:
If vector have identical directions and length they are called:
Points
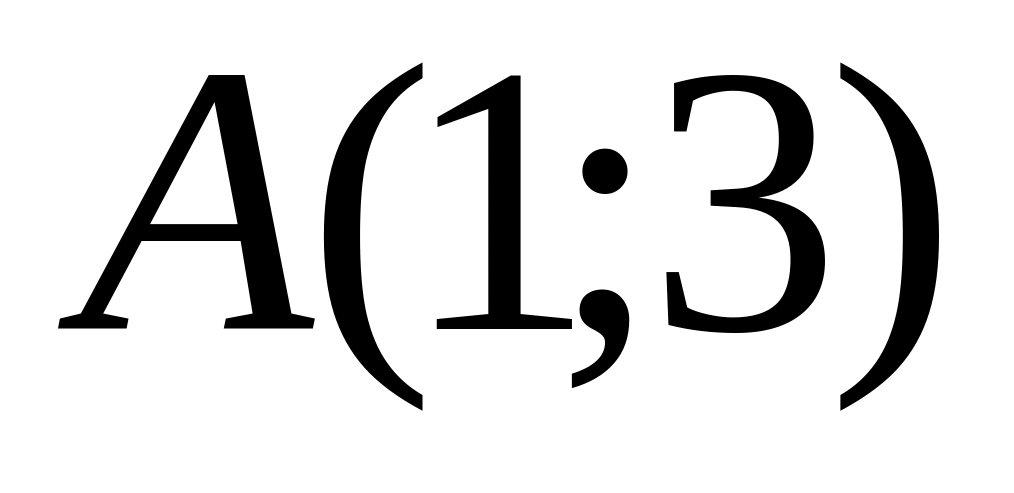 and
and
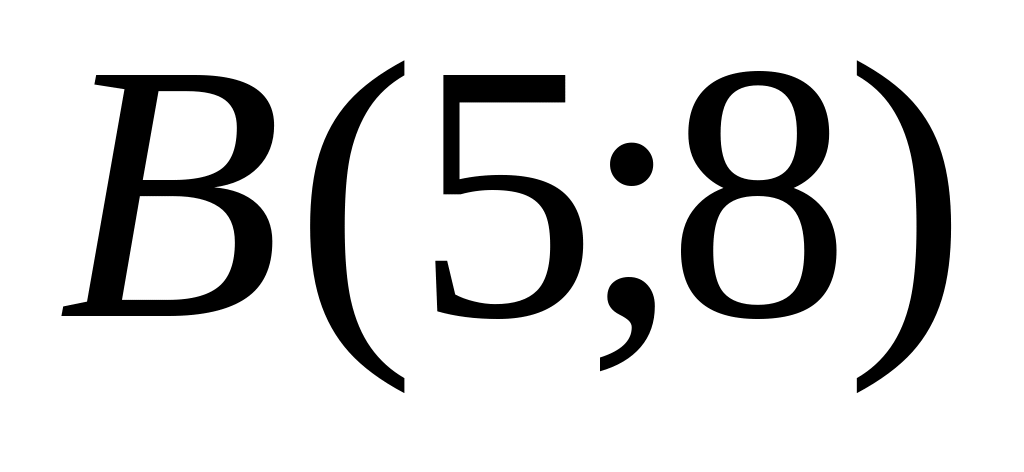 are given. Find coordinates of a vector
.
are given. Find coordinates of a vector
.Find length of a vector .
Vectors
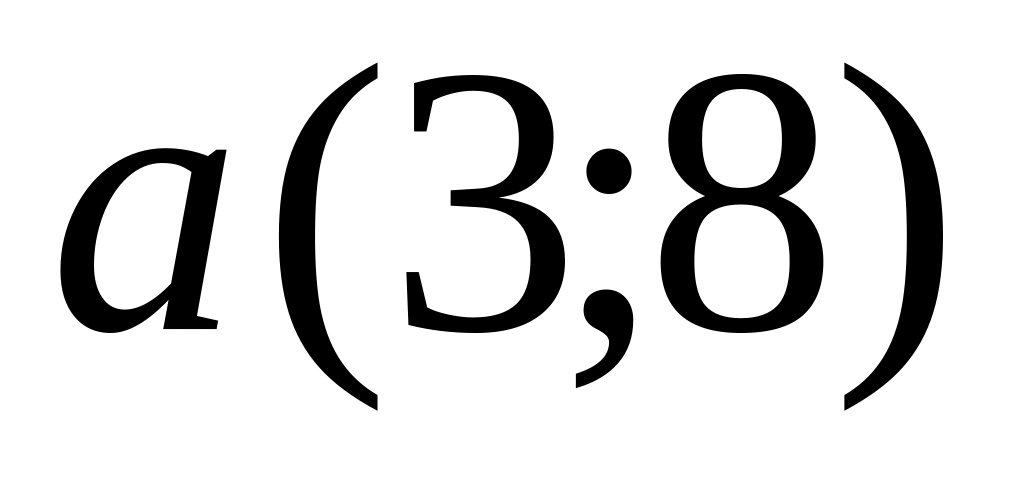 and
and
 are given. Find coordinates of a vector
.
are given. Find coordinates of a vector
.Find scalar product of vectors
 and
and
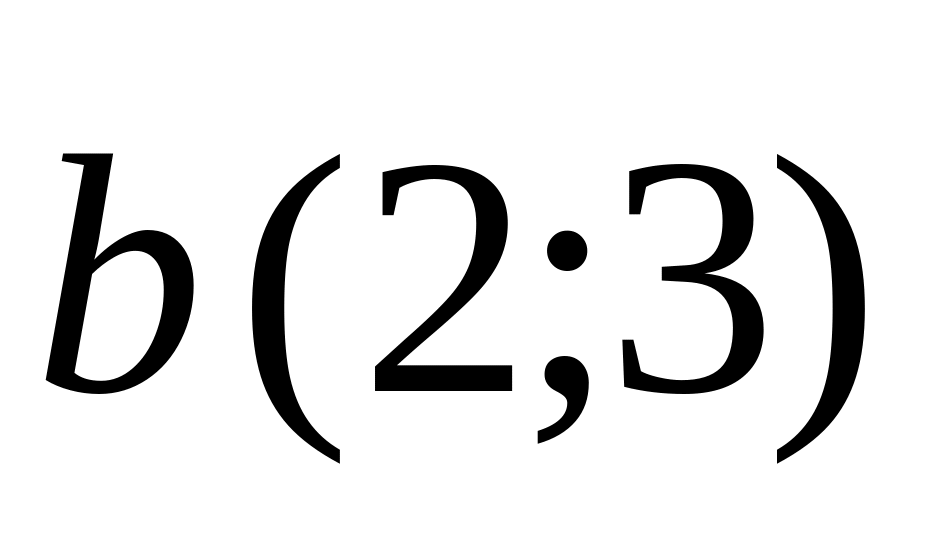 .
.Find an angle between vectors and
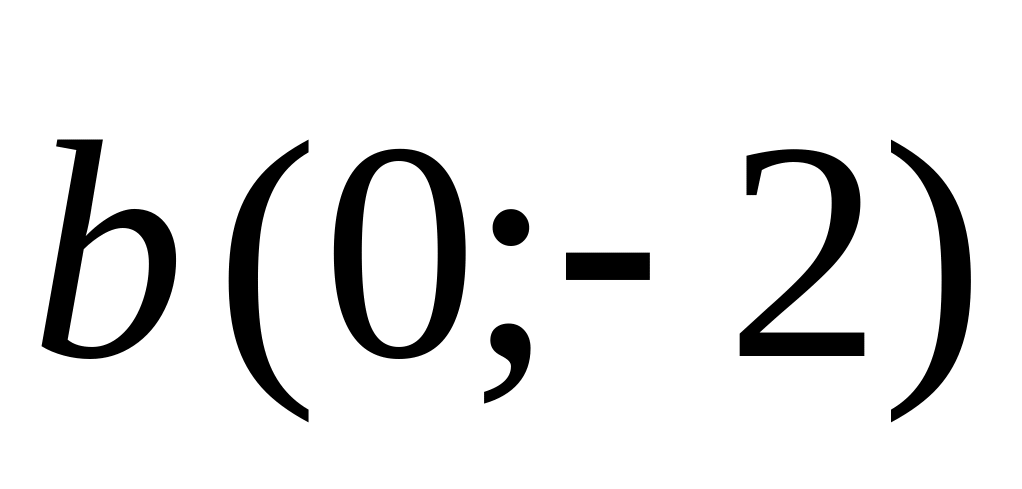 .
.At what value vectors
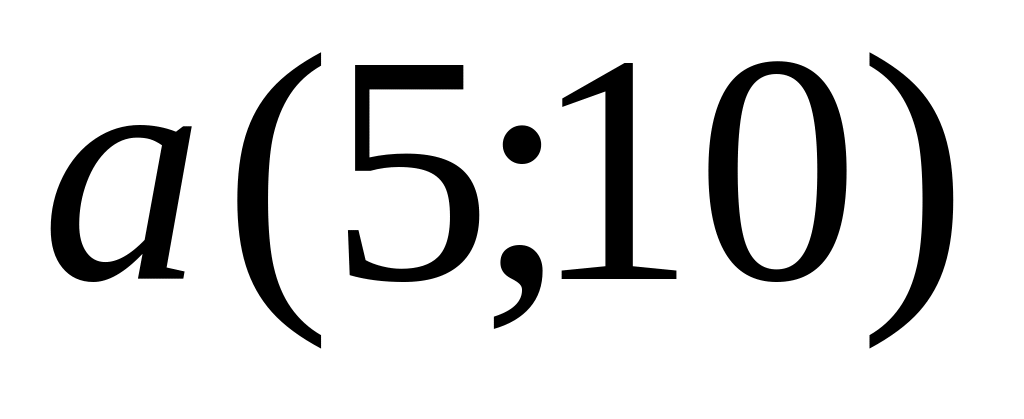 and
and
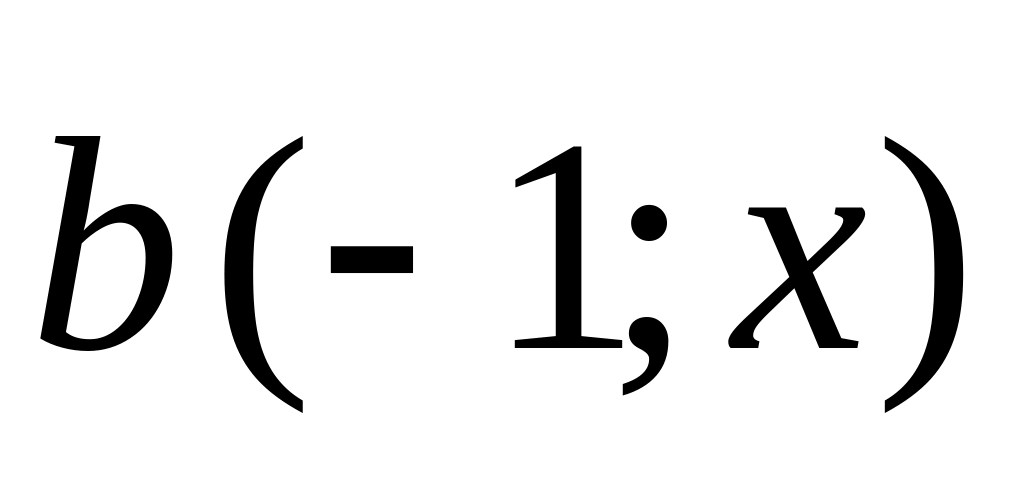 are
collinear to each other?
are
collinear to each other?At what value vectors and are orthogonal to each other?
An angle between vectors and is found by the formula:
Scalar product of vectors and is equal:
Scalar product of vectors and is equal to zero if:
Points
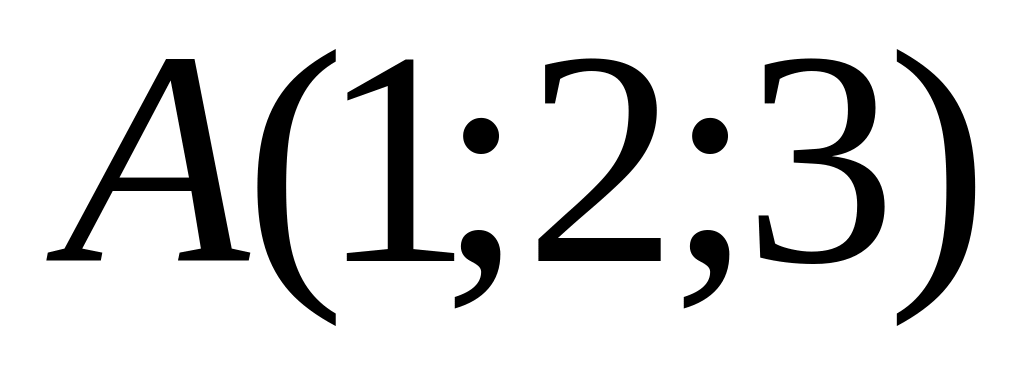 and
and
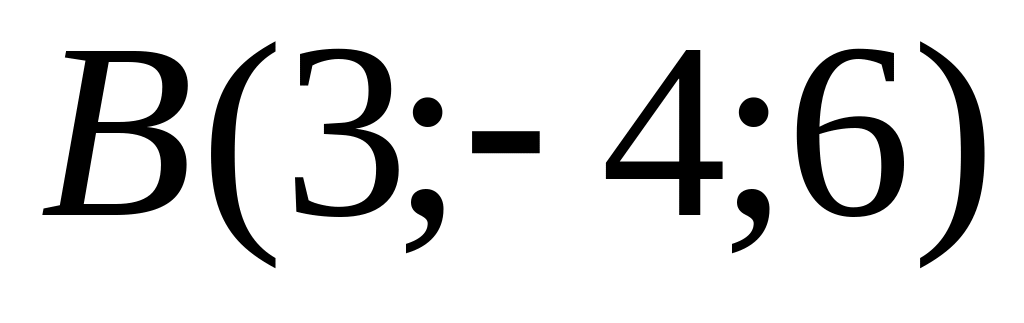 are given. Find length of a vector
.
are given. Find length of a vector
.Find , if
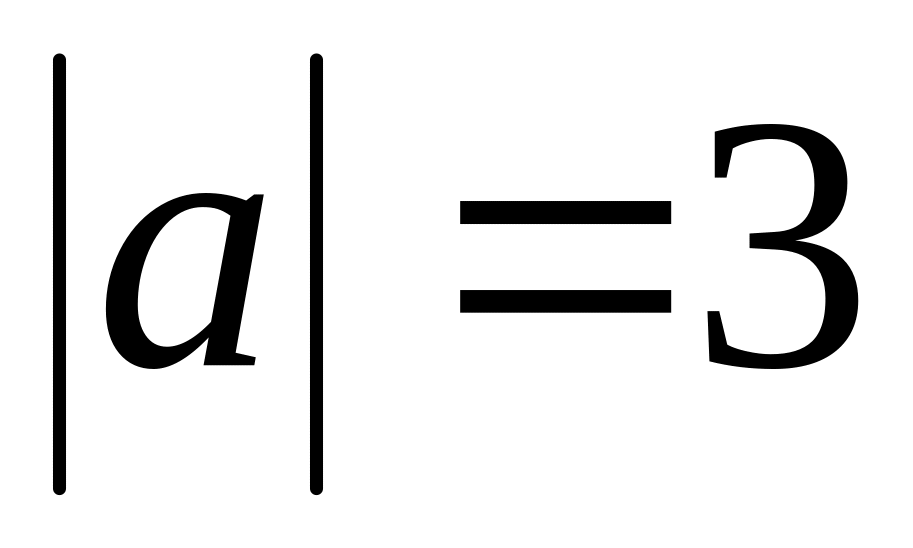 ,
,
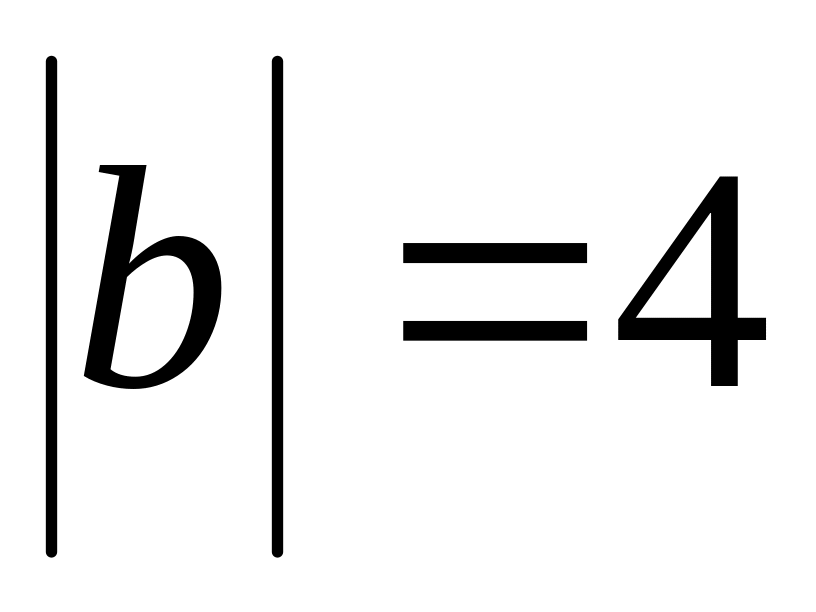 ,
,
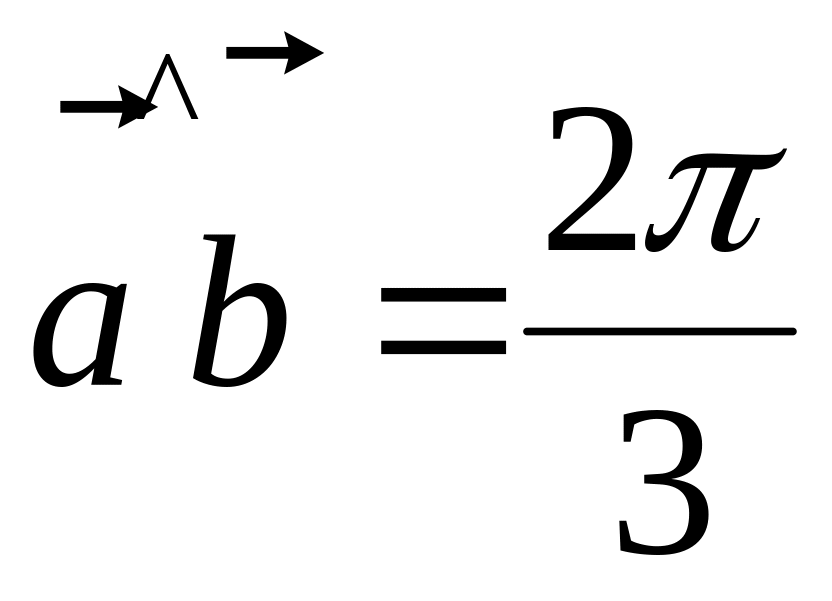 .
.Vectors are called equipollent, if they:
Find scalar product of vectors , if ,
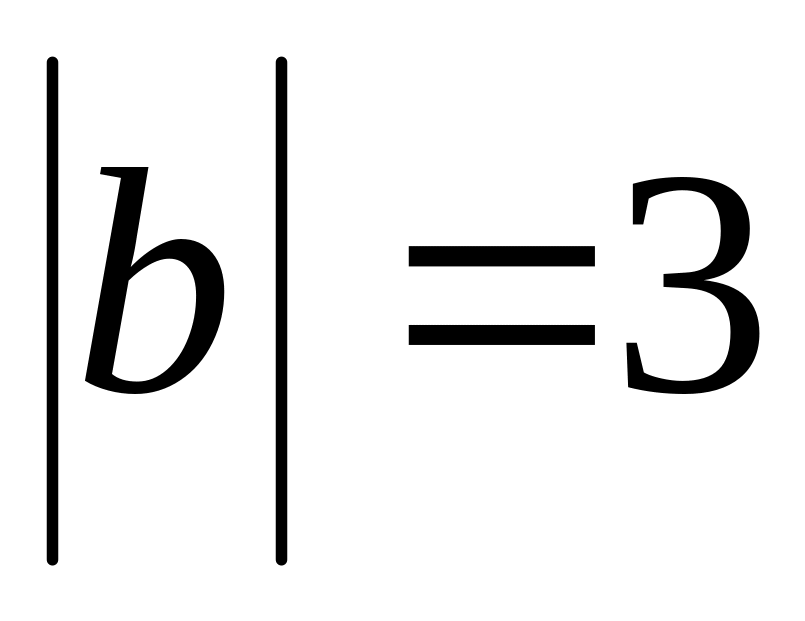 ,
,
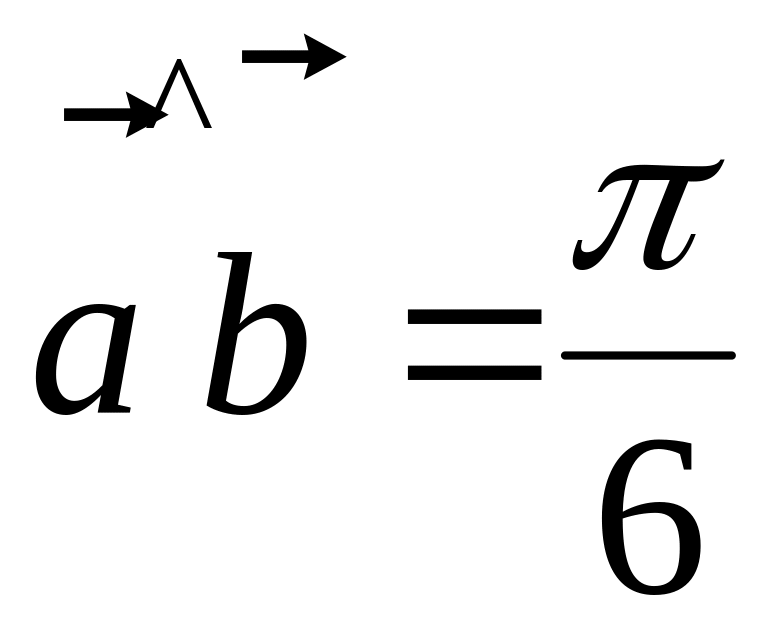 .
.Find
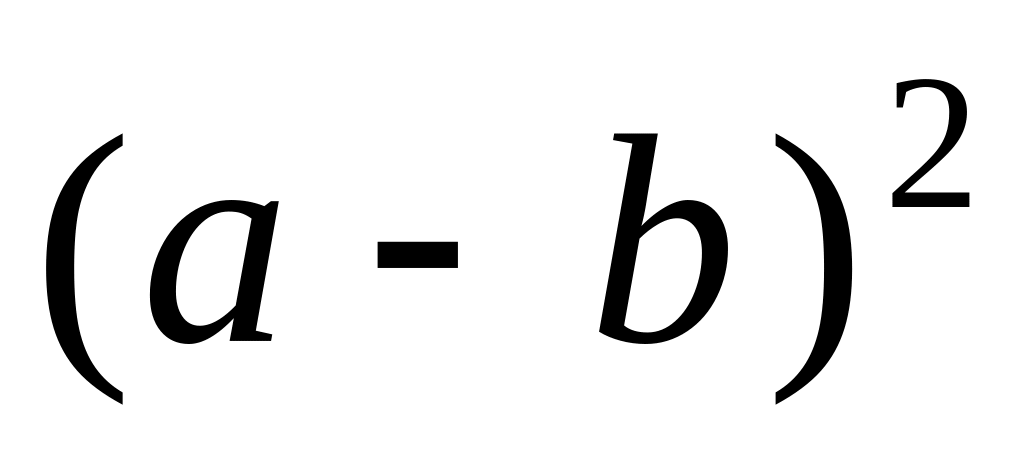 ,
if
,
if
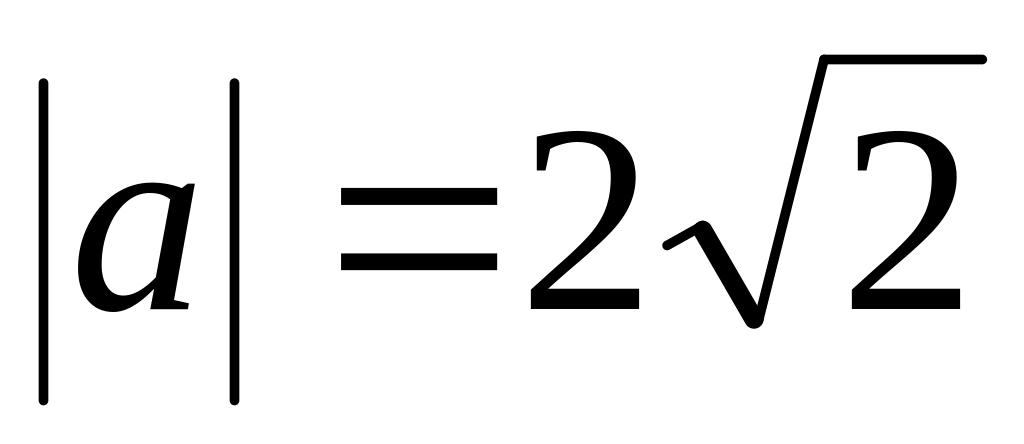 ,
,
,
,
 .
.Find
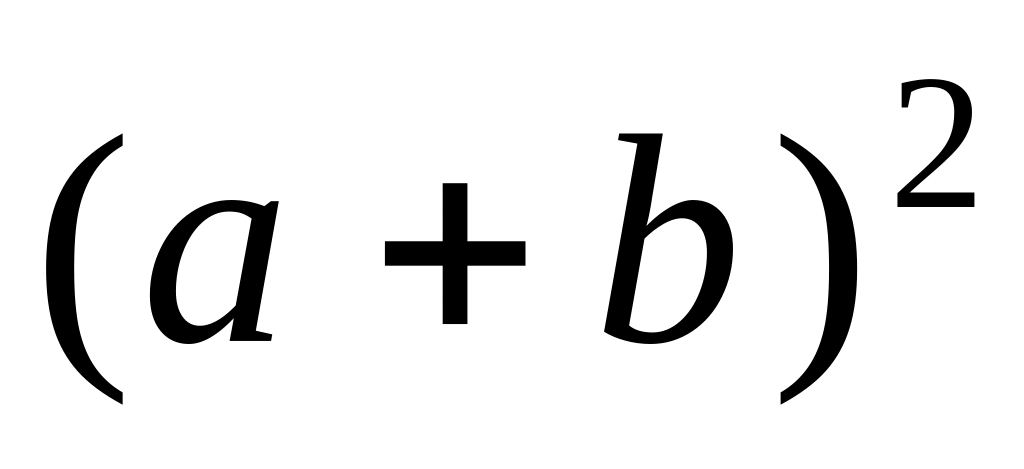 ,
if
,
,
.
,
if
,
,
.
Theme 4. The equation of a line on a plane and in space
Points
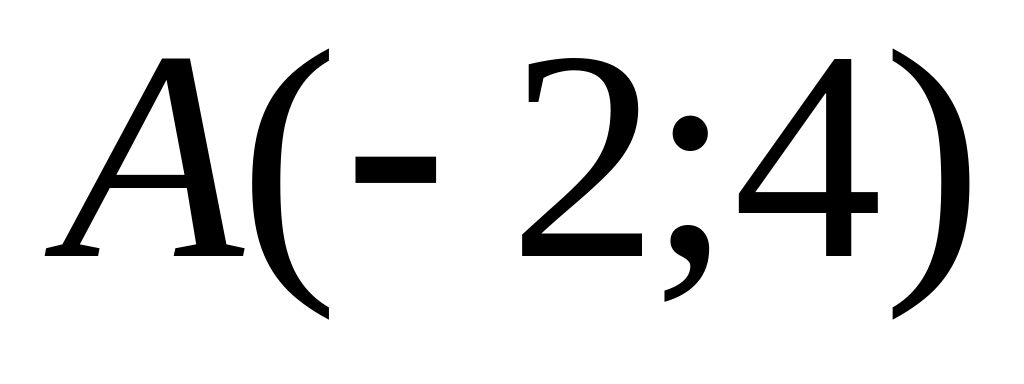 and
and
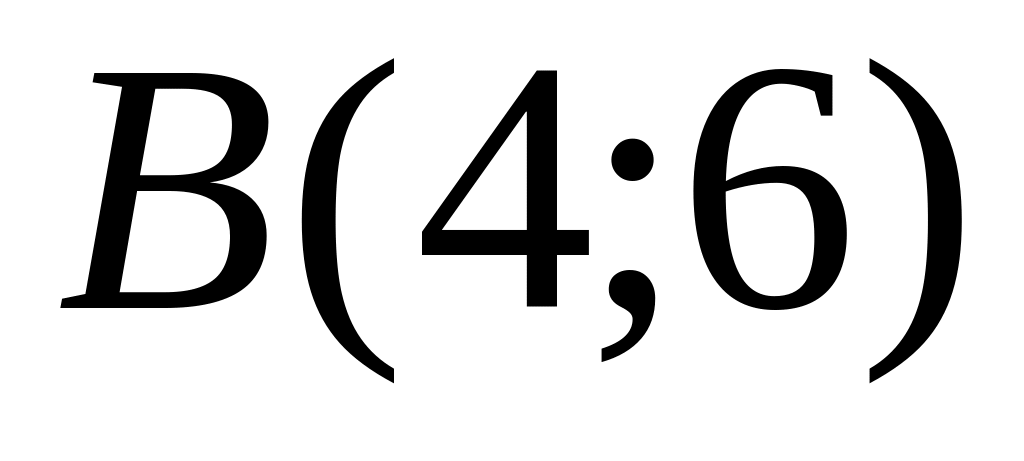 are given. Find coordinates of a midpoint
.
are given. Find coordinates of a midpoint
.In what point the straight line
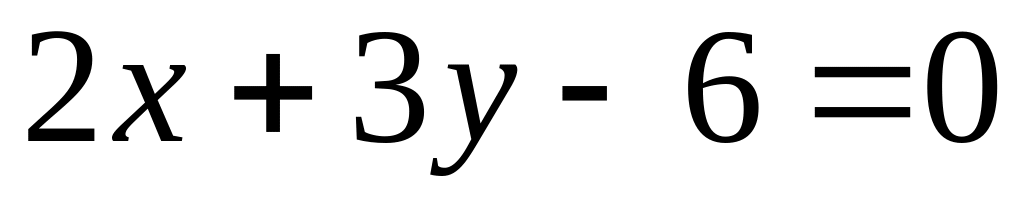 crosses
an axis
crosses
an axis
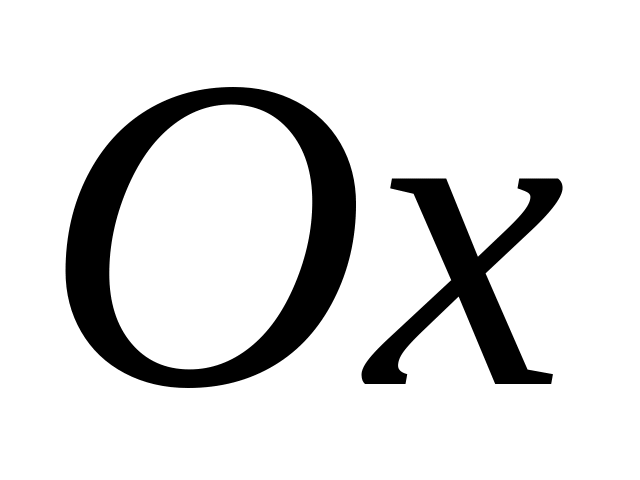 ?
?Find angular coefficient of a straight line, parallel straight line
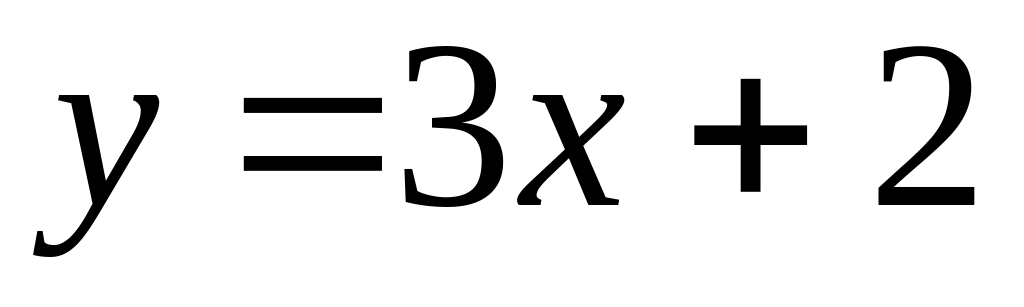 .
.Write down the equation of the straight line, which is passing through points
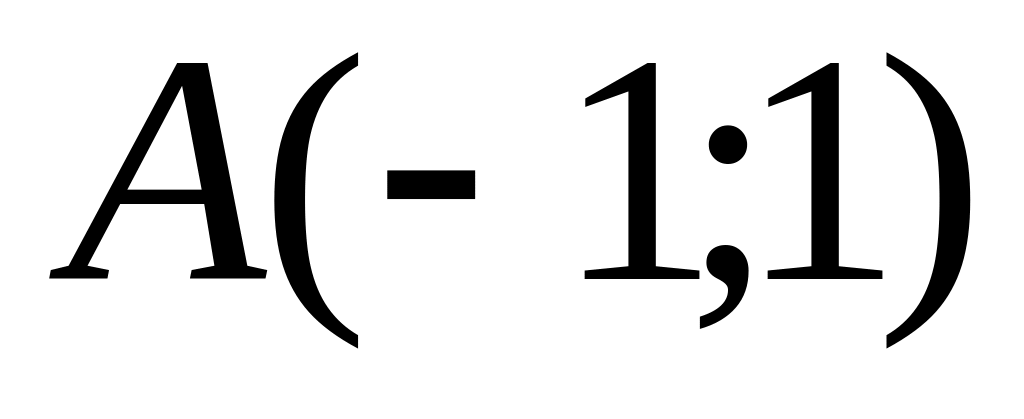 and
and
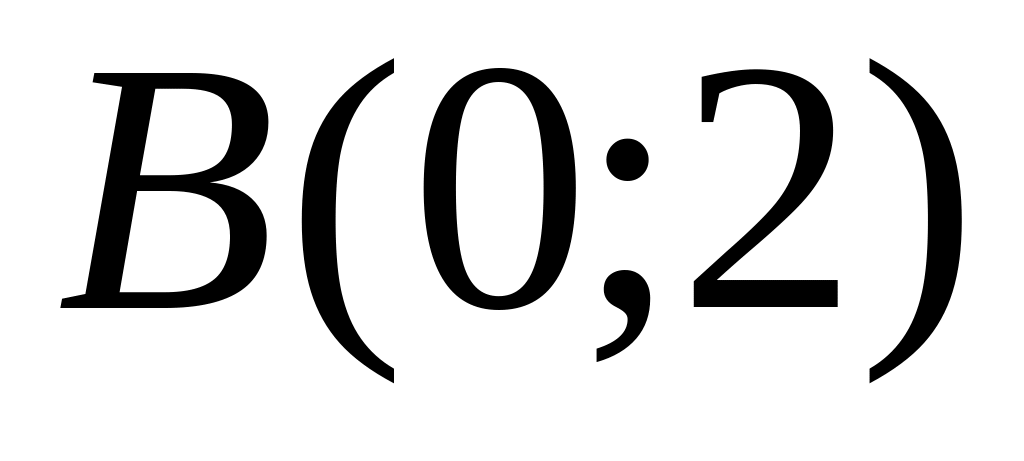 .
.Find the equation of a straight line on a plane in a general view.
Find the equation of a straight line with angular coefficient.
Points
 and
and
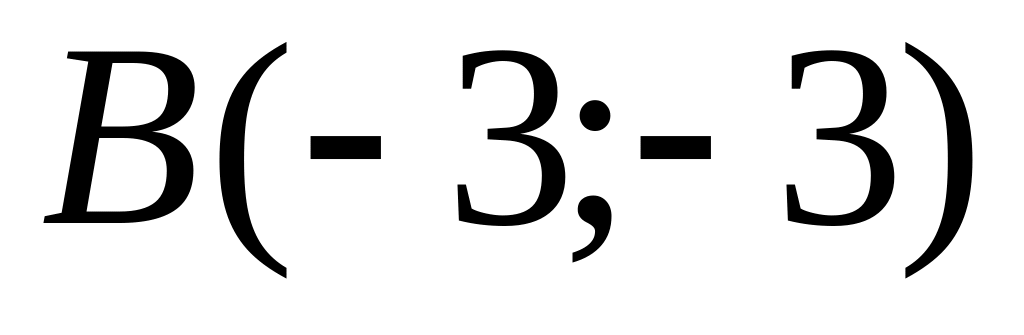 are given. Find coordinates of a midpoint
.
are given. Find coordinates of a midpoint
.In what point the straight line
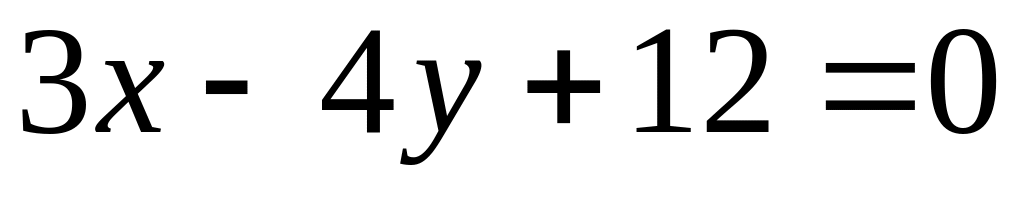 crosses an axis
crosses an axis
 ?
?Find angular coefficient of a straight line, parallel straight line
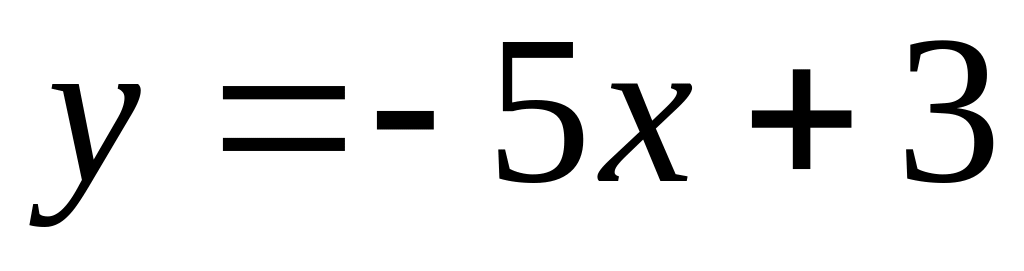 .
.Write down the equation of the straight line, which is passing through points
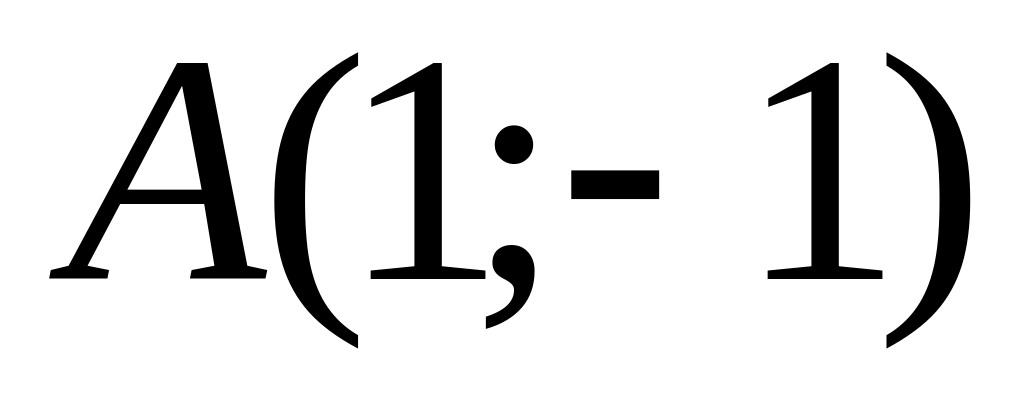 and
and
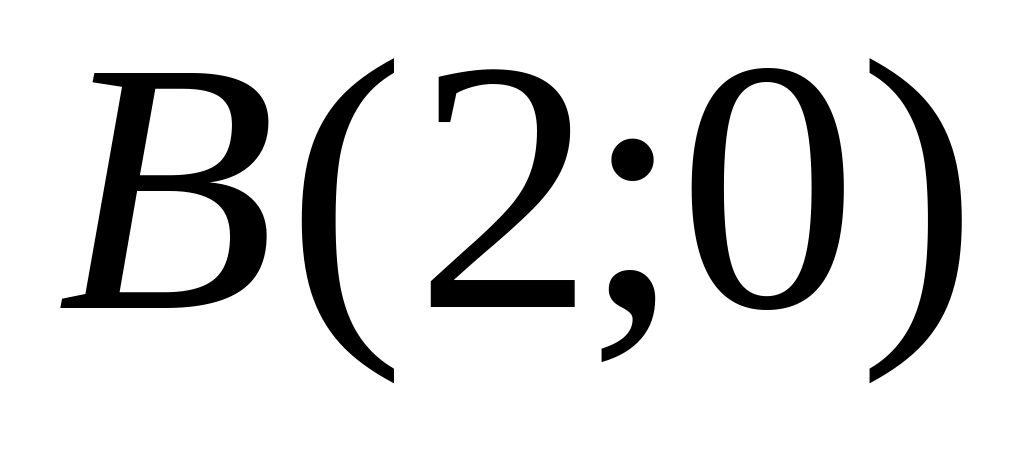 .
.Points
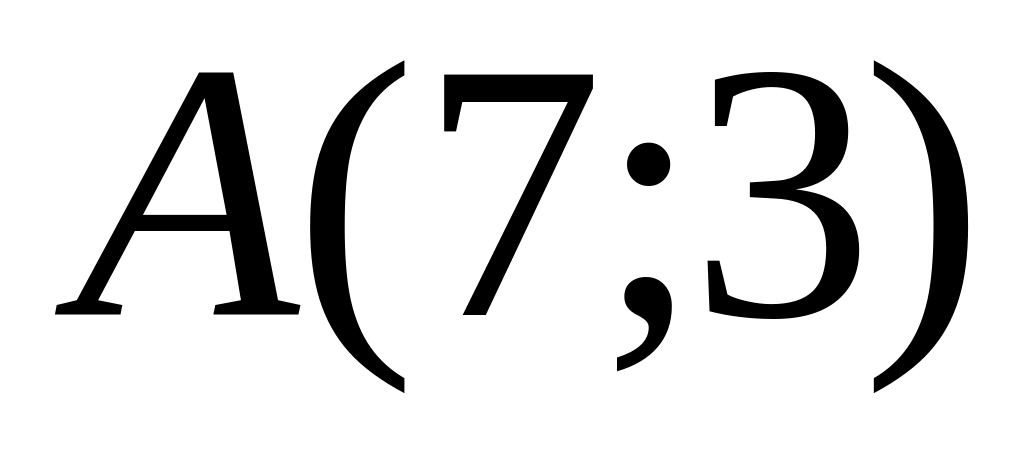 and
and
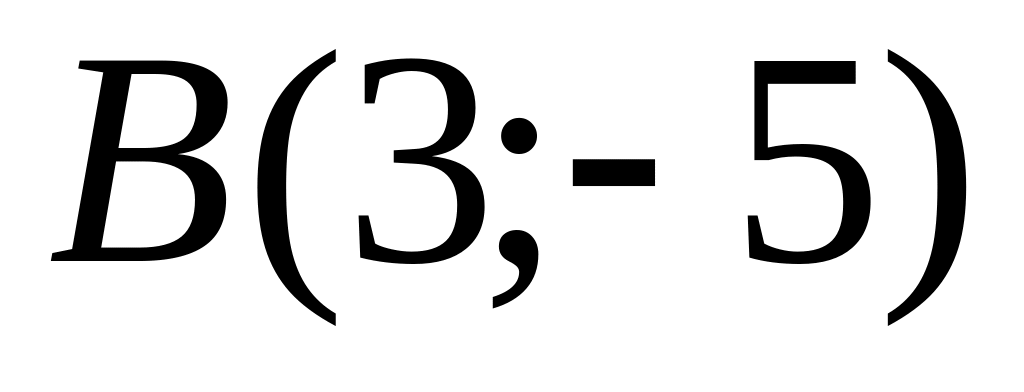 are given. Find coordinates of a midpoint
.
are given. Find coordinates of a midpoint
.In what point the straight line
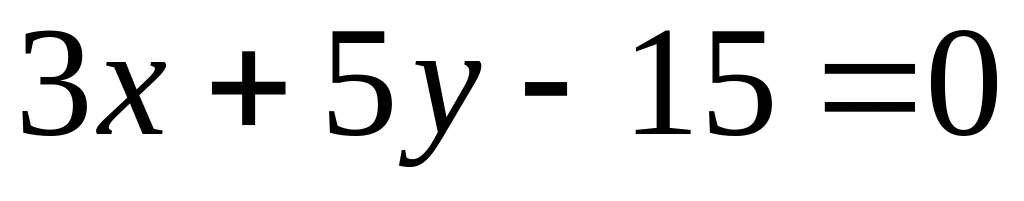 crosses an axis
?
crosses an axis
?Find angular coefficient of a straight line, parallel straight line
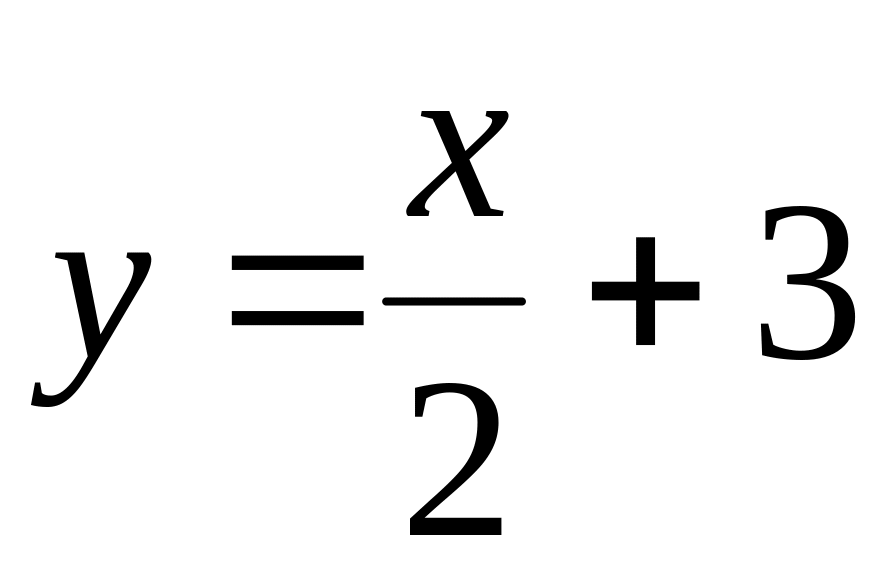 .
.Write down the equation of the straight line which is passing through points
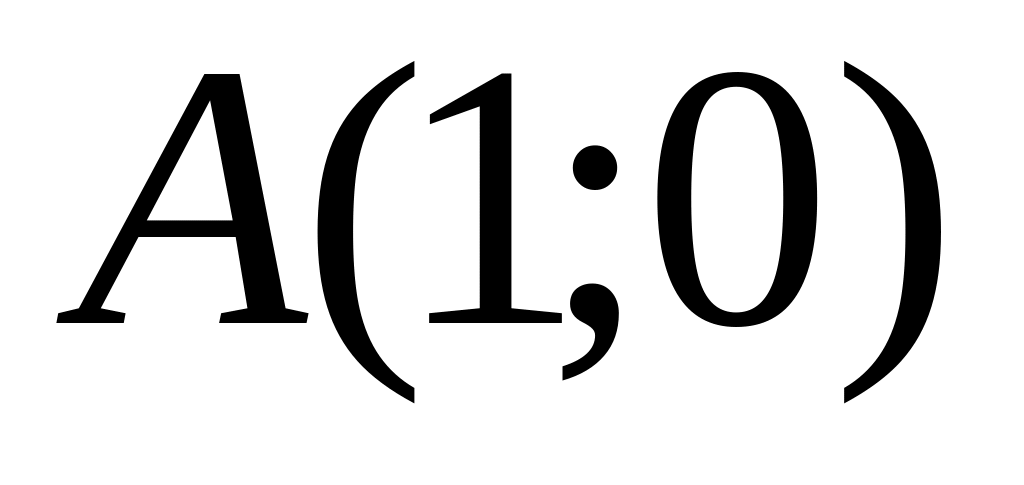 and
and
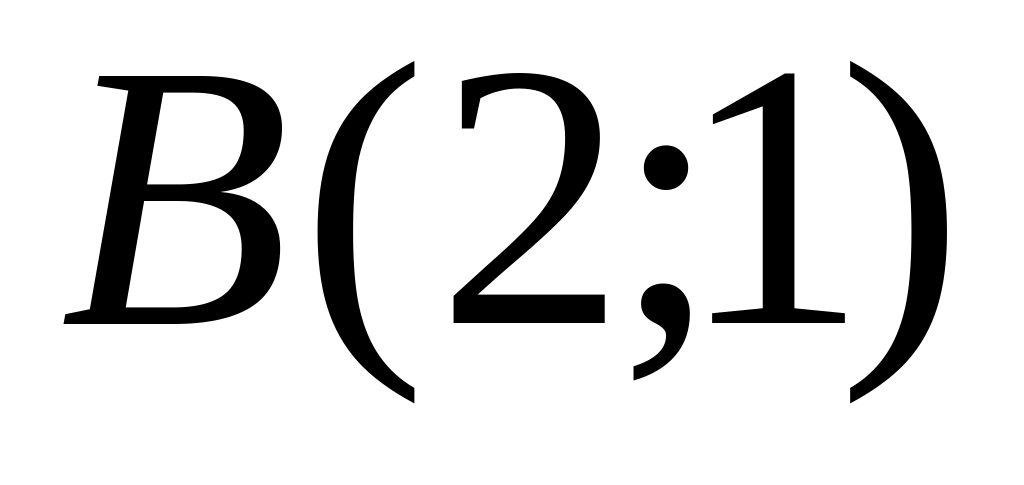 .
.Find the equation of the straight line, which is passing through points
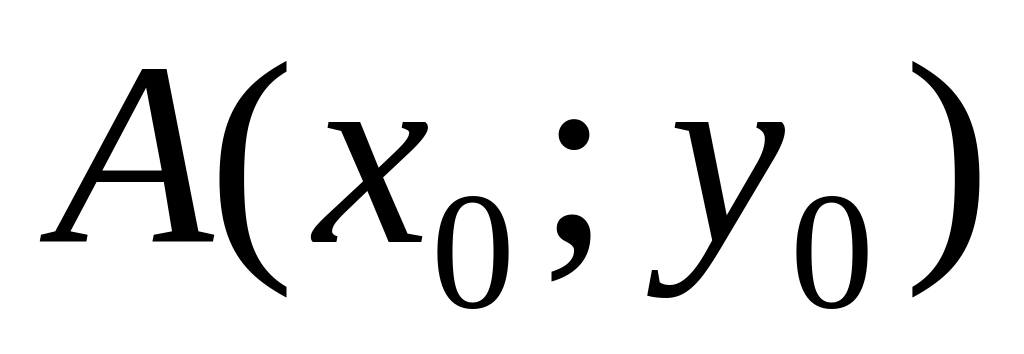 and
and
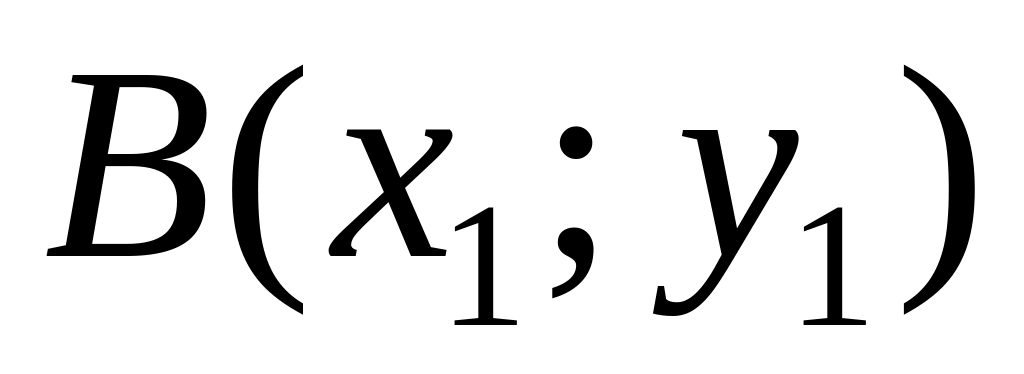 .
.Find the equation of an axis .
In what point the straight line
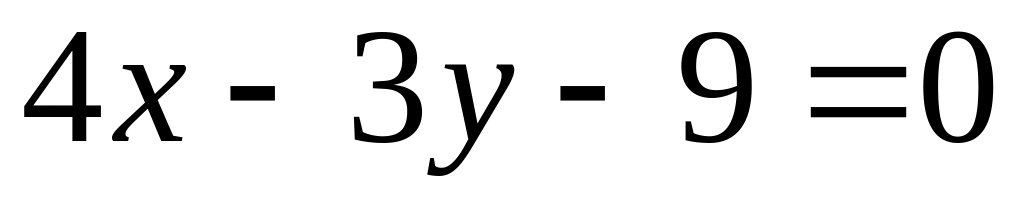 crosses an axis
?
crosses an axis
?Find angular coefficient of the straight line, parallel given straight line
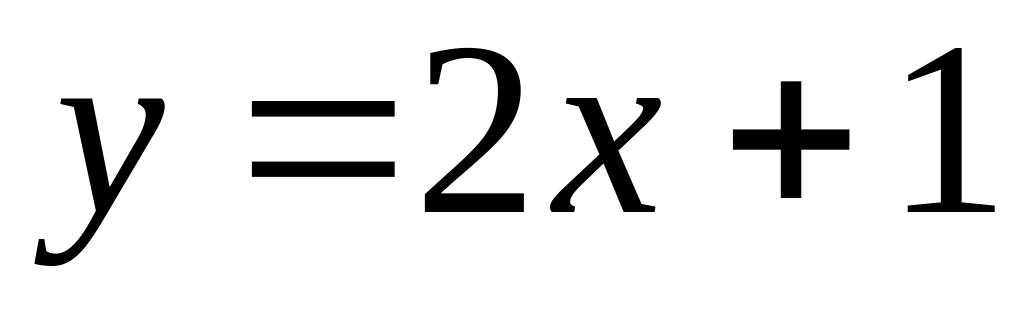 .
.Write down the equation of the straight line, which is passing through points
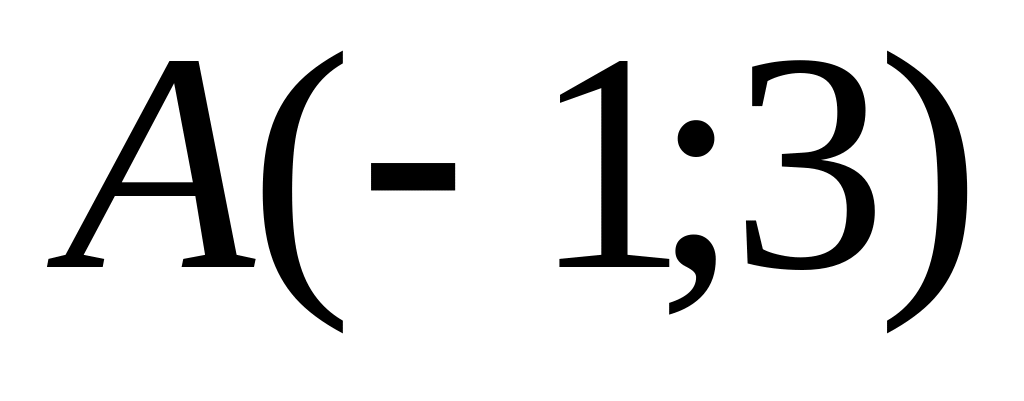 and
and
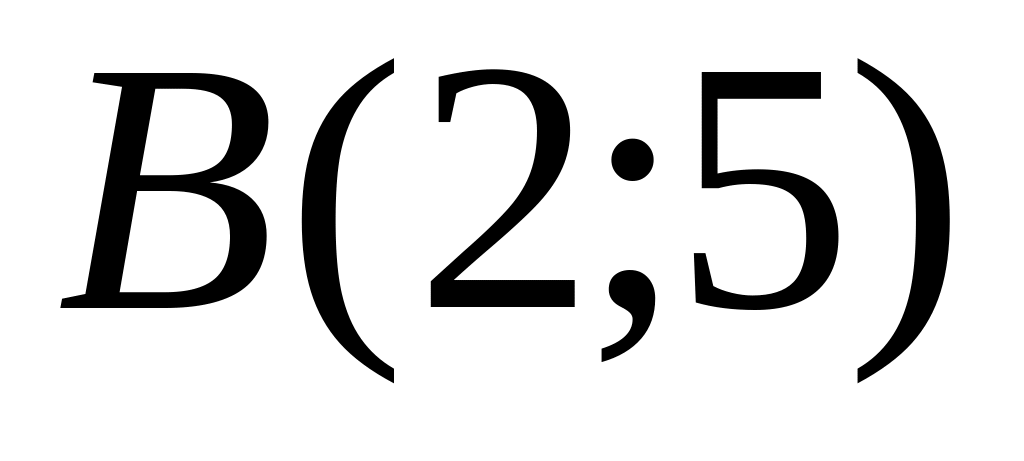 .
.Calculate distance from a point
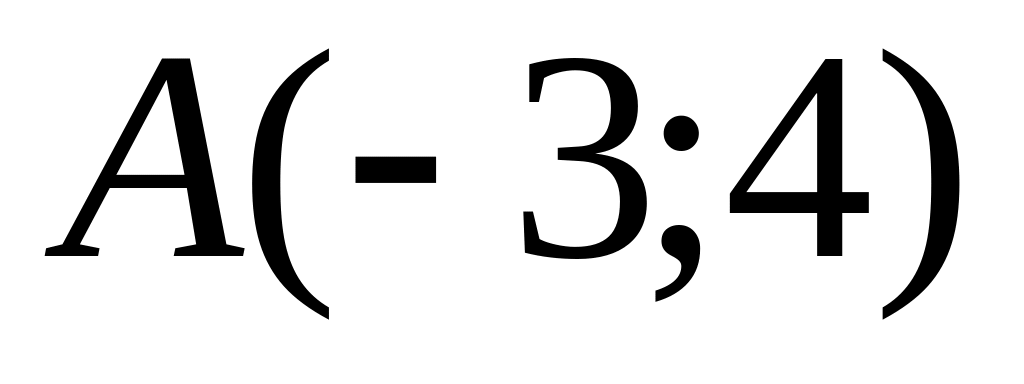 up
to a straight line
up
to a straight line
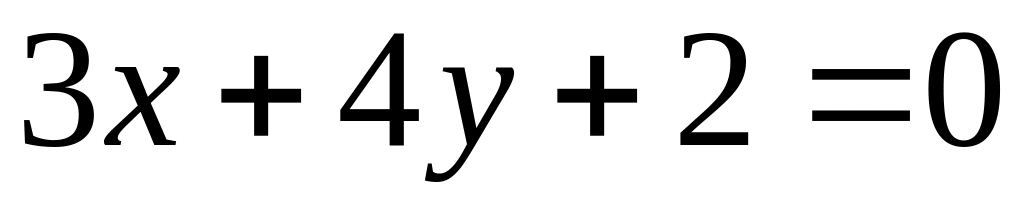 .
.Find the equation of a straight line on a plane in segments.
Find coordinates of a midpoint, connecting points
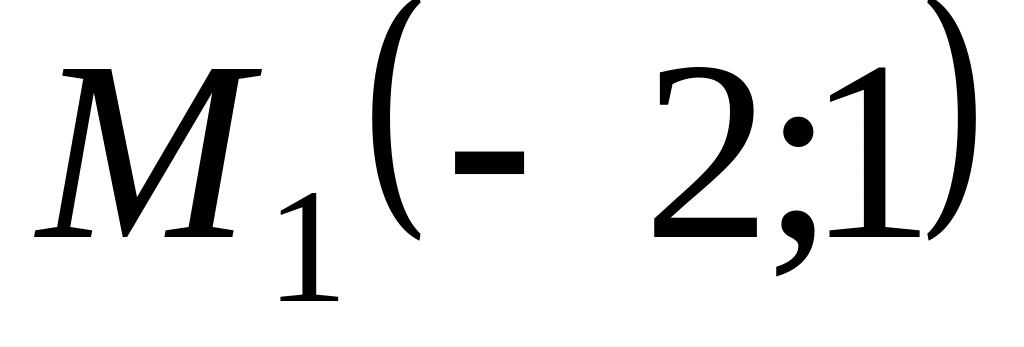 and
and
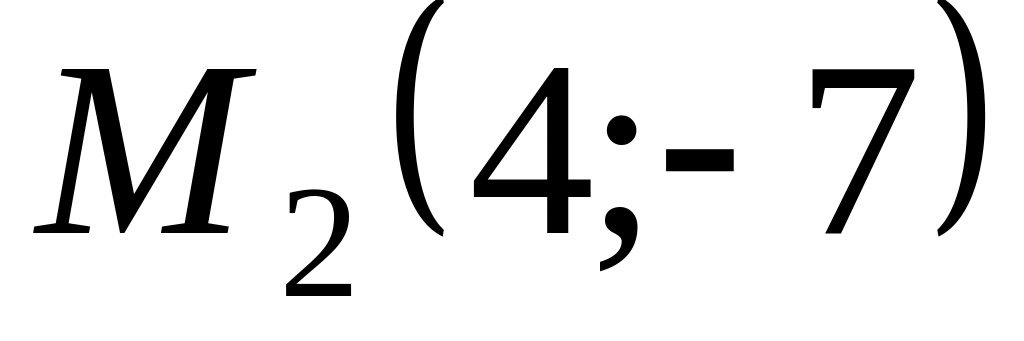 .
.Two straight lines
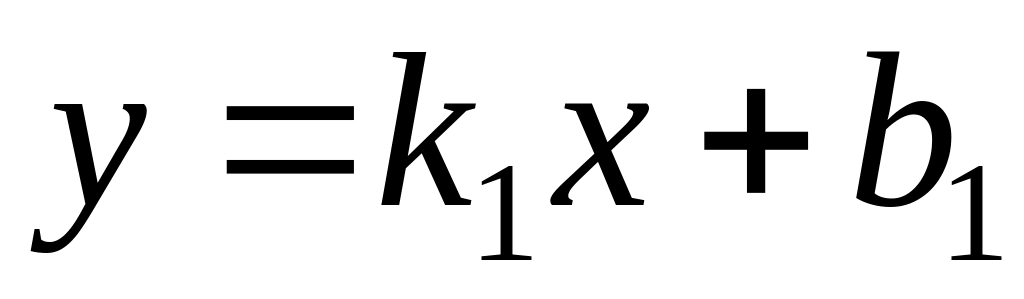 and
and
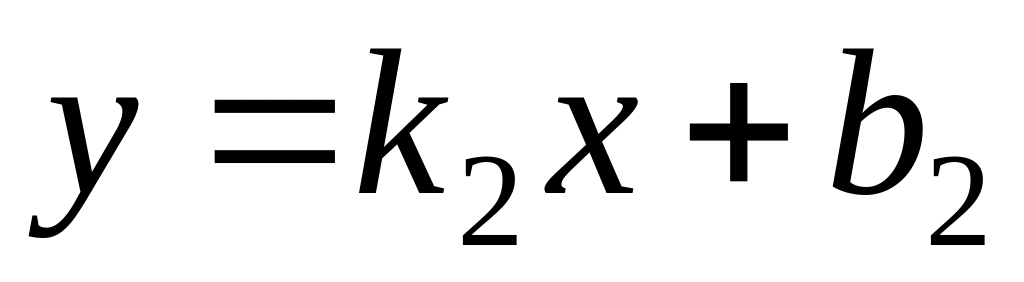 are parallel, if:
are parallel, if:Write the equation of a straight line with angular coefficient
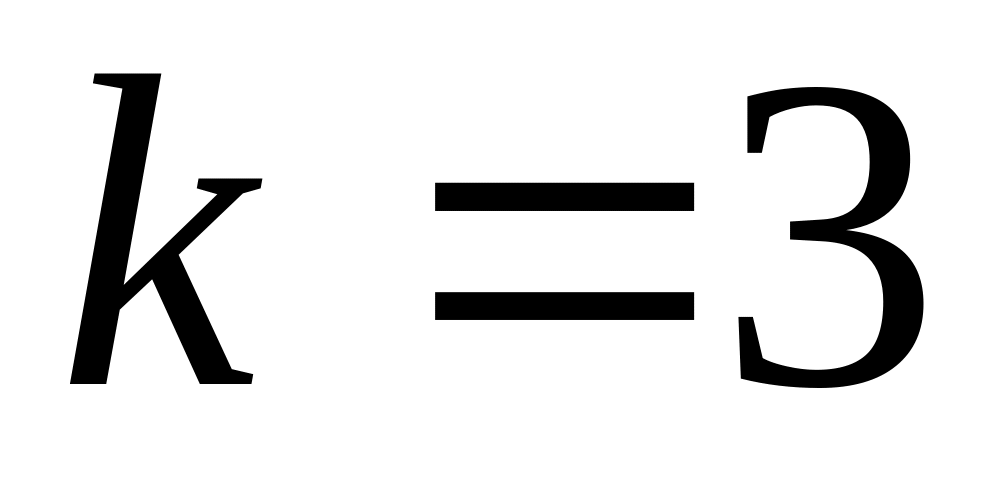 and passing through a point (2;-1).
and passing through a point (2;-1).Write the equation of the straight line, which is passing through points
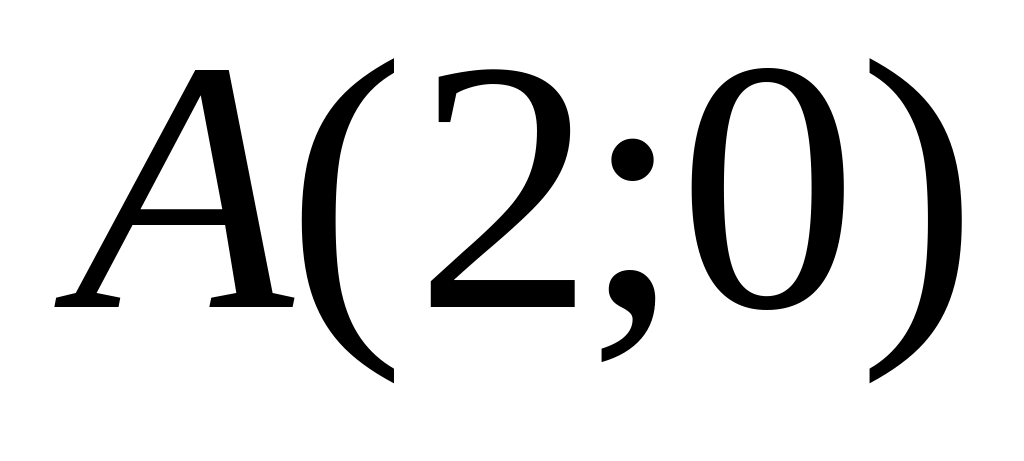 and
and
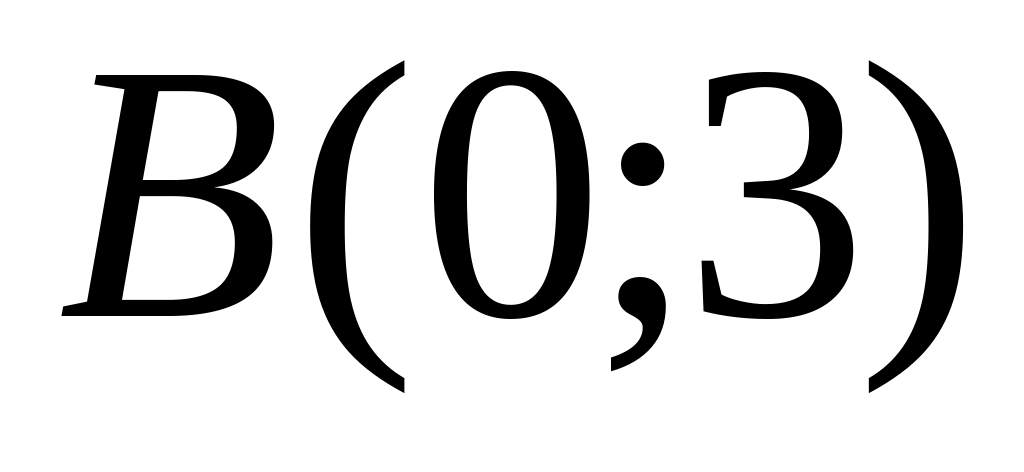 .
.Find a point of crossing of straight lines
 and
and
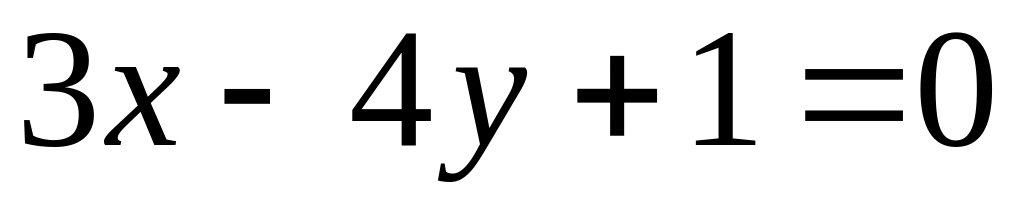 .
.Find the equation of a straight line in segments for a straight line
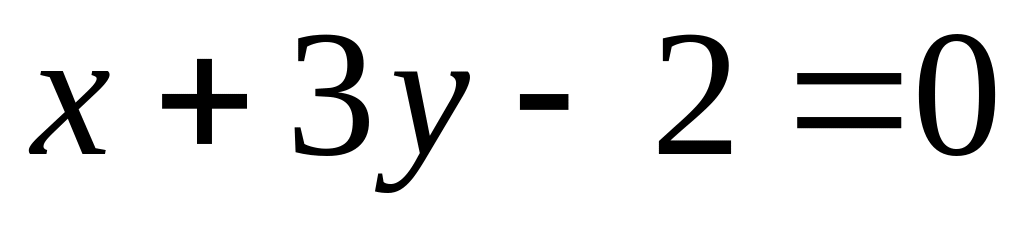 .
.Points
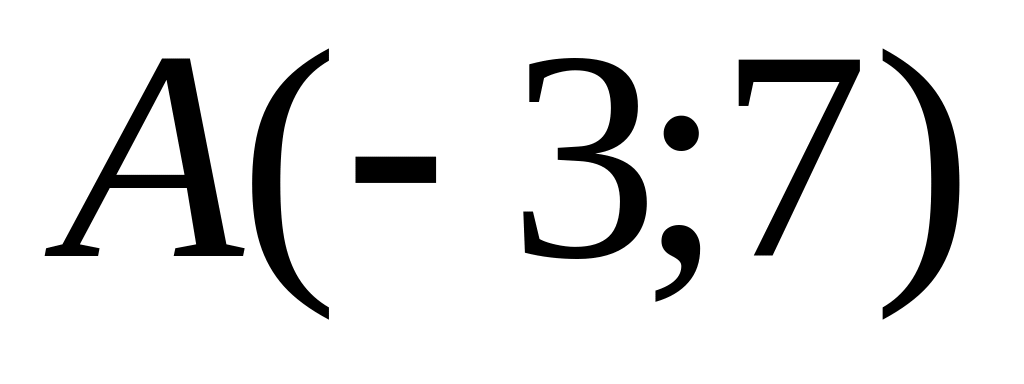 and
and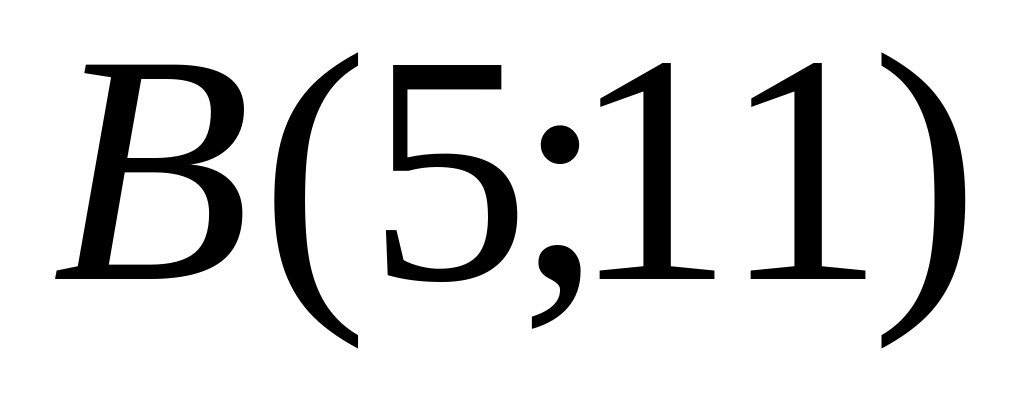 are given. Find coordinates of a midpoint
.
are given. Find coordinates of a midpoint
.Find distance between points
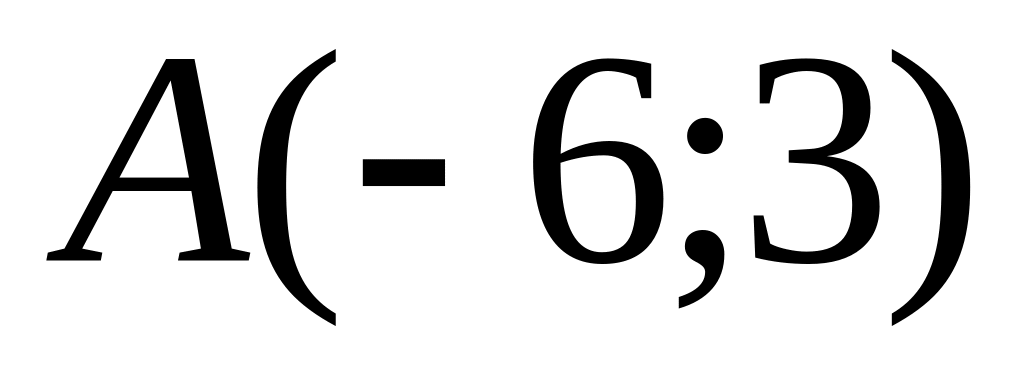 and
and
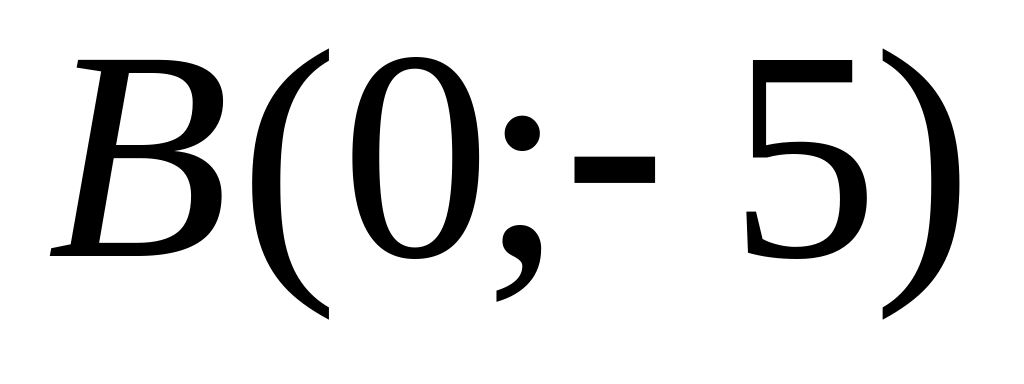 .
.Construct the equation of the straight line, which is passing through a point
 in parallel to the straight line
in parallel to the straight line
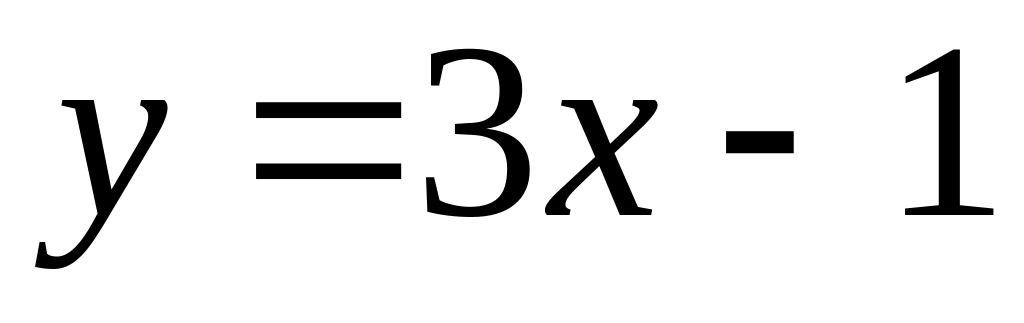 .
.Find a point of crossing of straight lines
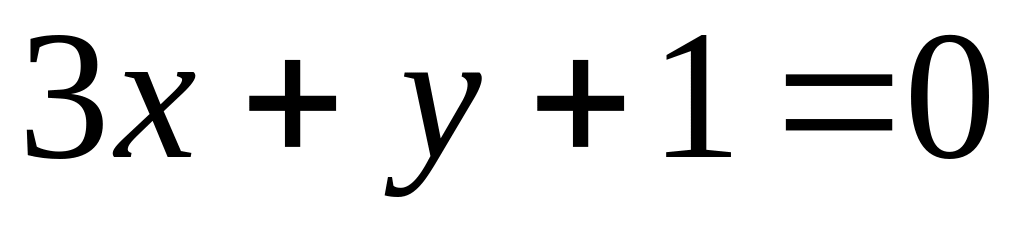 and
and
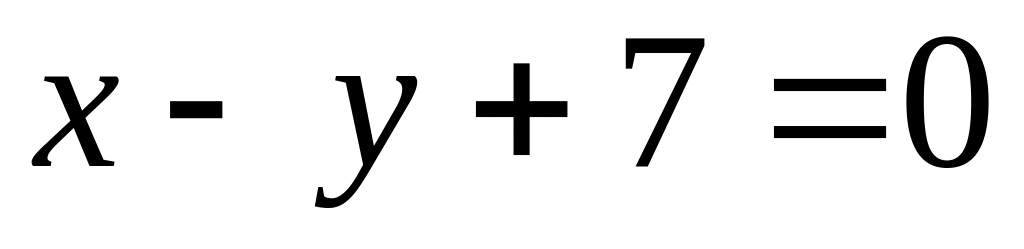 .
.Construct the equation of the straight line, which is passing through a point
 with
angular coefficient 4.
with
angular coefficient 4.Find a point of crossing of straight lines
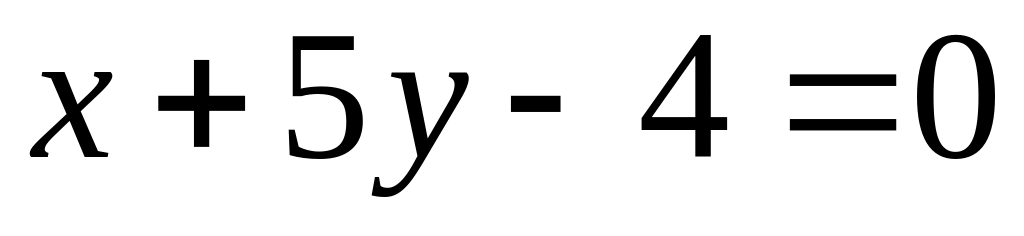 and
and
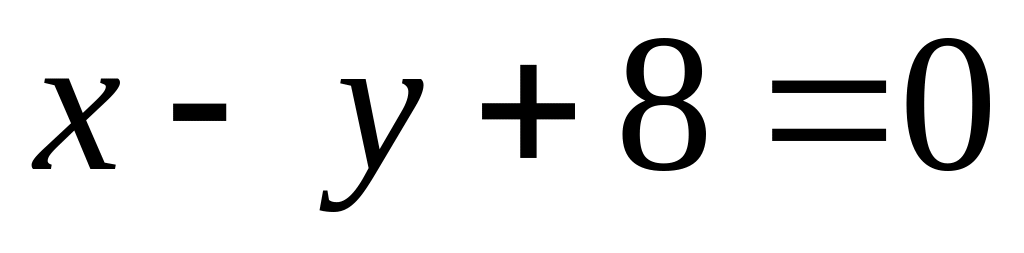 .
.Find the equation of the straight line, which is passing through points
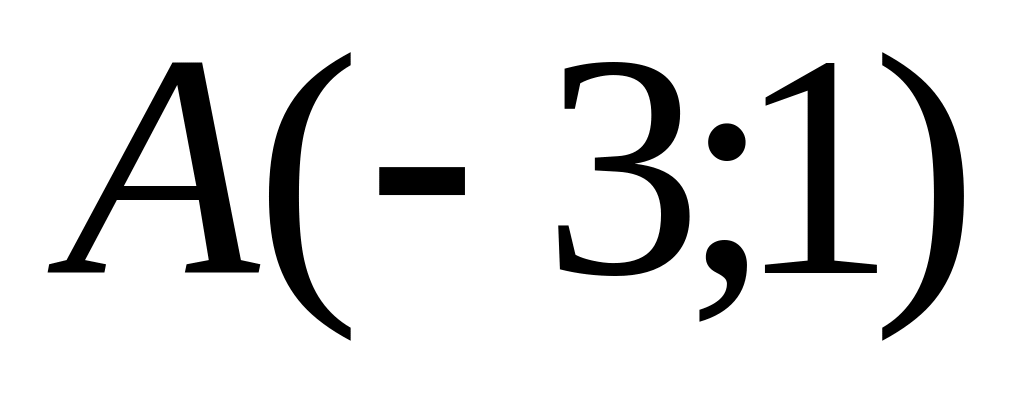 and
and
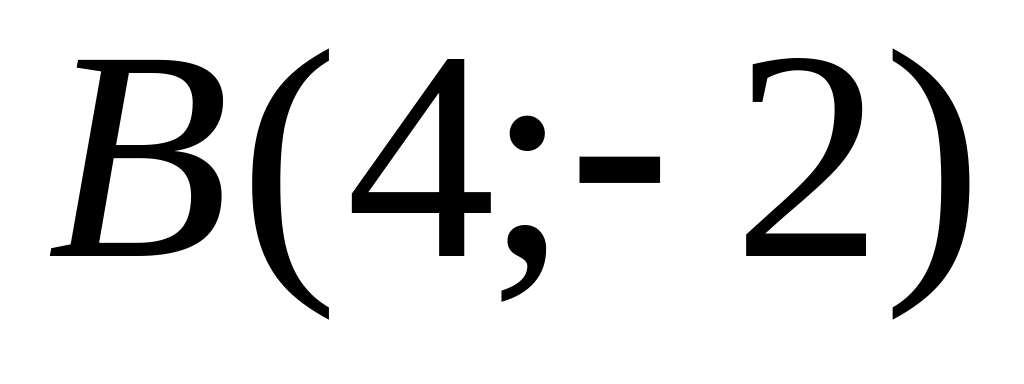 .
.Find a condition of parallelism of straight lines
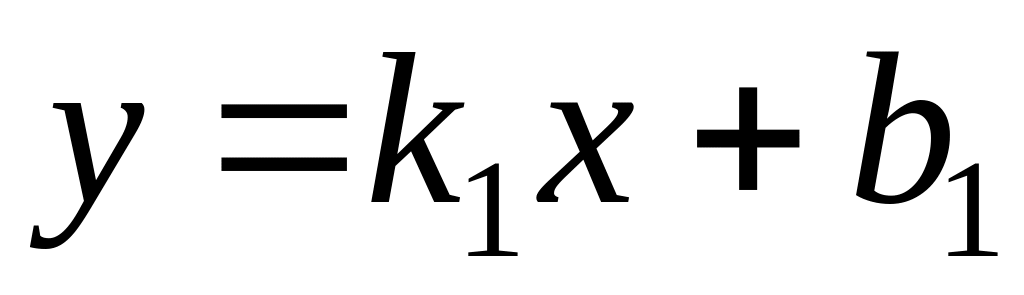 and
and
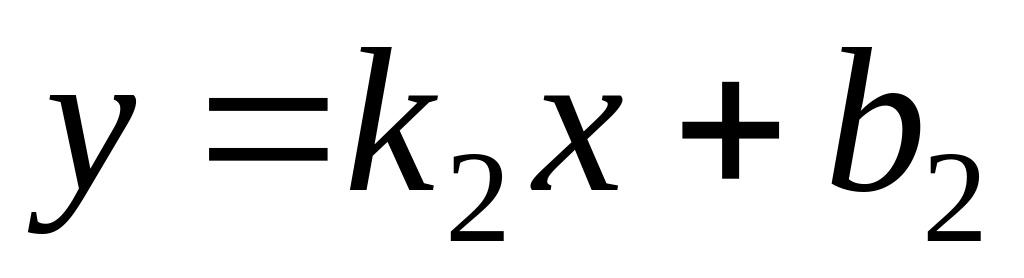 .
.Find a condition of perpendicularity of straight lines and .
Equation of a straight line with angular coefficient is given by:
Find the equation of the straight line, which is passing through points and .
Find the equation of the straight line, which is passing through a point
 ,
in parallel a vector
,
in parallel a vector
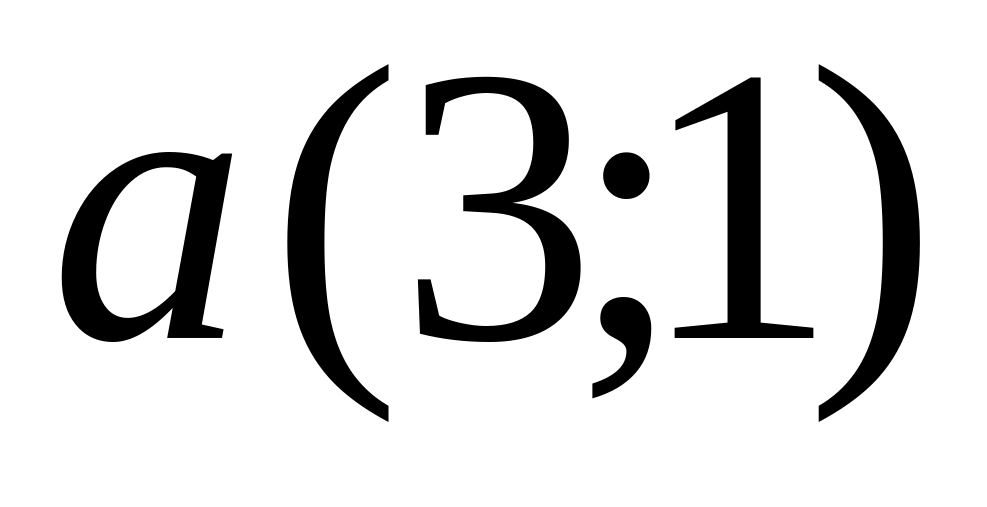 .
.If
 - an angle between straight lines
and
- an angle between straight lines
and
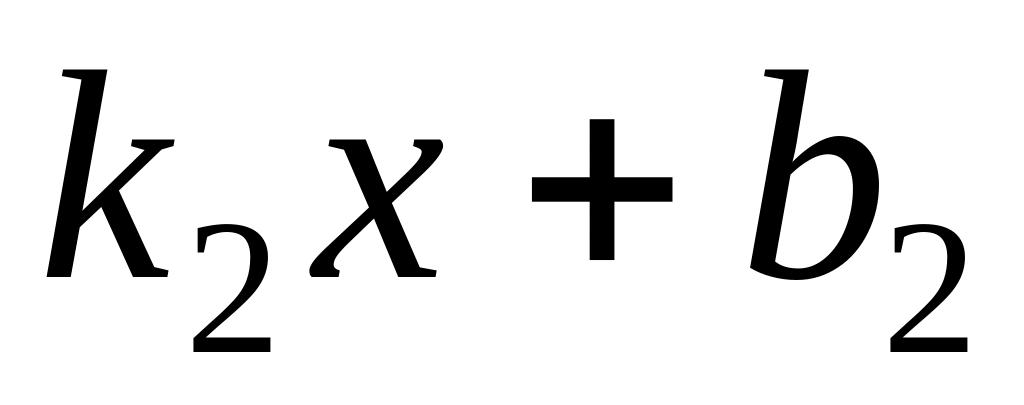 ,
what of following parameters expression
,
what of following parameters expression
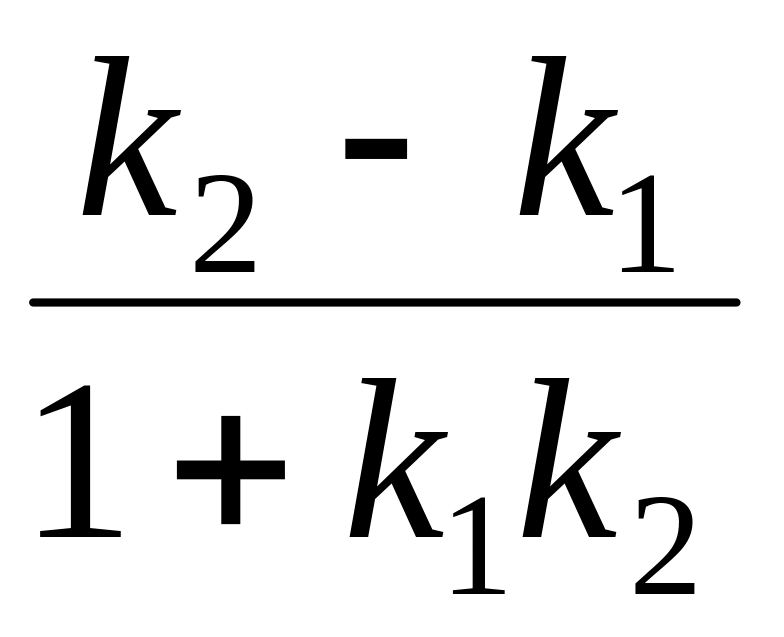 defines?
defines?Find distance from a point
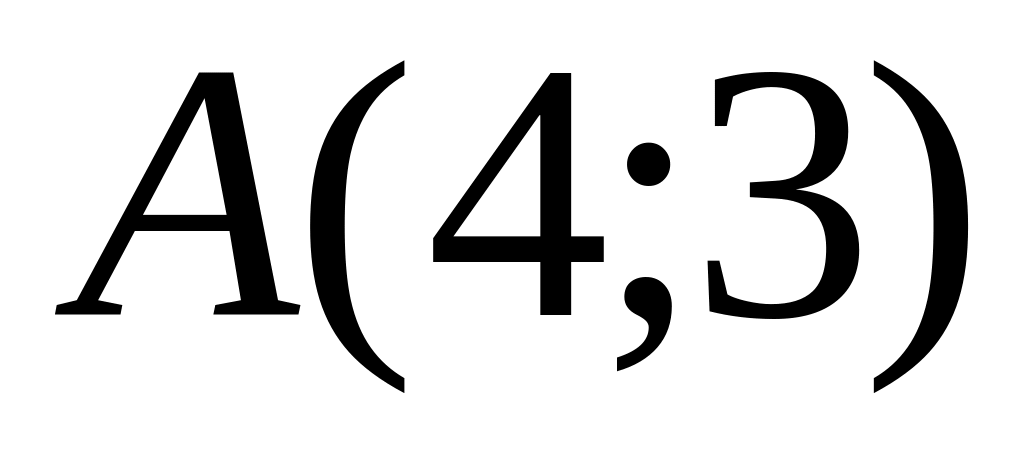 up to a straight line
up to a straight line
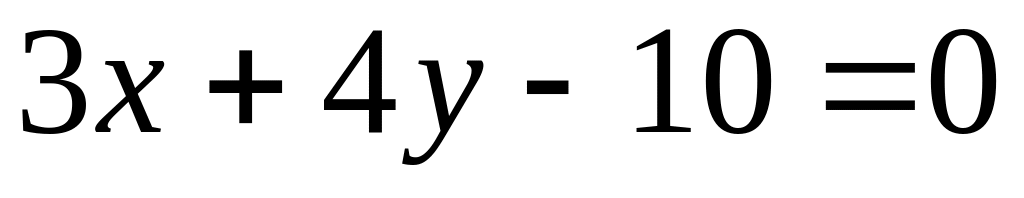 .
.Find an angle between straight lines
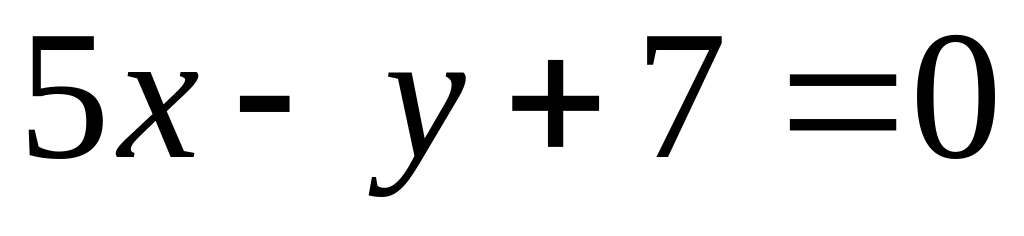 and
and
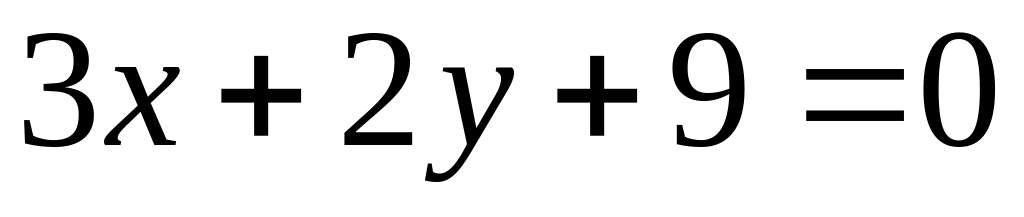 .
.Find angular coefficient of a straight line, perpendicular straight line
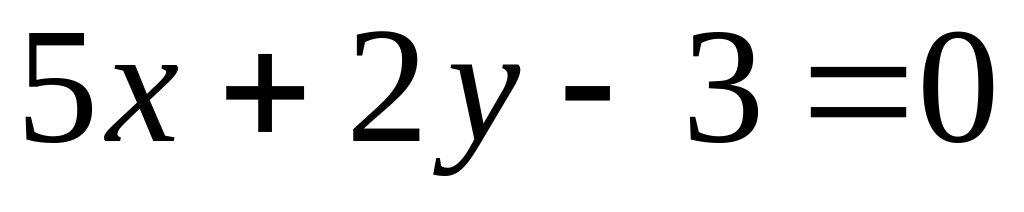 .
.Find the equation of the straight line, which is passing through a point
 and a parallel straight line
and a parallel straight line
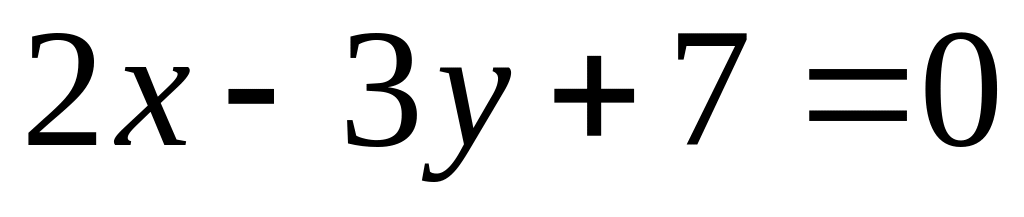 .
.Construct the equation of the straight line, which is passing through a point
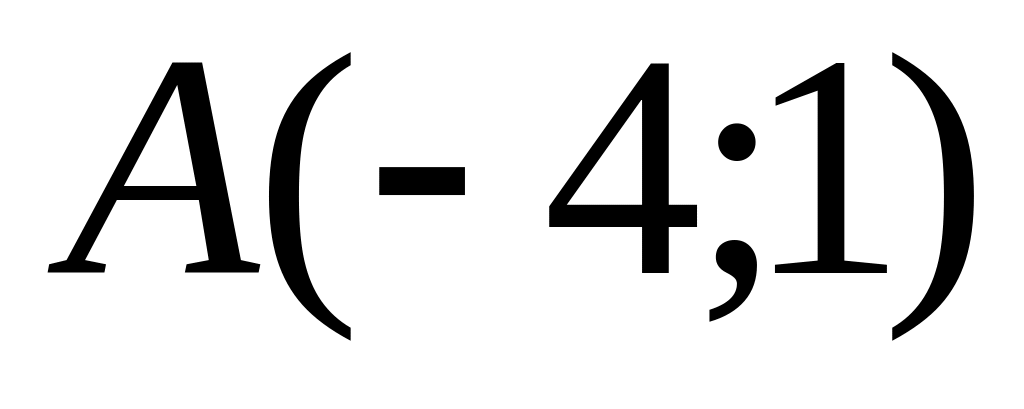 in parallel axes
.
in parallel axes
.
Theme 5. Function. Limits and a continuity
Find a limit
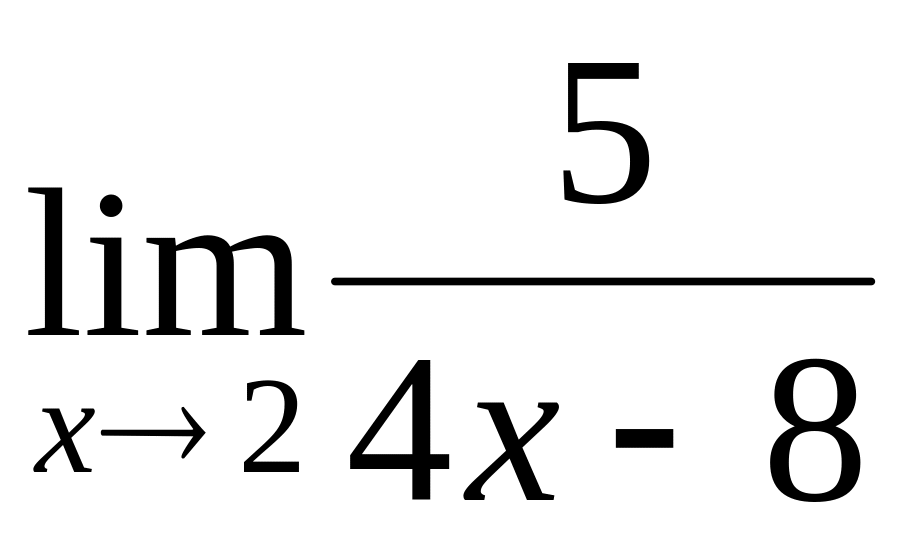 .
.Find a limit
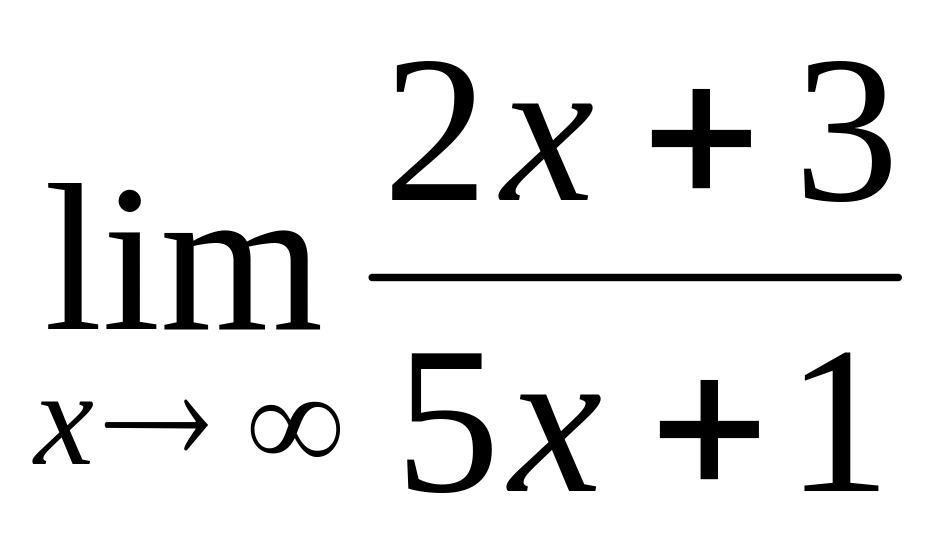 .
.Find a limit
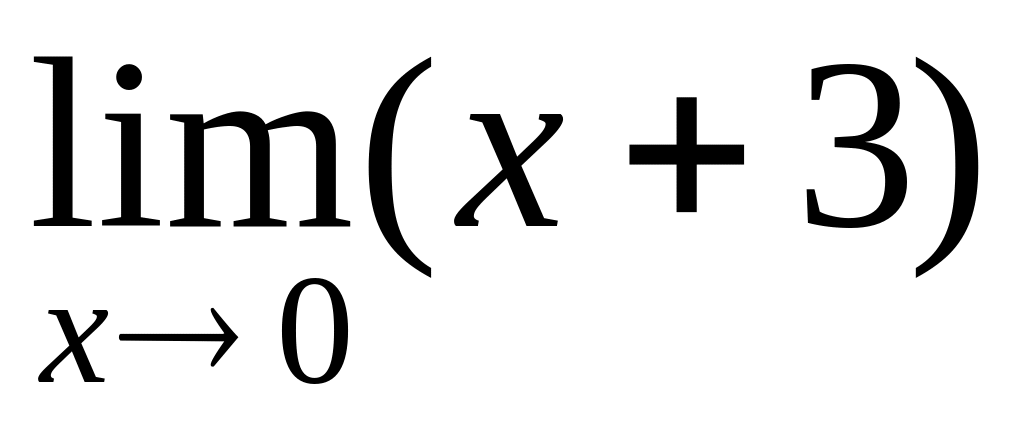 .
.Find a limit
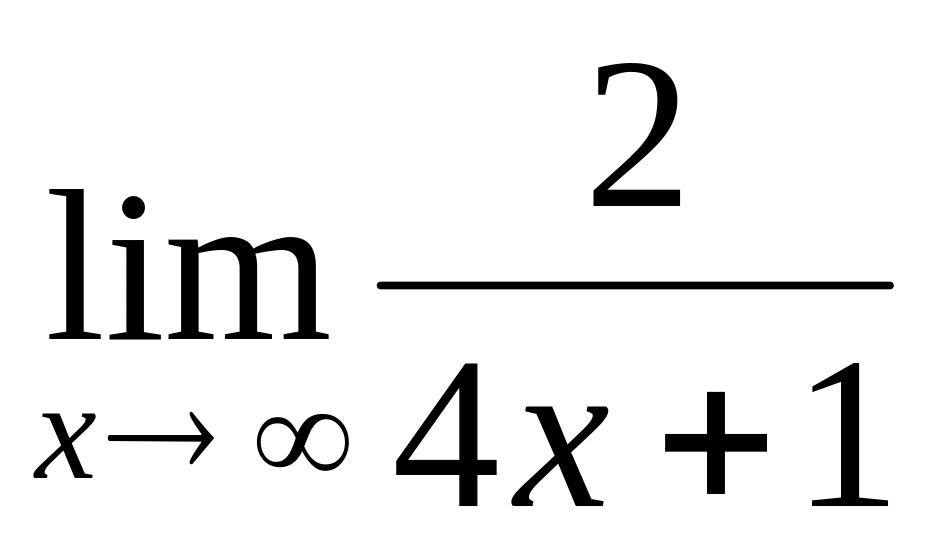 .
.Find a limit
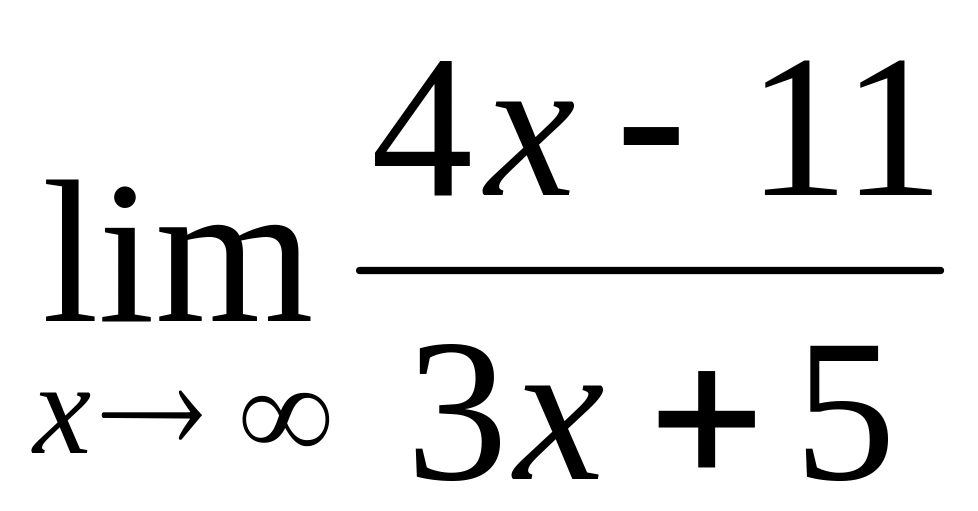 .
.Find a limit
 .
.Find a limit
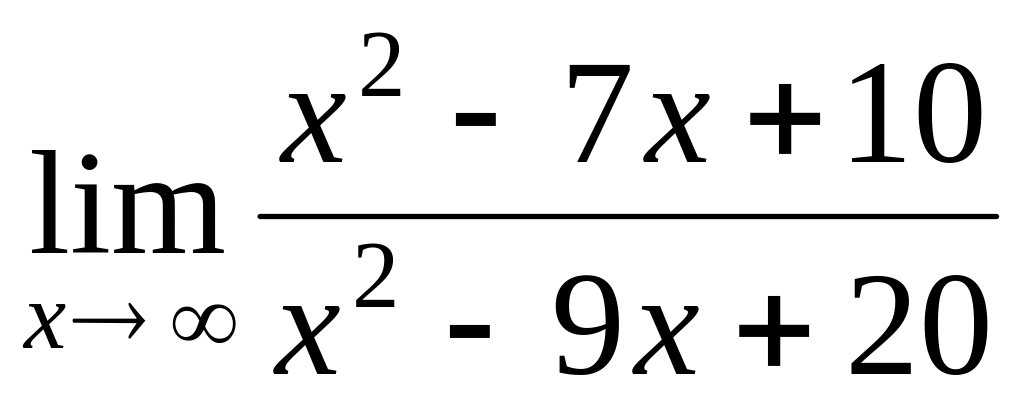 .
.Find a limit
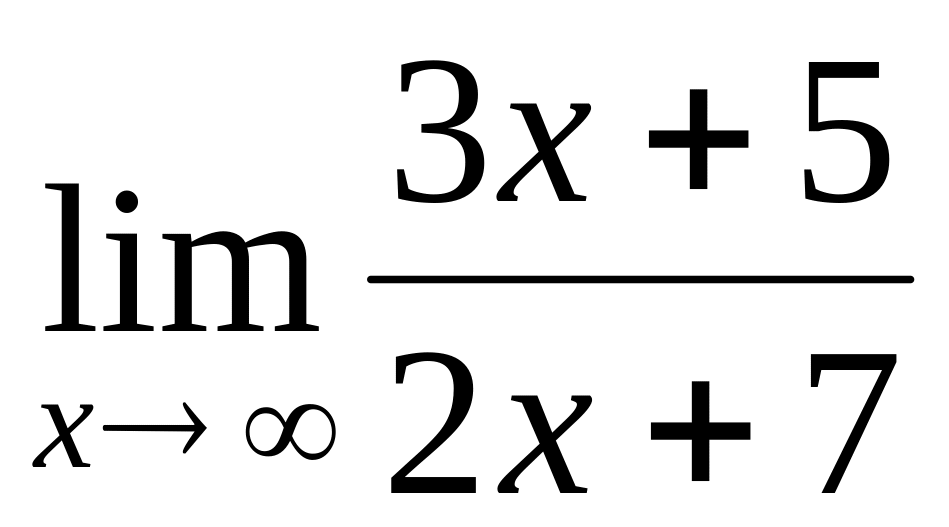 .
.Сalculate a limit
 by means of Lhopital rule.
by means of Lhopital rule.Сalculate a limit
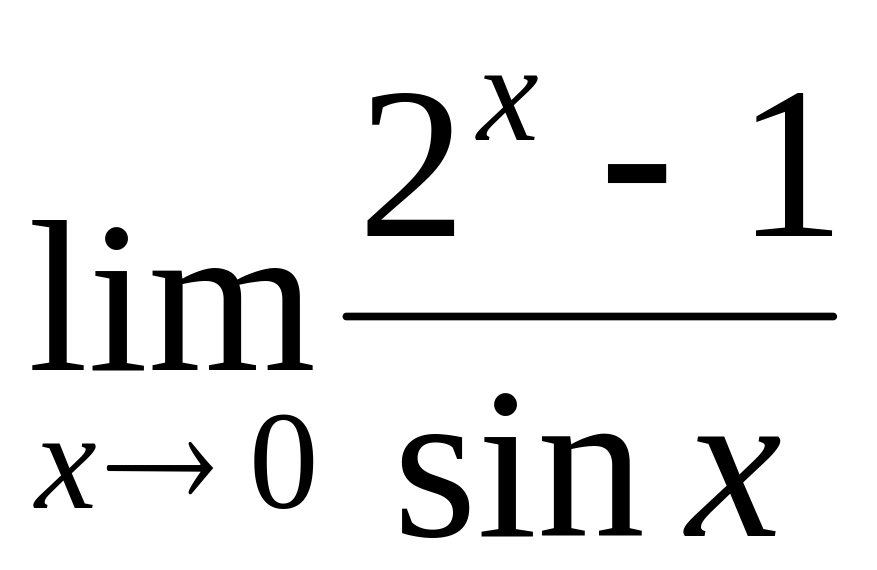 by means of Lhopital rule.
by means of Lhopital rule.Сalculate a limit
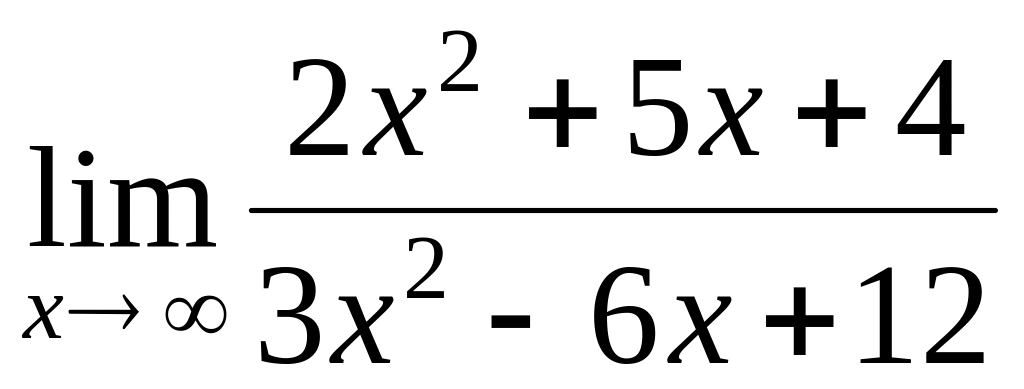 by means of Lhopital rule.
by means of Lhopital rule.Find a limit
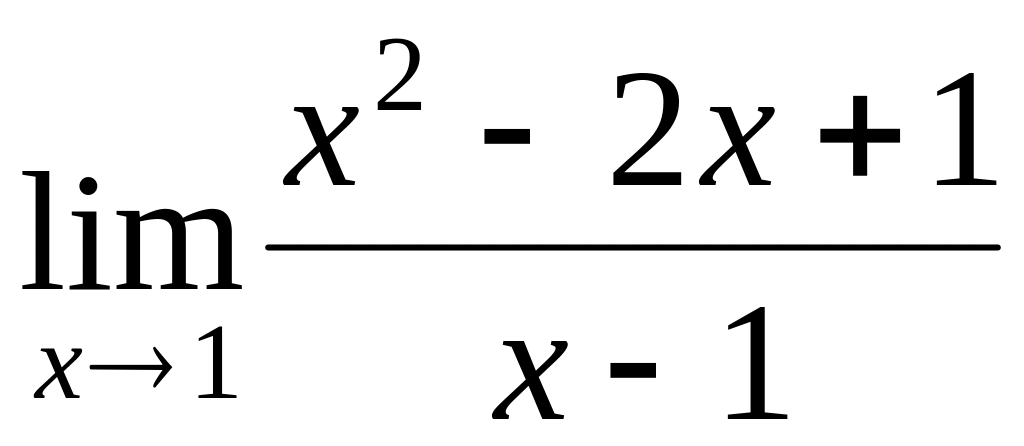 .
.Find a limit
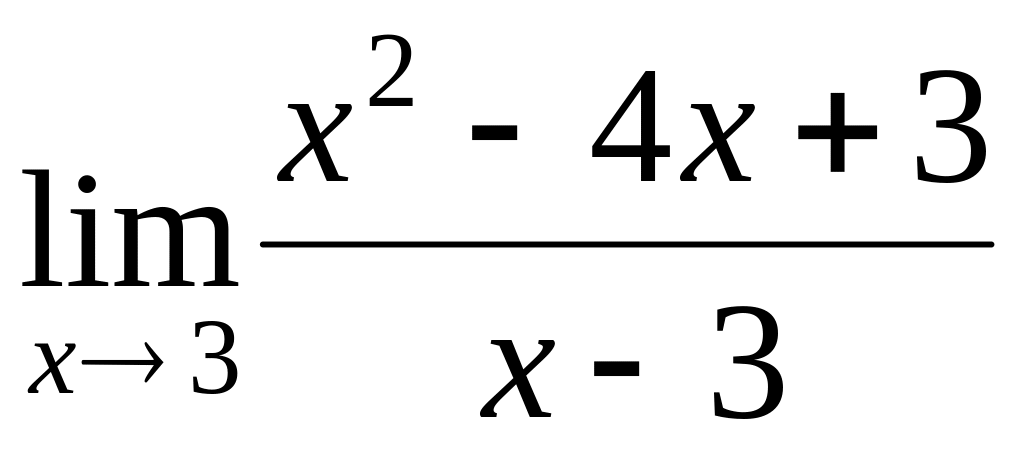 .
.Find a limit
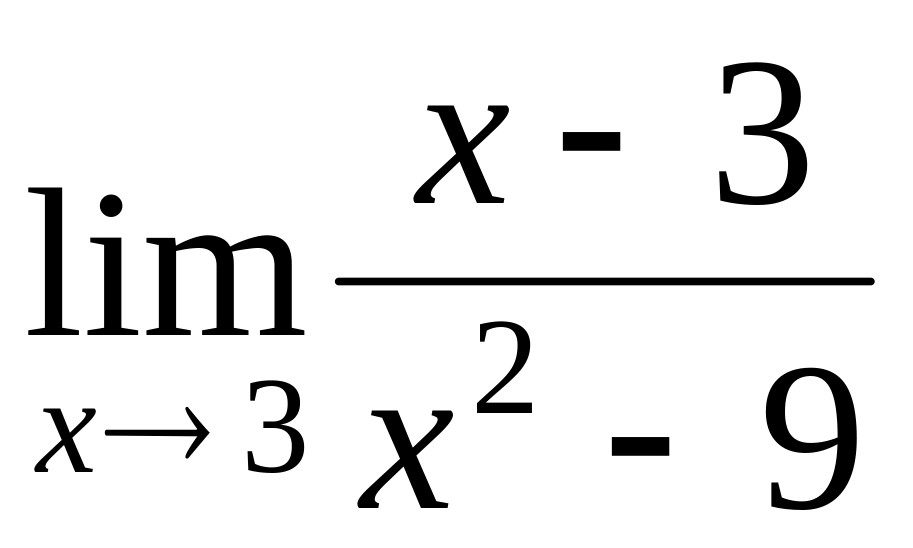 .
.Find a limit
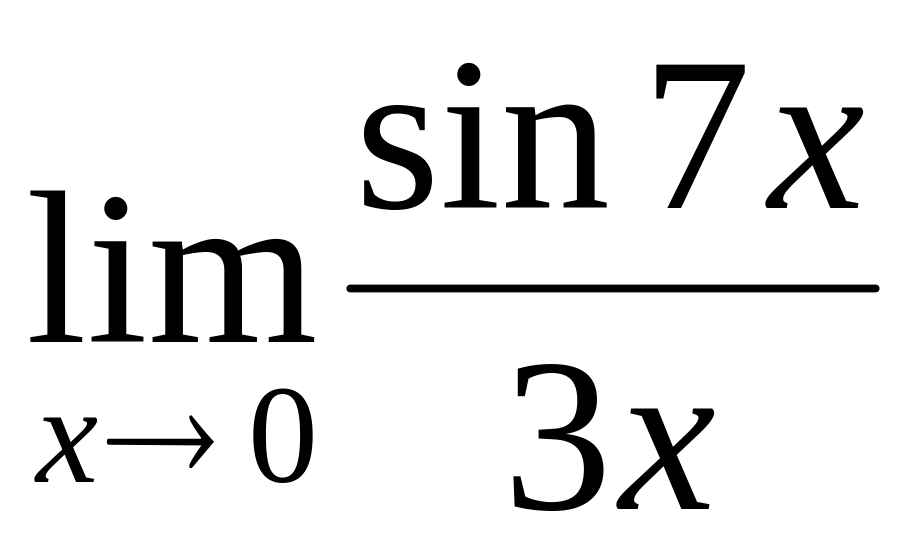 .
.Find the first remarkable limit.
Find the second remarkable limit.
Find a limit
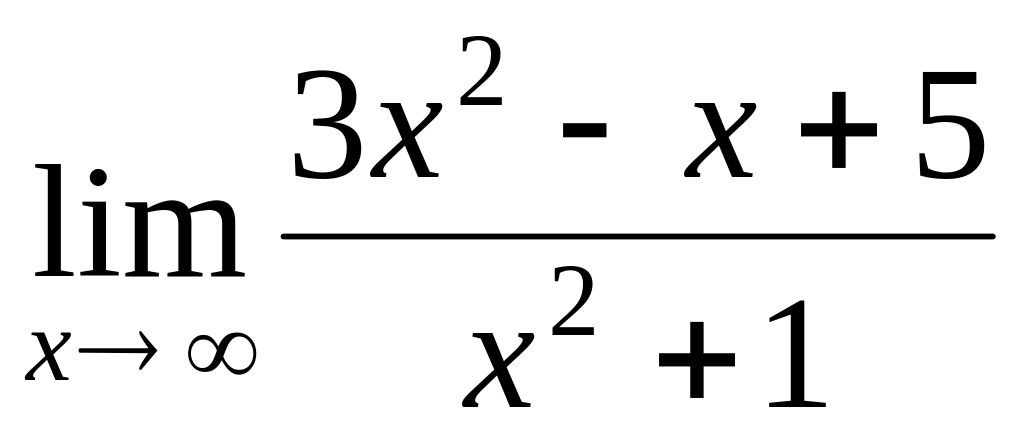 .
.Сalculate a limit
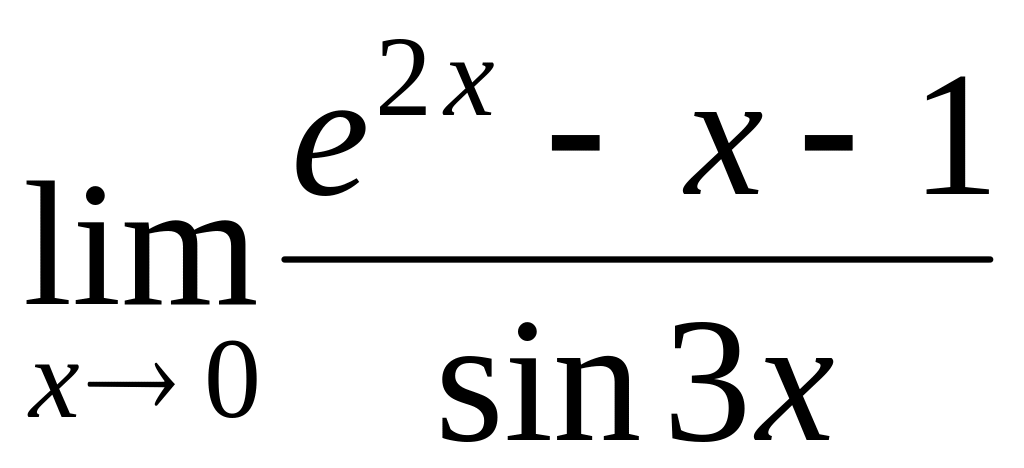 by means of Lhopital rule.
by means of Lhopital rule.Find a domain of function
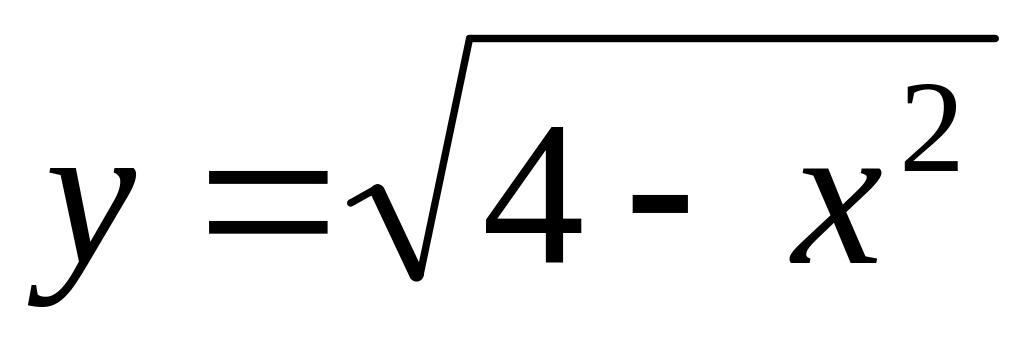 .
.Find a domain of function
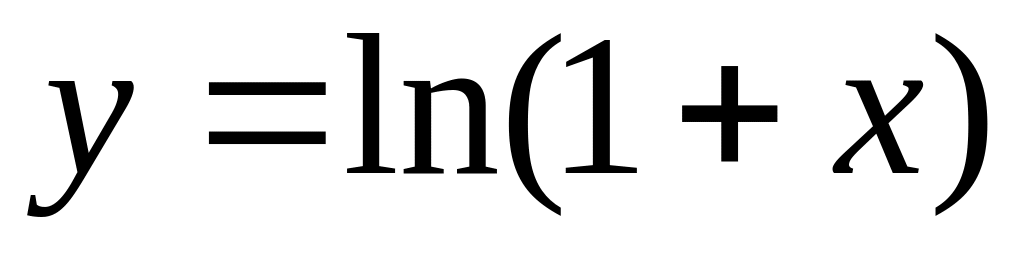 .
.Find a limit
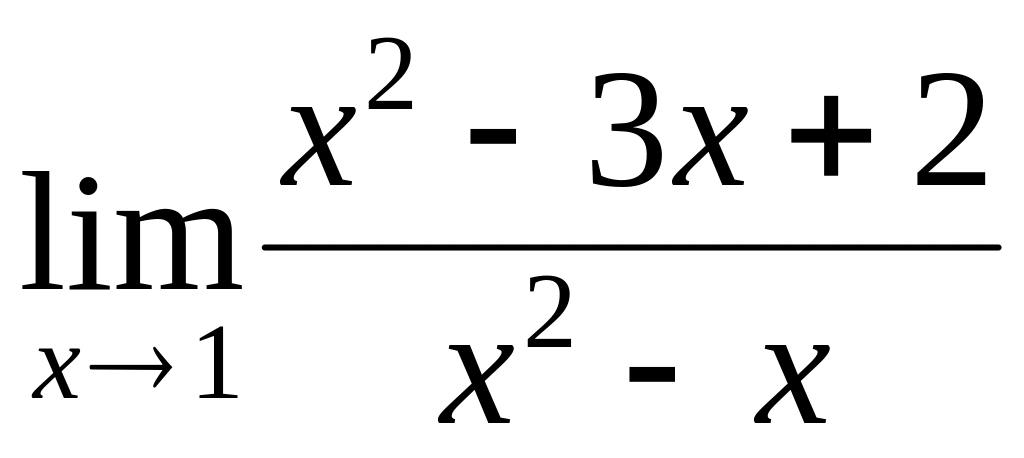 .
.
Find a limit
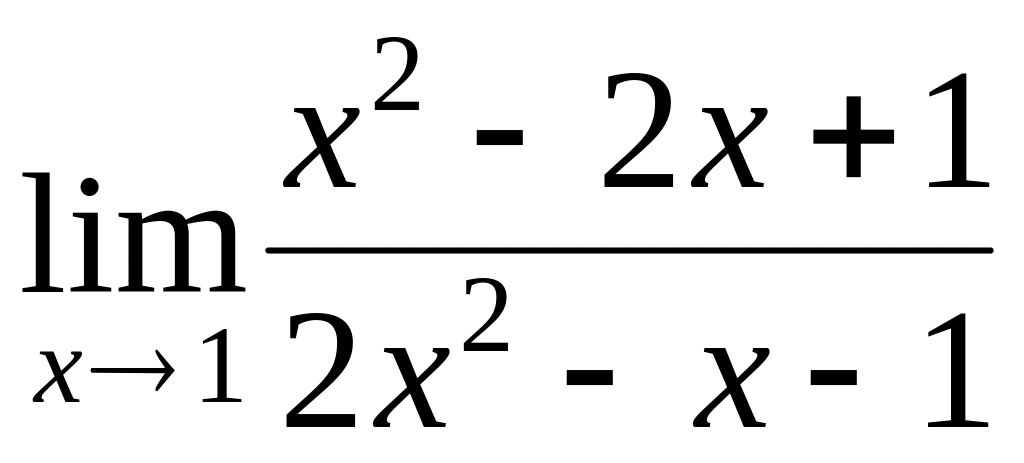 .
.Find a limit
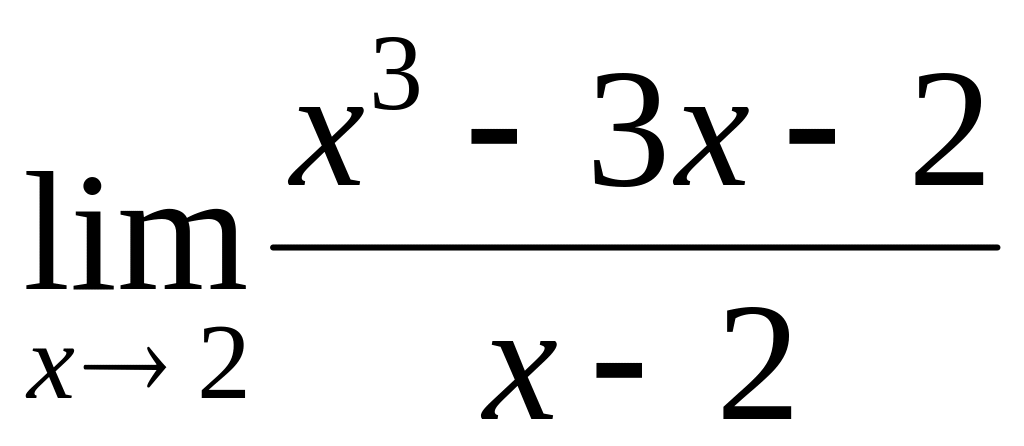 .
.Find a limit
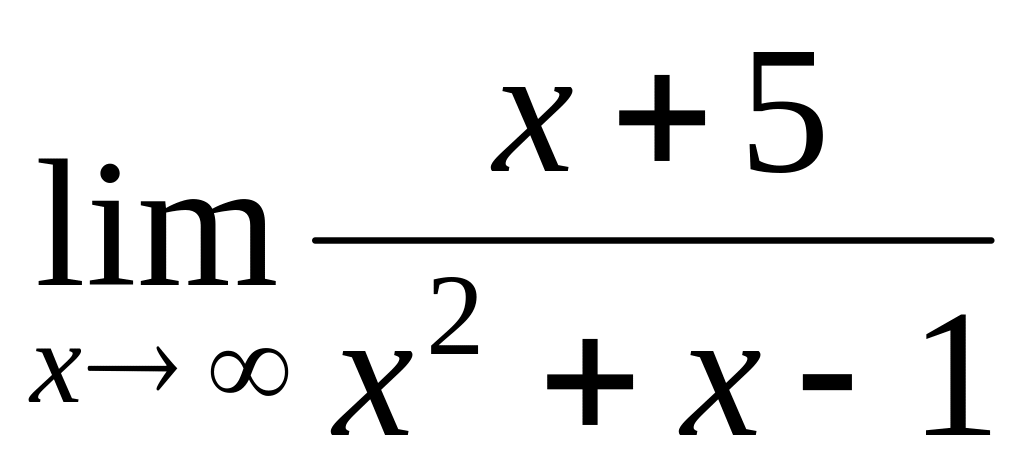 .
.
Find a limit
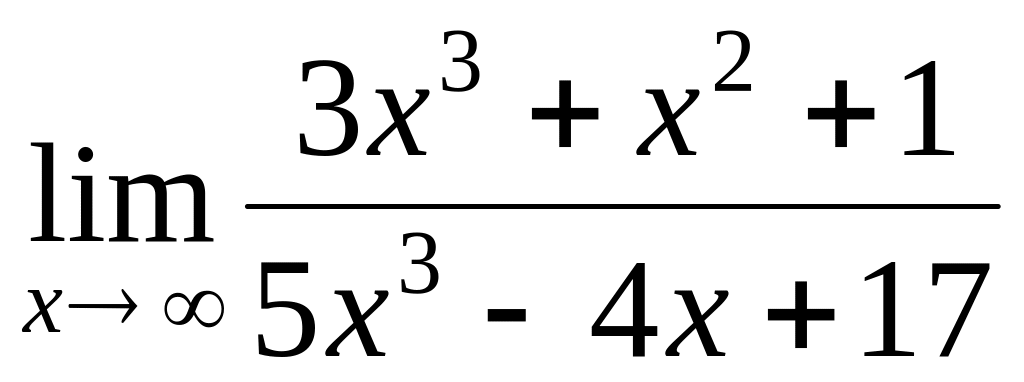 .
.Find a limit
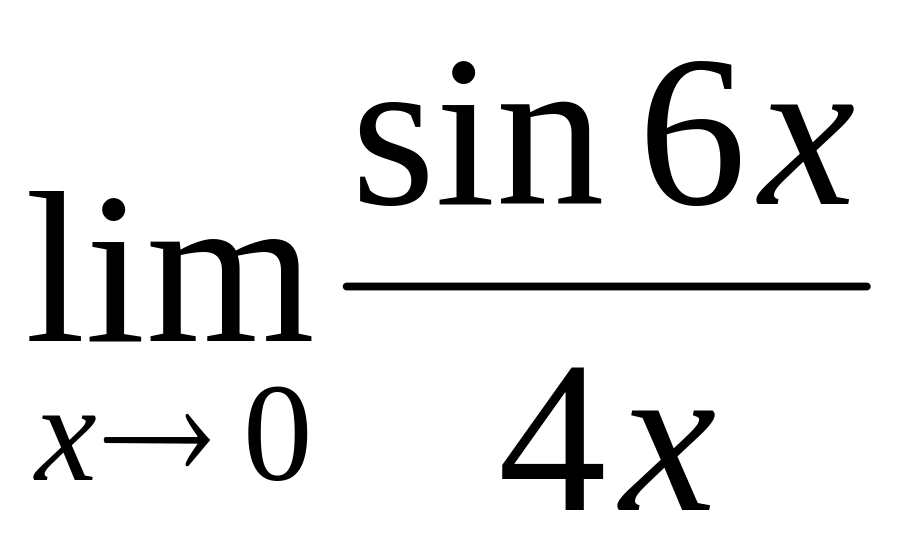 .
.Find a limit
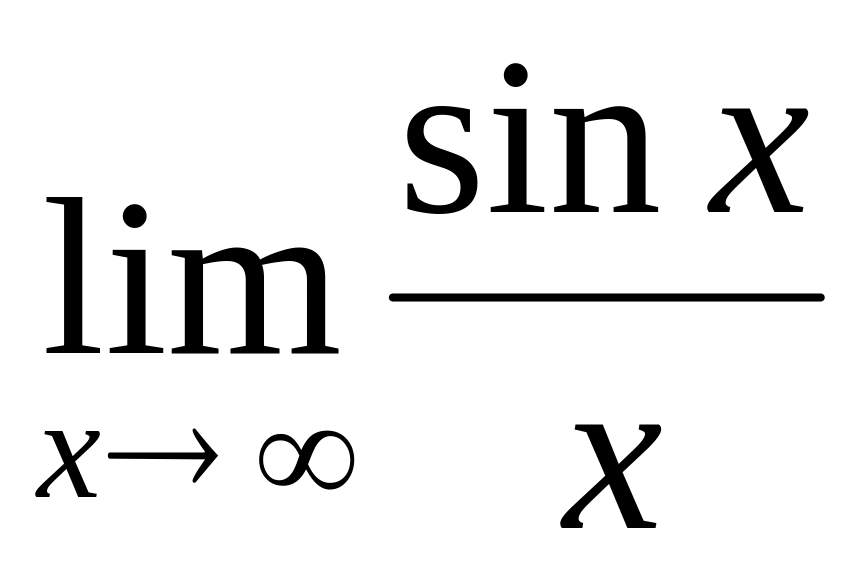 .
.Сalculate a limit
 by means of Lhopital rule.
by means of Lhopital rule.Сalculate a limit
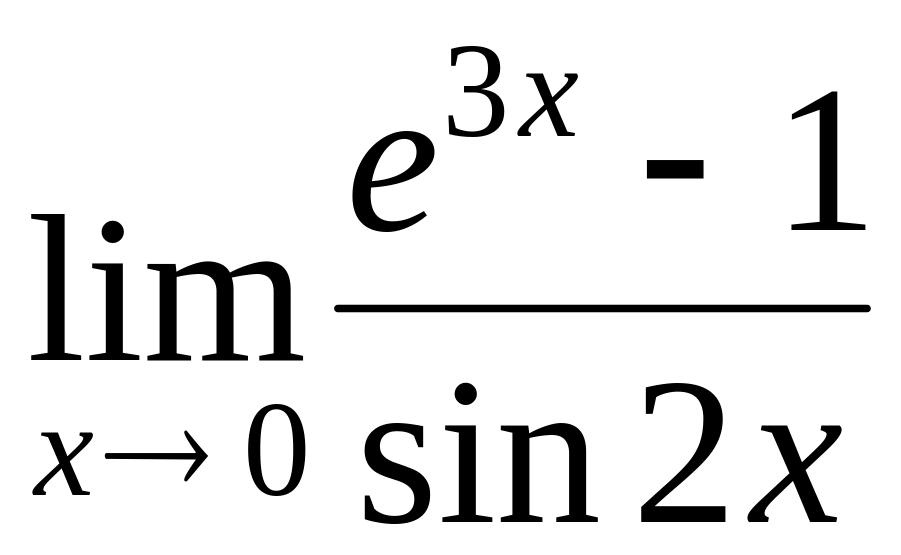 by means of Lhopital rule.
by means of Lhopital rule.Сalculate a limit
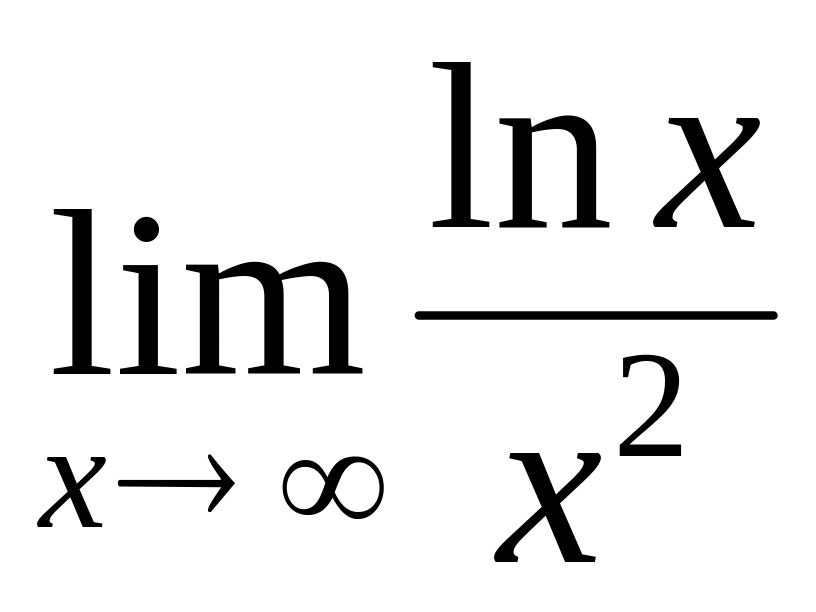 by means of Lhopital rule.
by means of Lhopital rule.Find a limit
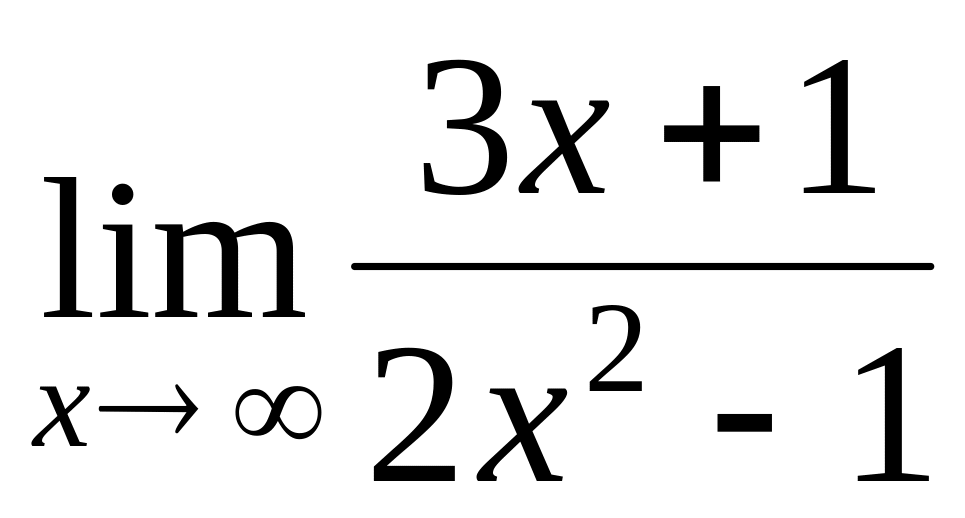 .
.Find a limit
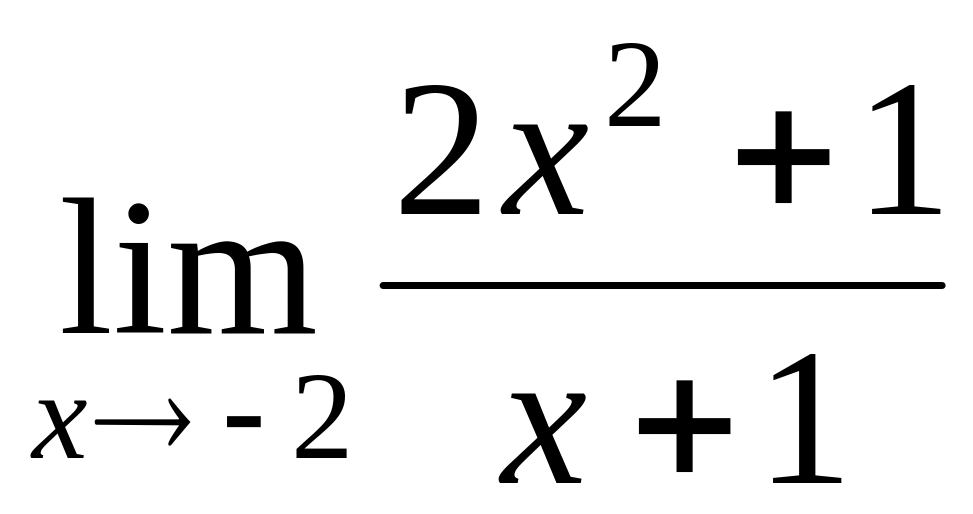 .
.Find a limit
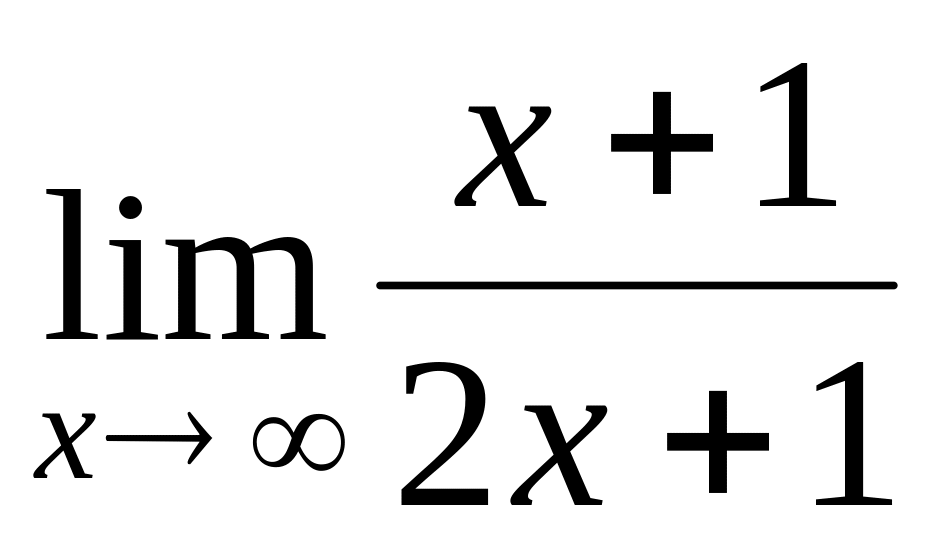 .
.Find a limit
 .
.Find a limit
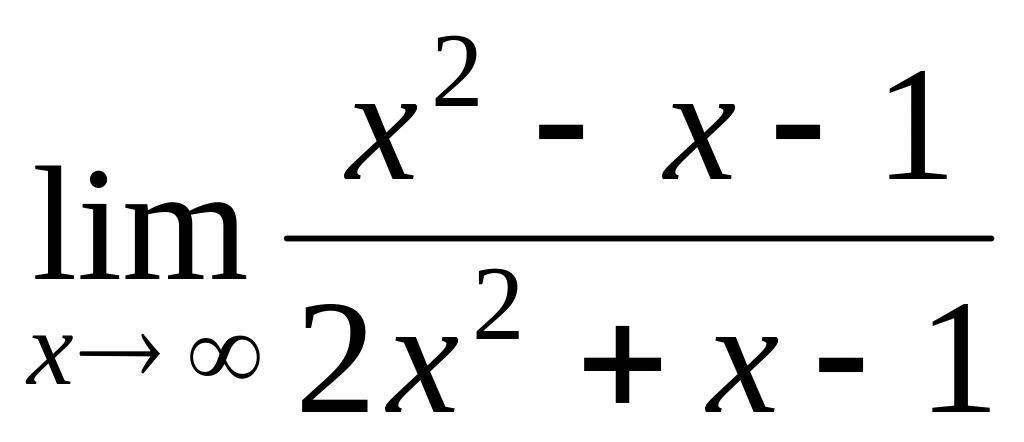 .
.Find a limit
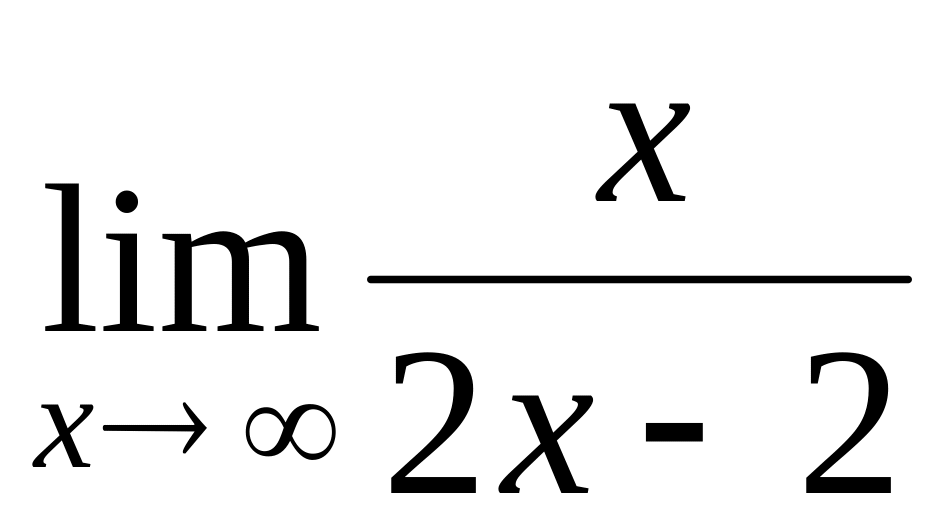 .
.Find a limit
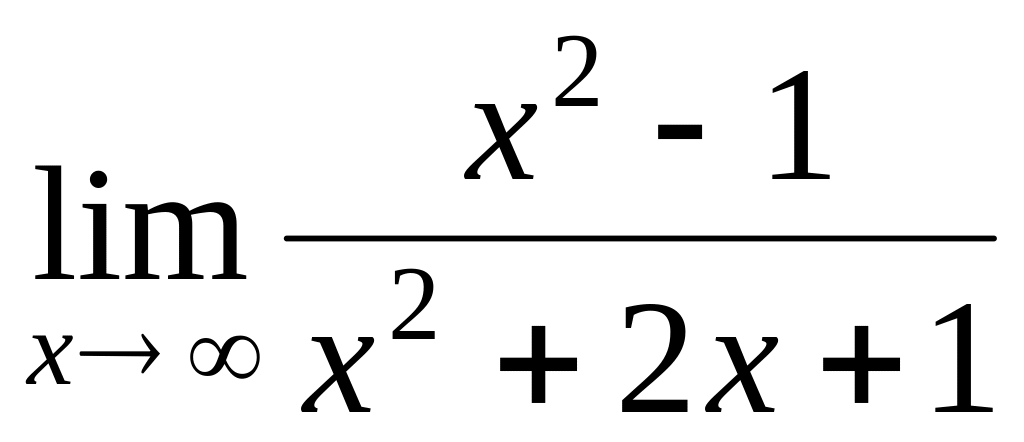 .
.Find a limit
 .
.Find a limit
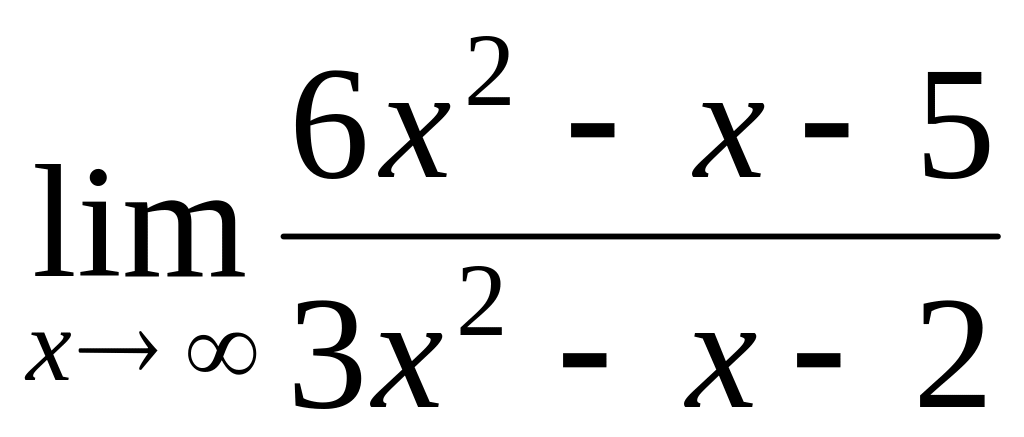 .
.Find a limit
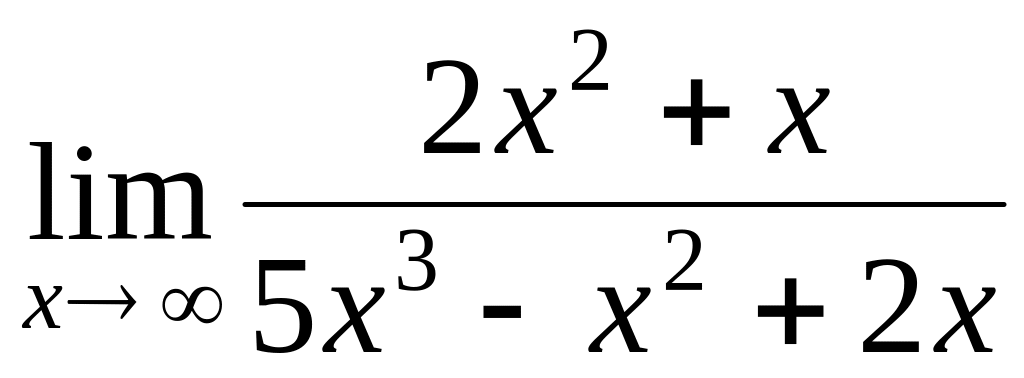 .
.Find a limit
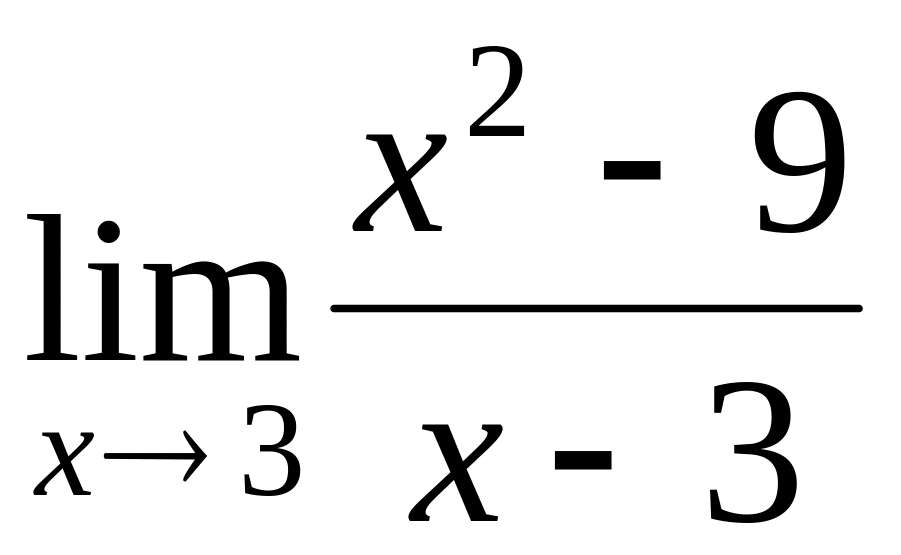 .
.Find a limit
 .
.Find a limit
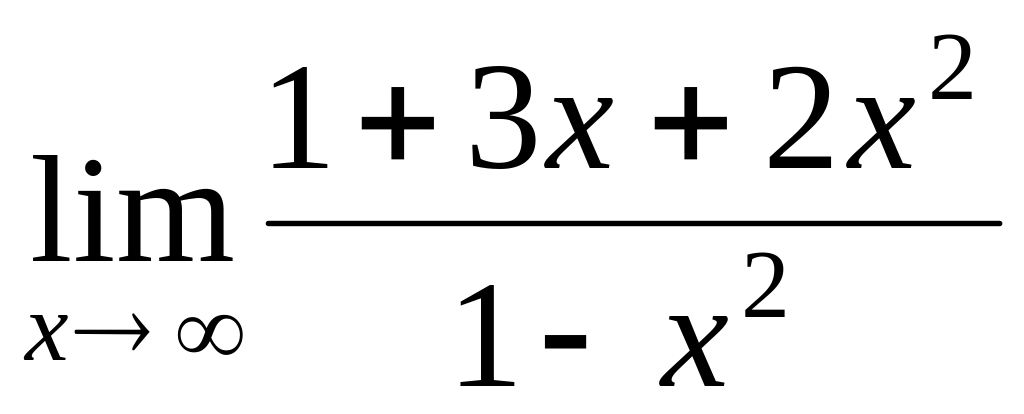 .
.Find a limit
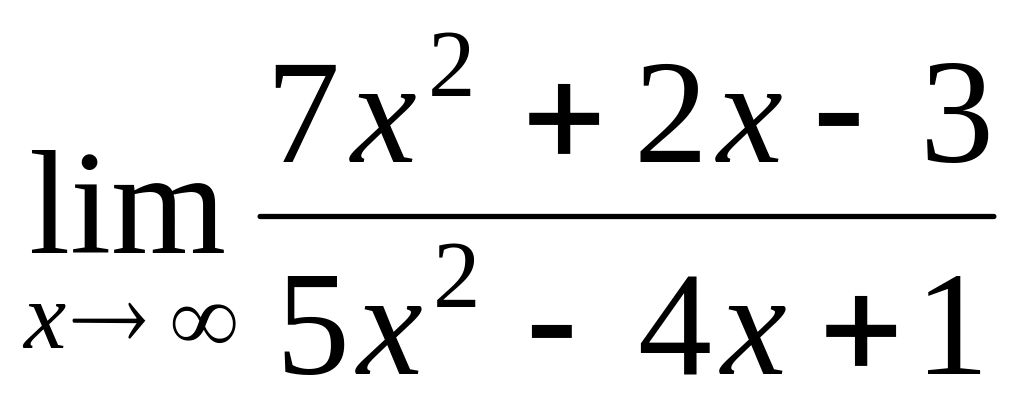 .
.
Theme 6. Derivative and differential of function
Derivative of function
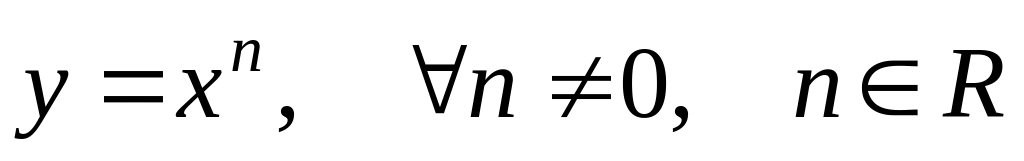 is equal:
is equal:Find the formula of a derivative of quotient
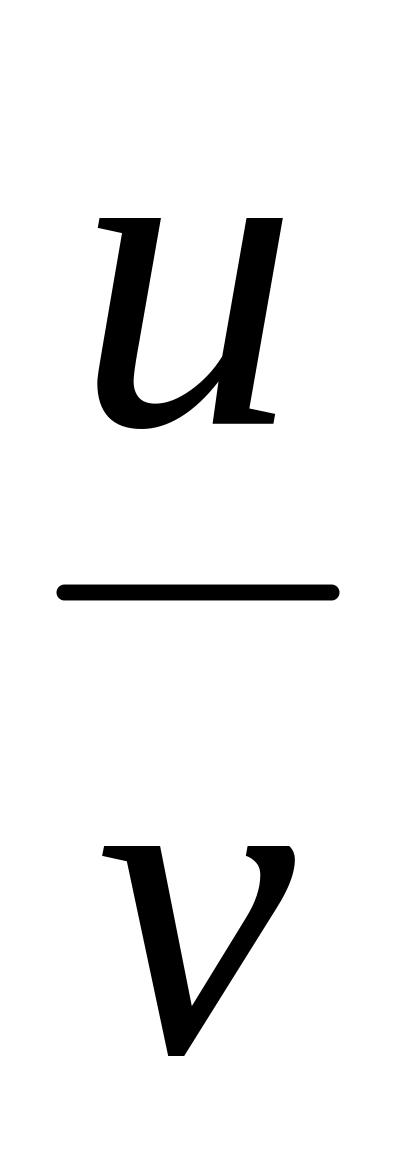 of two functions
of two functions
 and
and
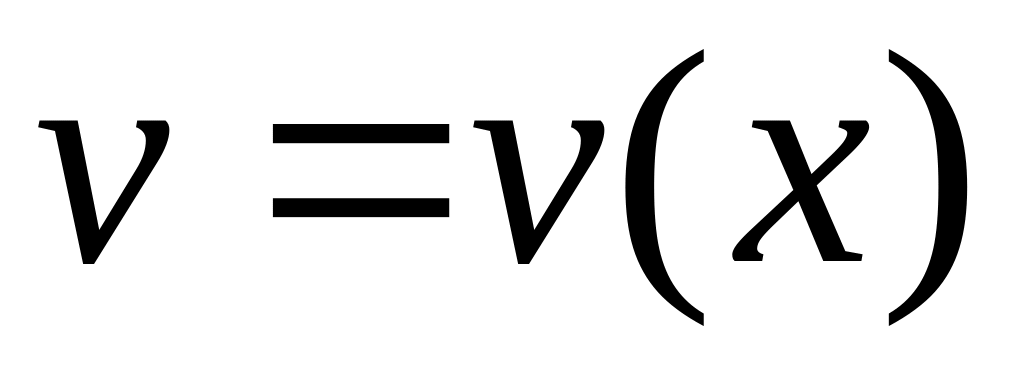 .
.Find the formula of derivative of exponential
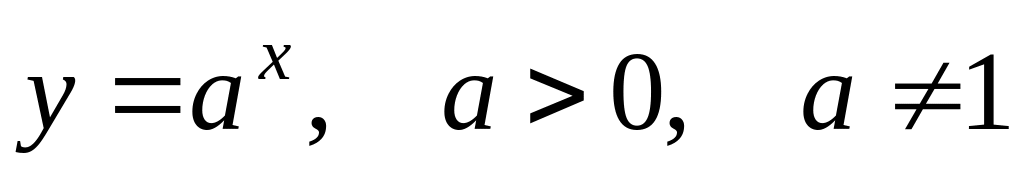 .
.Find the formula of derivative of logarithmic function
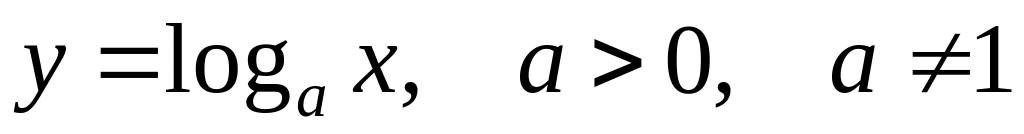 .
.Find the formula of derivative of function
 .
.Find a derivative of function
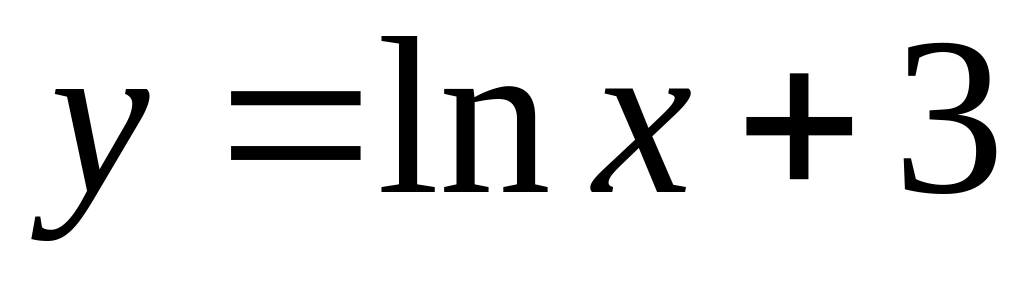 .
.Find a derivative of function
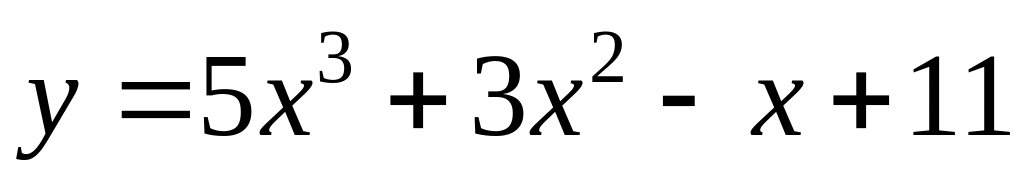 .
.Function
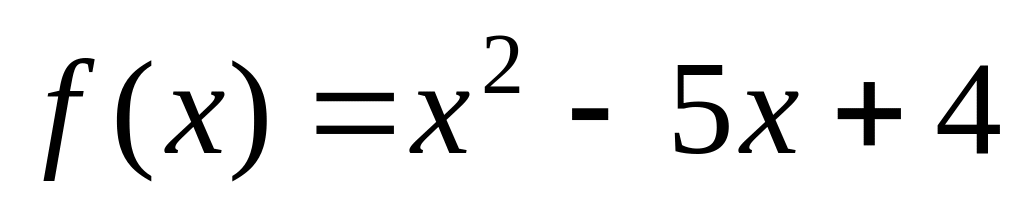 is
given. Сalculate value
is
given. Сalculate value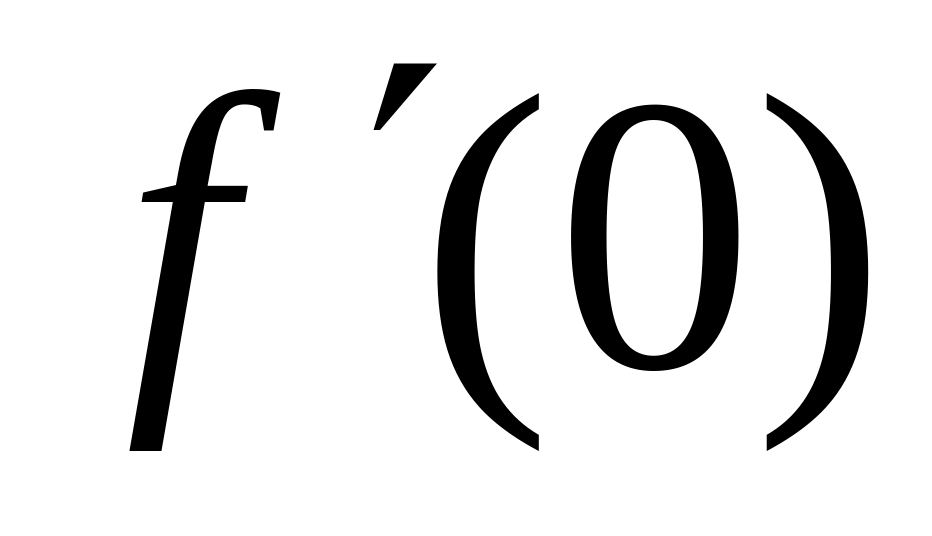 .
.Find a derivative of function
 .
.Function
 is given. Calculate value
is given. Calculate value
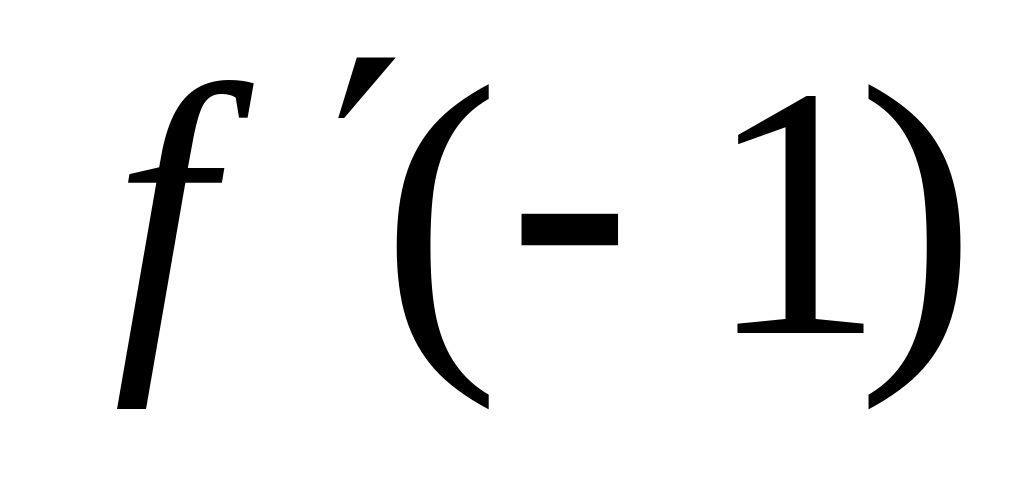 .
.Find a derivative of function
 .
.Find a derivative of function
 .
.Function
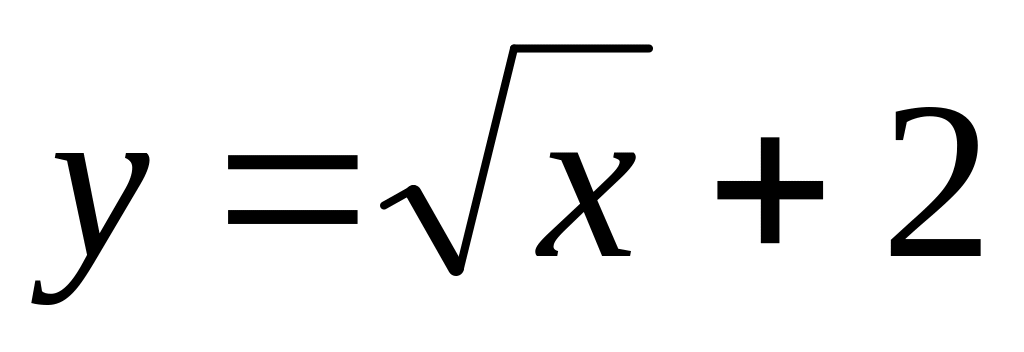 is
given. Сalculate value
is
given. Сalculate value
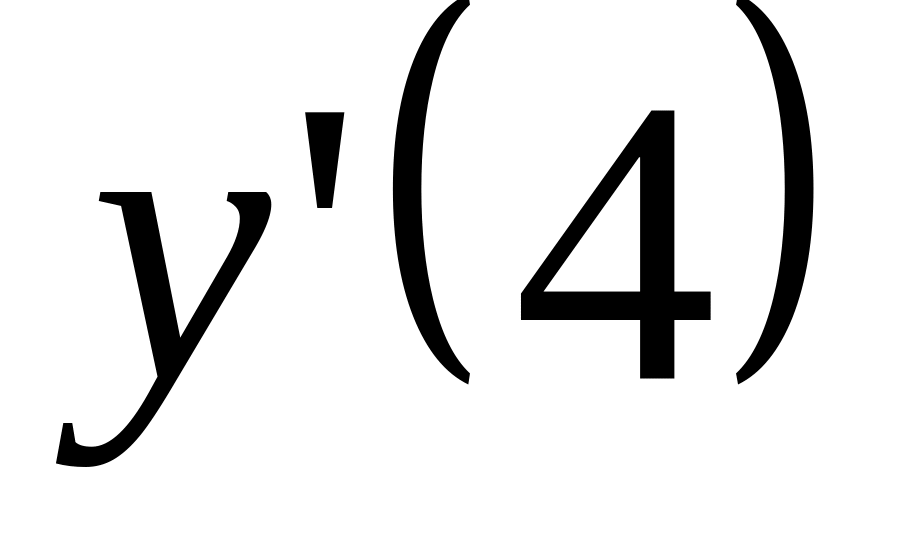 .
.Function
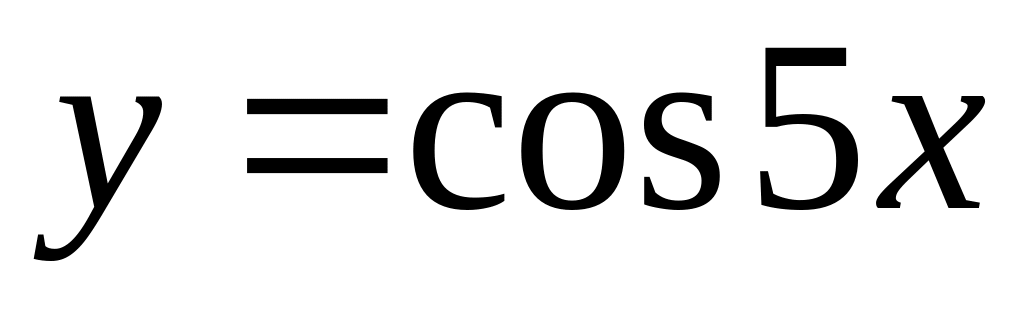 is given. Find
is given. Find
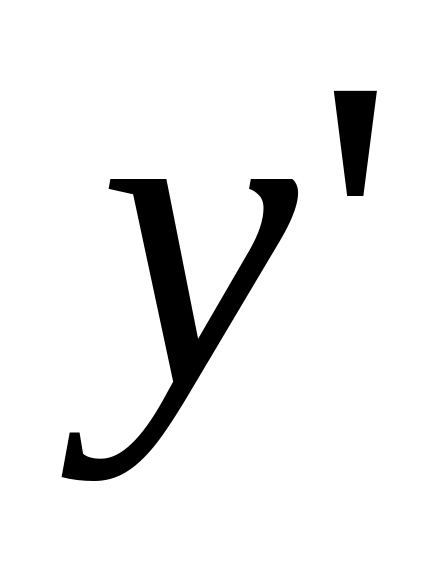 .
.Function
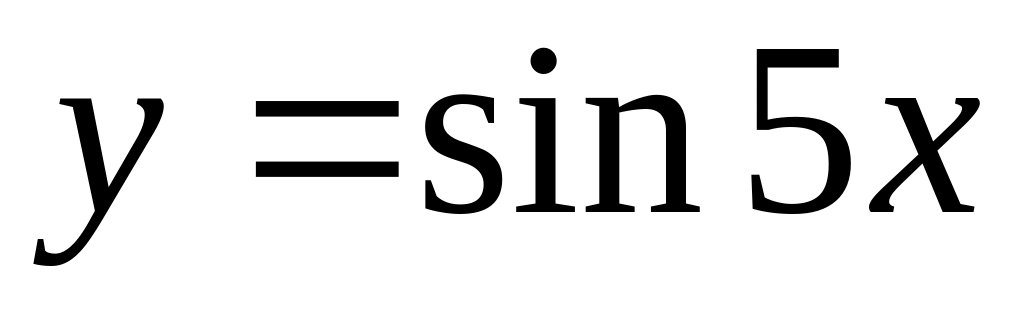 is given. Find
.
is given. Find
.Function
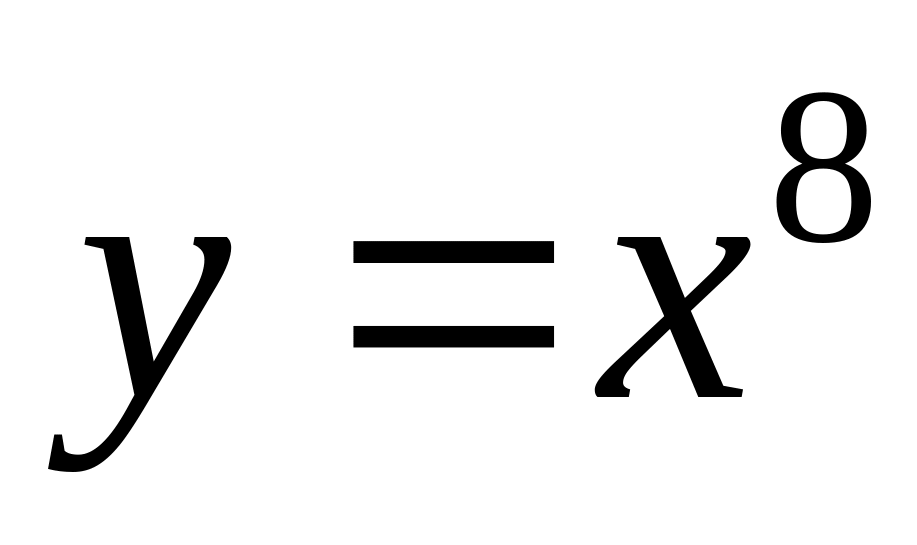 is given. Find
is given. Find
 .
.Function
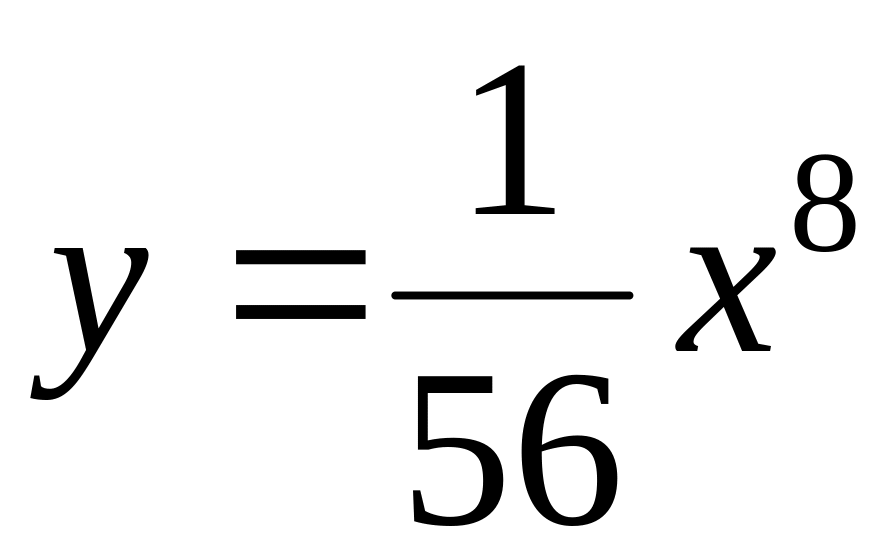 is given. Find
.
is given. Find
.Function
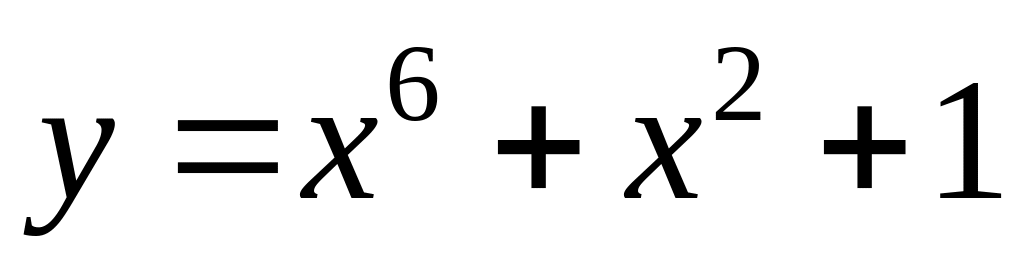 is given. Find
.
is given. Find
.Find the formula of a derivative of product
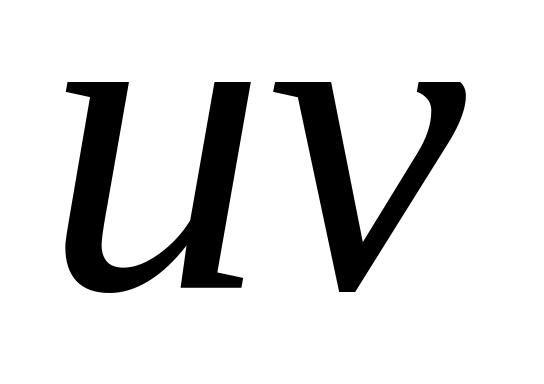 of two functions
and
.
of two functions
and
.Find the formula of derivative
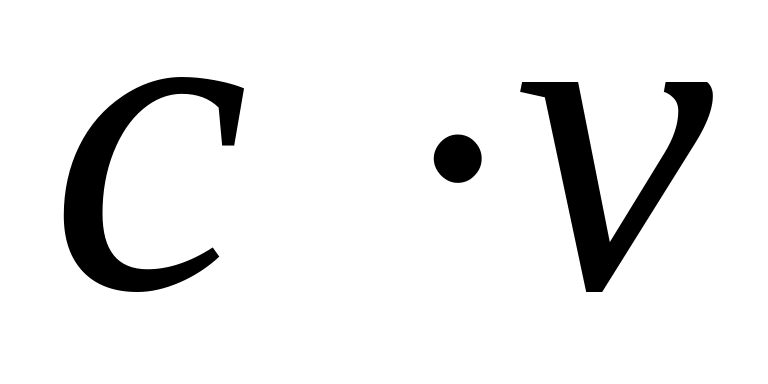 of function
of function
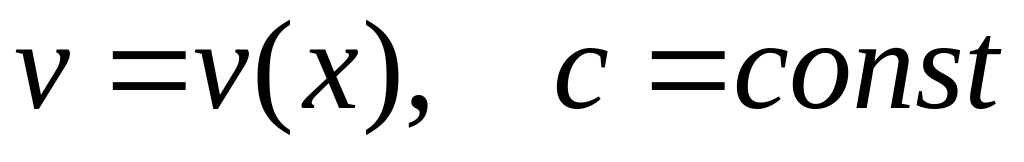 .
.Function is given. Calculate value .
Find a derivative of function
 .
.
Find a derivative of function
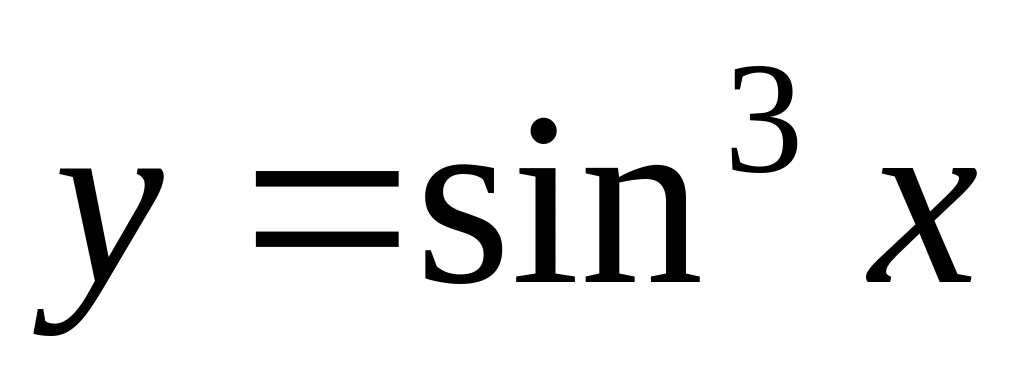 .
.Find differential of function
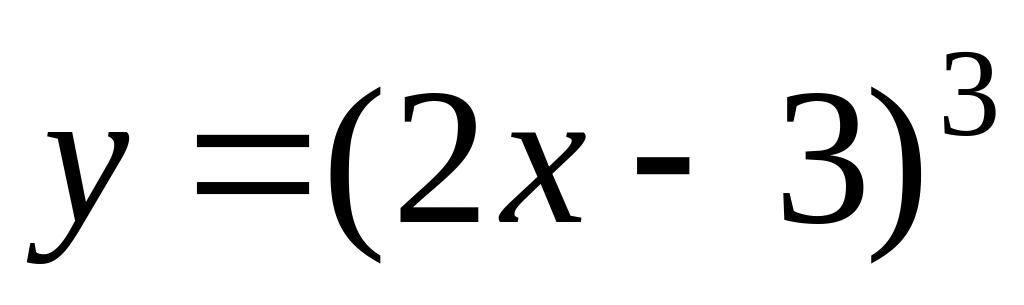 .
.Find a derivative of function
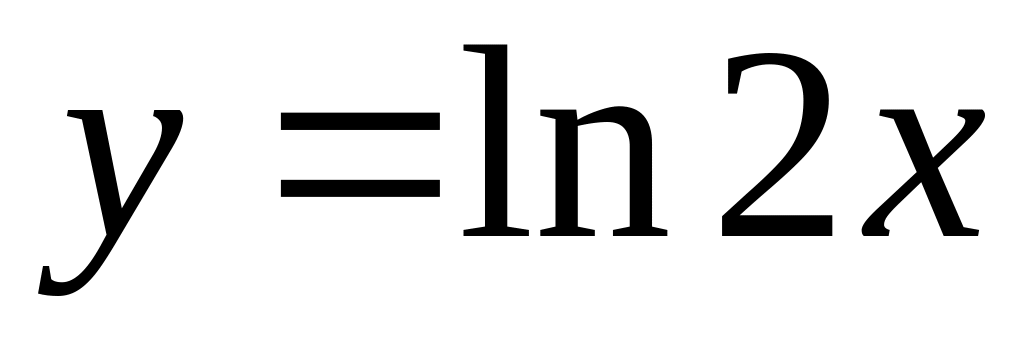 .
.Function
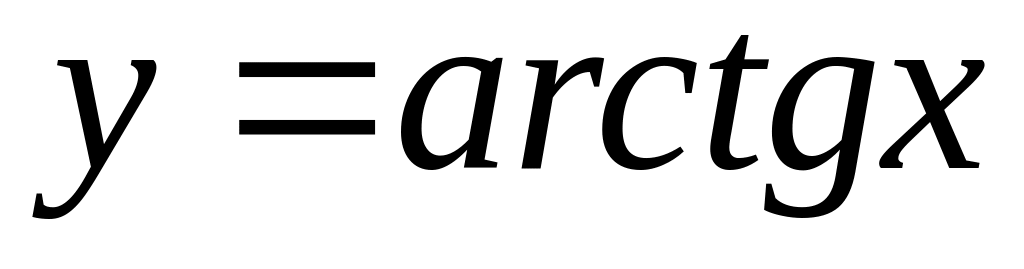 is
given. Find a derivative
.
is
given. Find a derivative
.Derivative of function
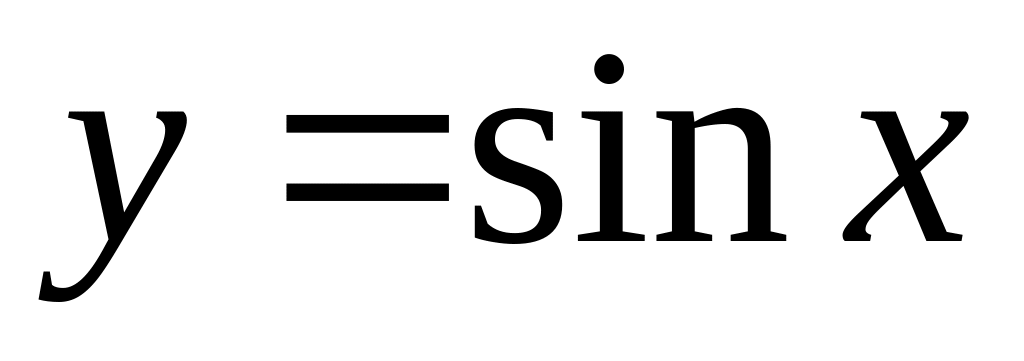 is equal:
is equal:Derivative of function
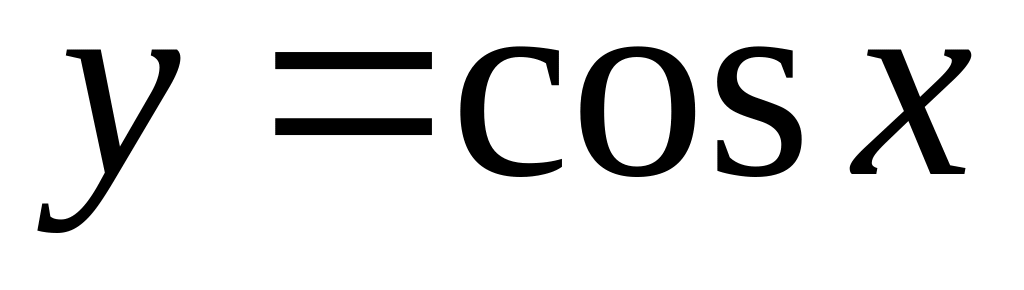 is equal:
is equal:Derivative of function
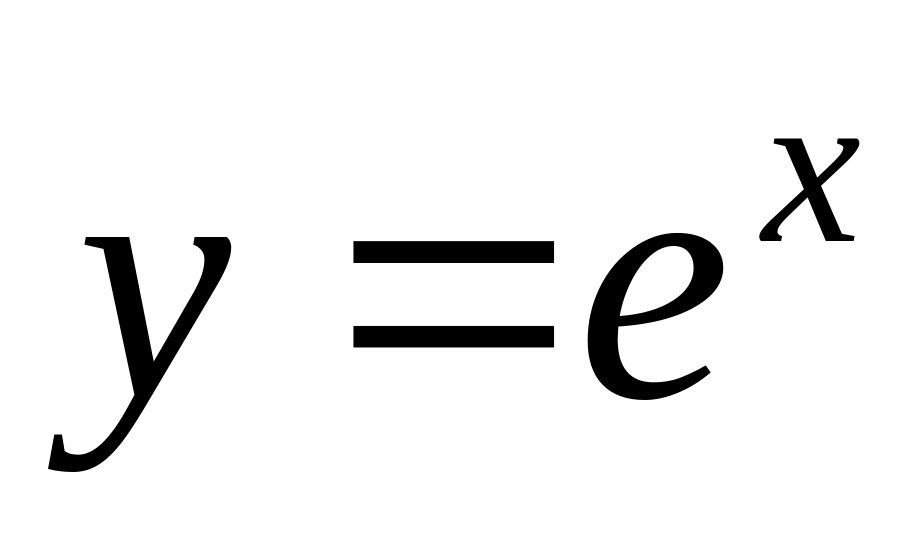 is equal:
is equal:Derivative of function
 is equal:
is equal:Derivative of function
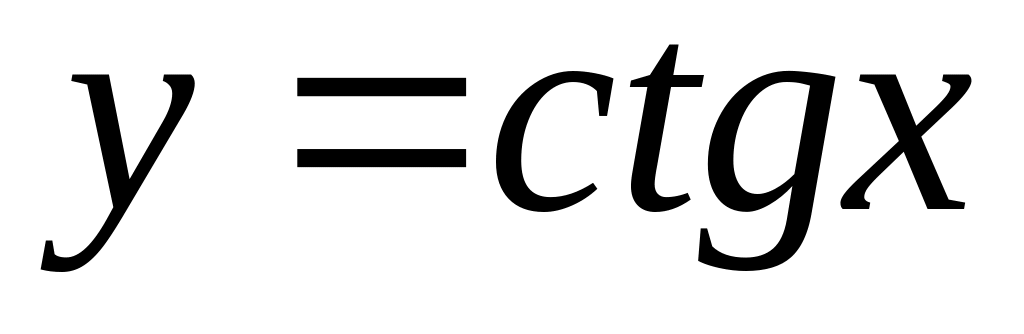 is equal:
is equal:Derivative of function
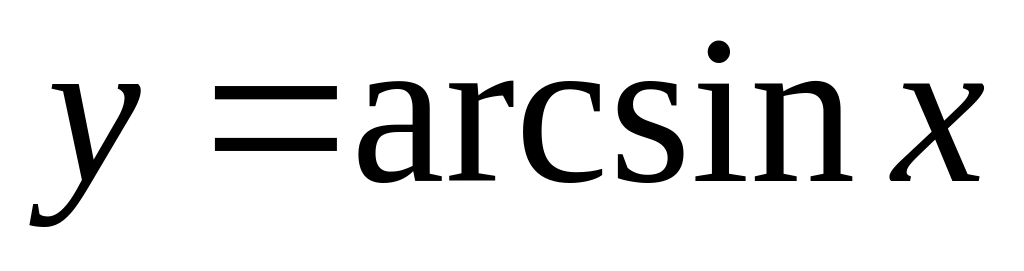 is equal:
is equal:Derivative of function
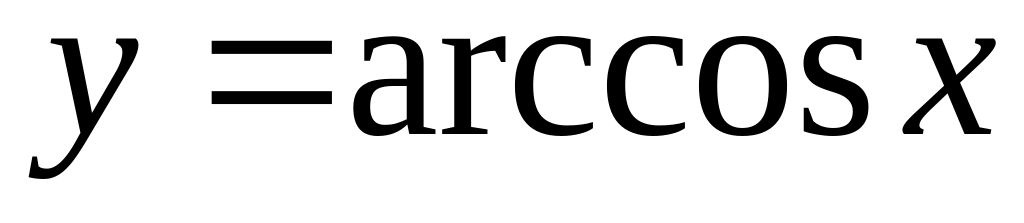 is equal:
is equal:Derivative of function is equal:
Derivative of function
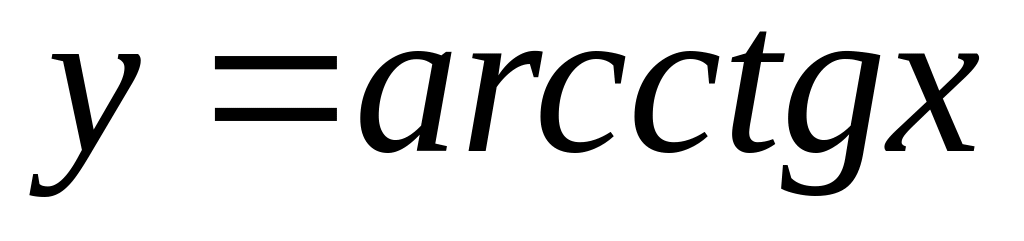 is equal:
is equal:Find a derivative of function
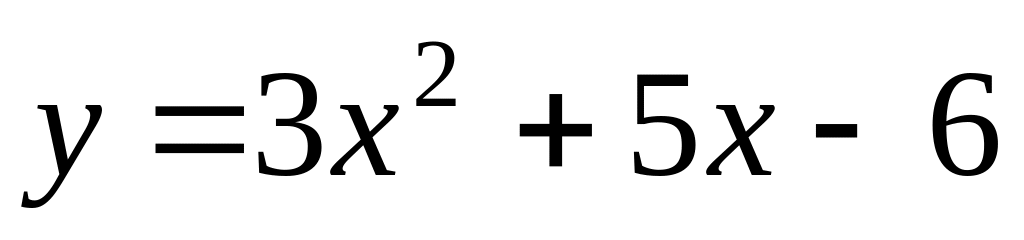 .
.Find a derivative of function
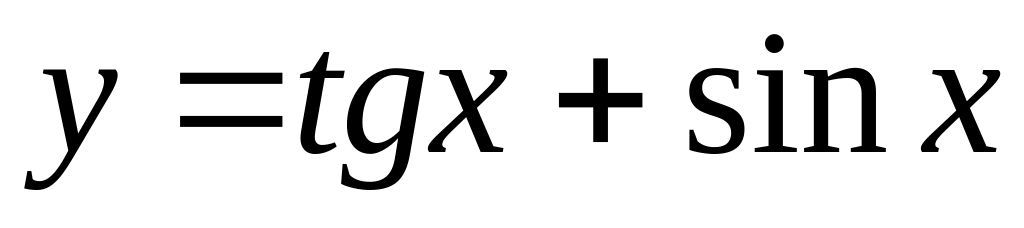 .
.Find a derivative of function
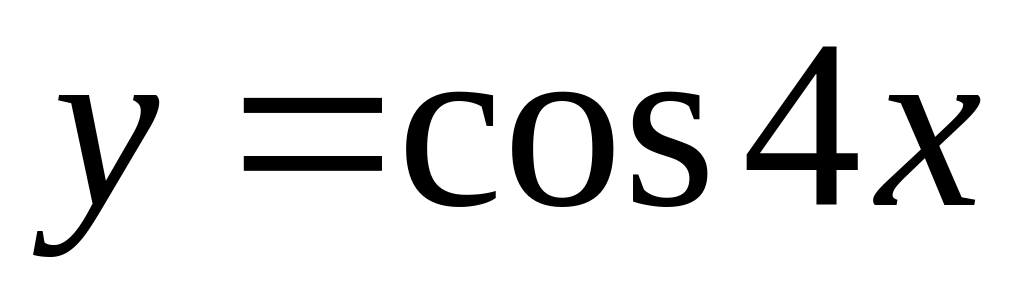 .
.Find a derivative of function
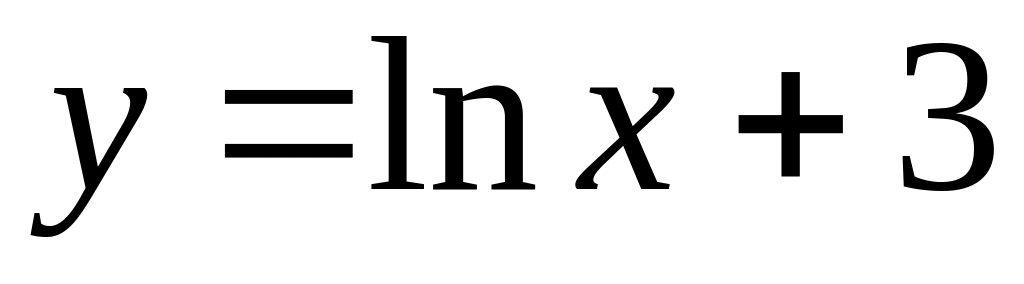 .
.Find a derivative of function
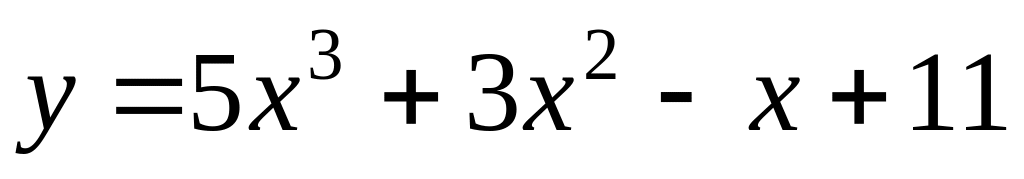 .
.Find a derivative of function
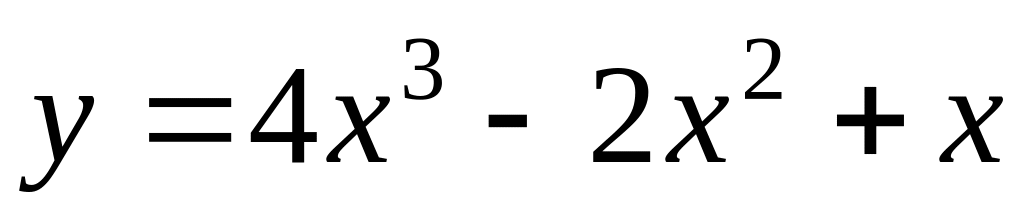 .
.
Find a derivative of function
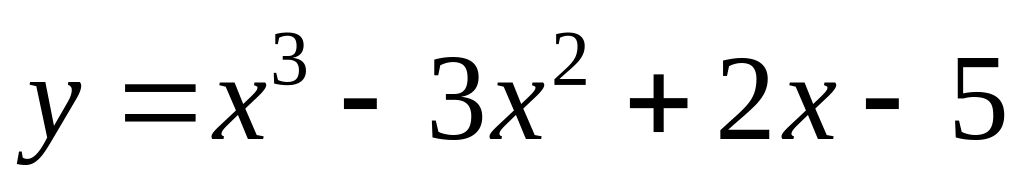 .
.Find a derivative of function
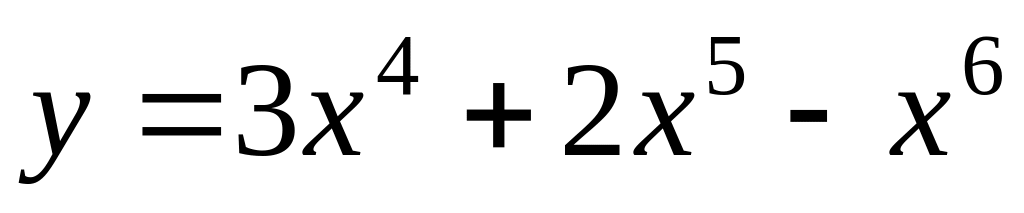 .
.Find a derivative of function
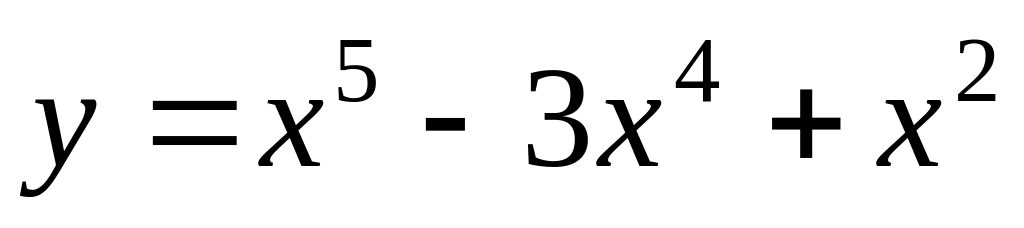 .
.
Find a derivative of function
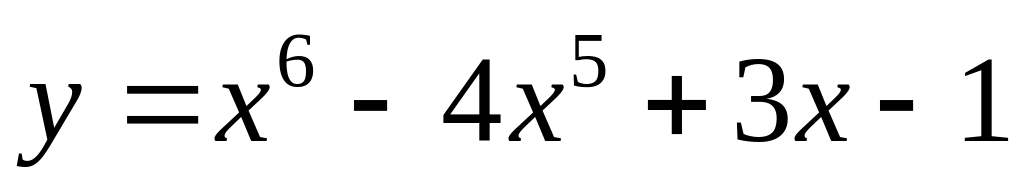 .
.
Theme 7. Investigation of function by means of a derivative
Find an interval of decrease of function
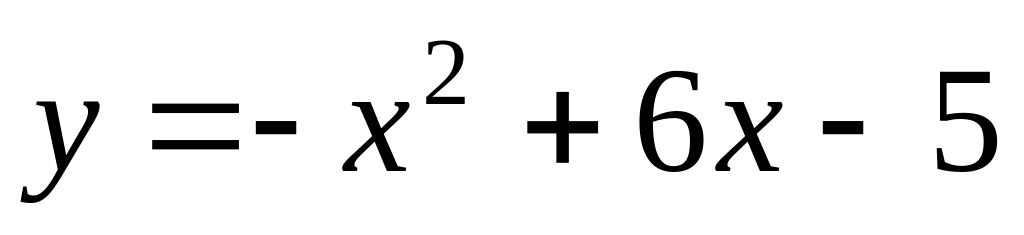 .
.Find an interval of increase of function
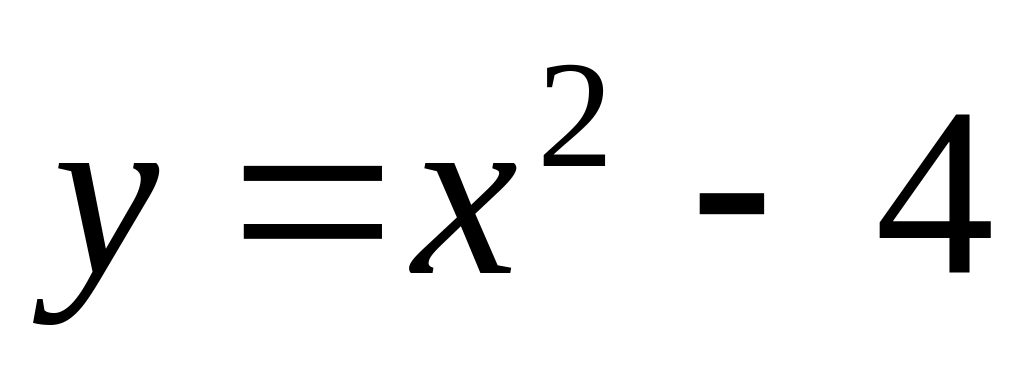 .
.Find an interval of increase of function
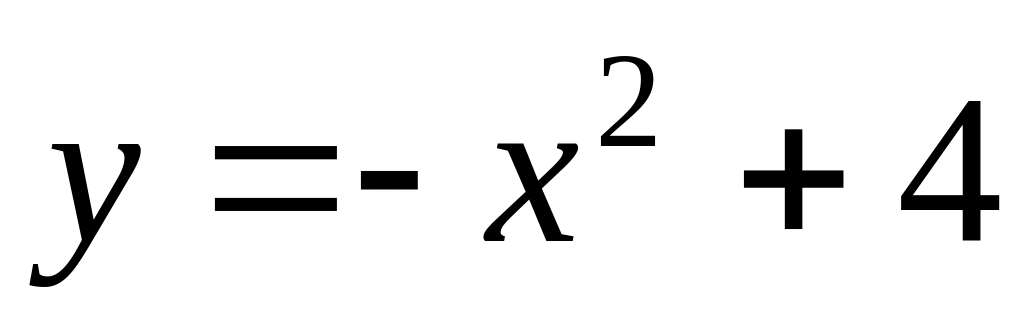 .
.Find an interval of convexity of function
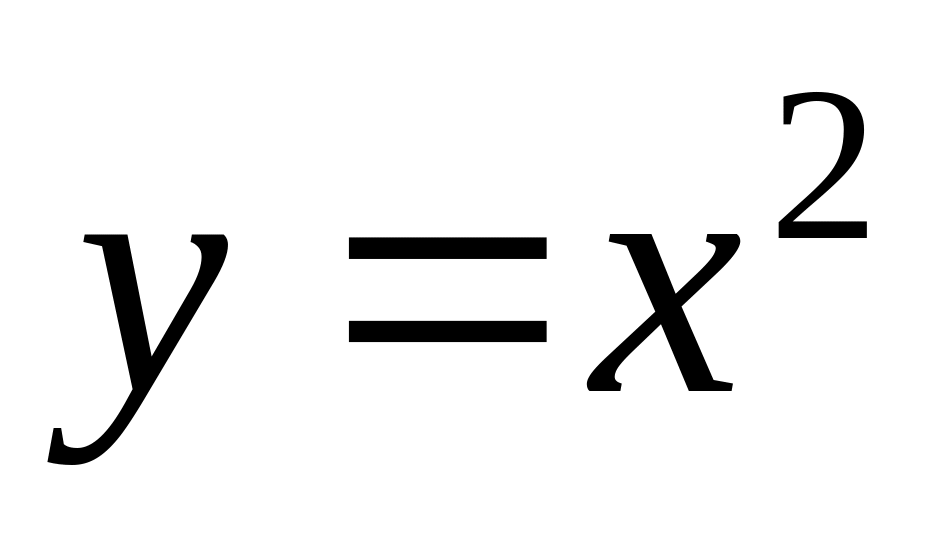 .
.Find an interval of concavity of function .
Find an interval of convexity of function
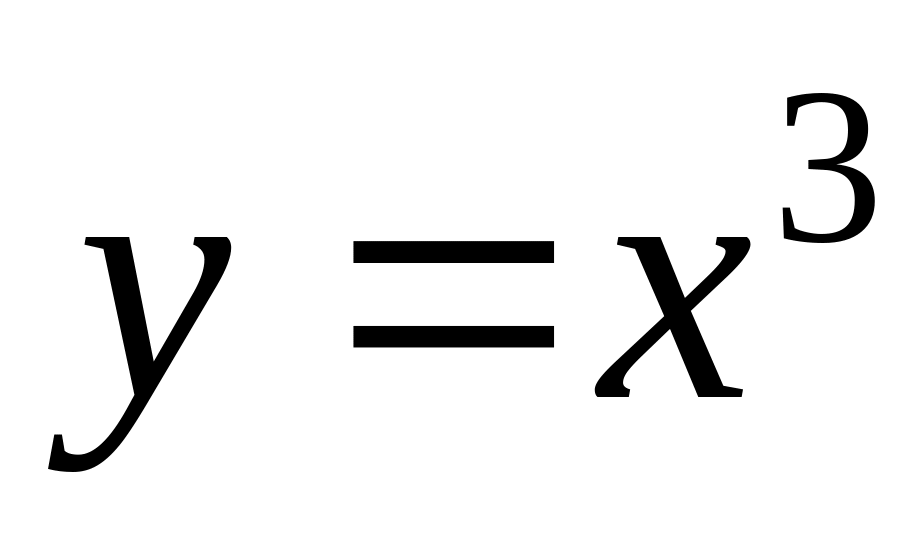 .
.Find an interval of concavity of function .
Find a point of a maximum of function
 .
.Find a point of a minimum of function
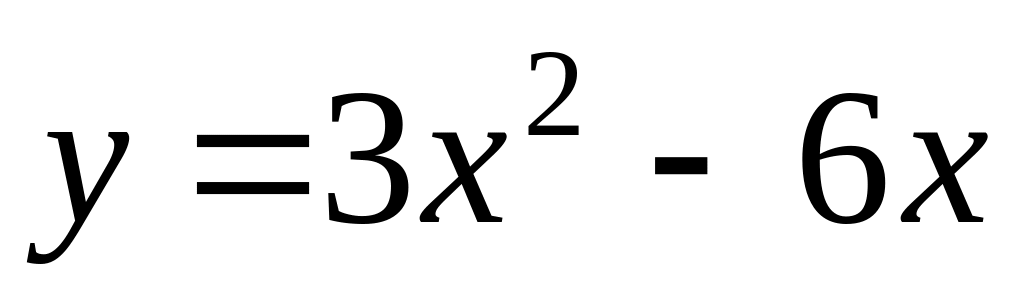 .
.Investigate function
 on an extremum.
on an extremum.If the derivative of differentiate function is positive inside of an interval
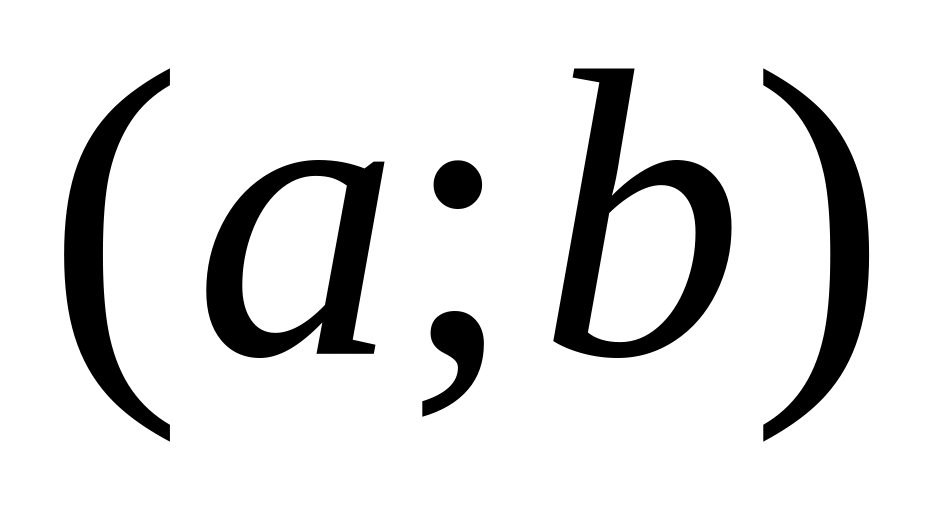 ,
then function on an interval
:
,
then function on an interval
:Necessary condition of an extremum of function in a point
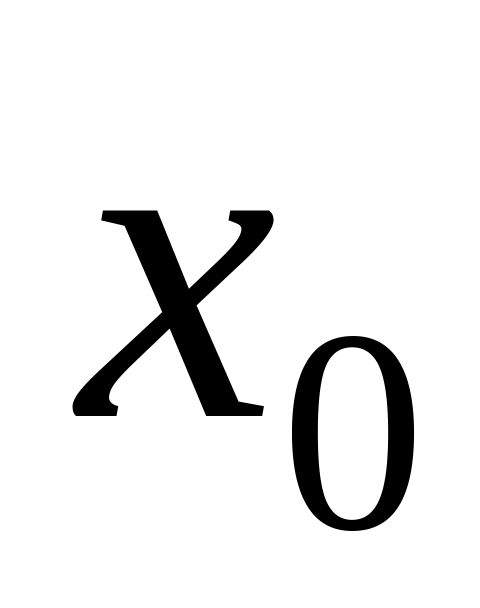 :
:If at transition through a critical point the derivative of function changes the sign from plus on a minus, then the point is a point:
Find interval of increase of function
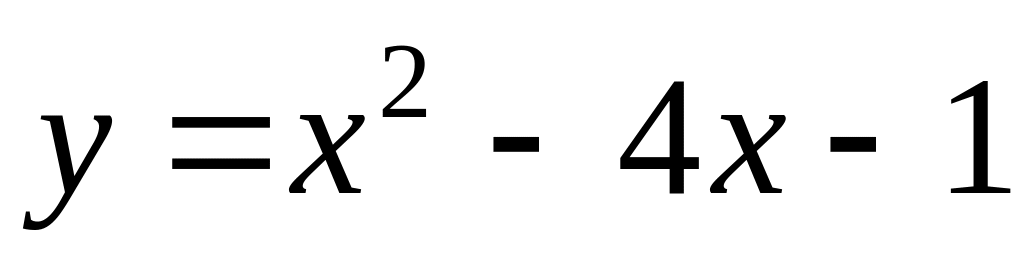 .
.Find a point of a minimum of function
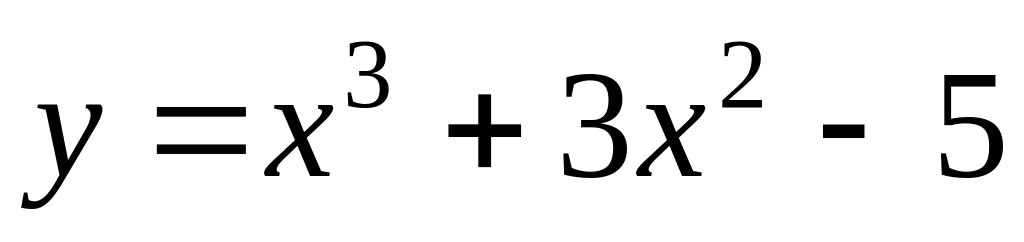 .
.Find a point of a maximum of function .
Find interval of decrease of function .
Find points of inflection of function
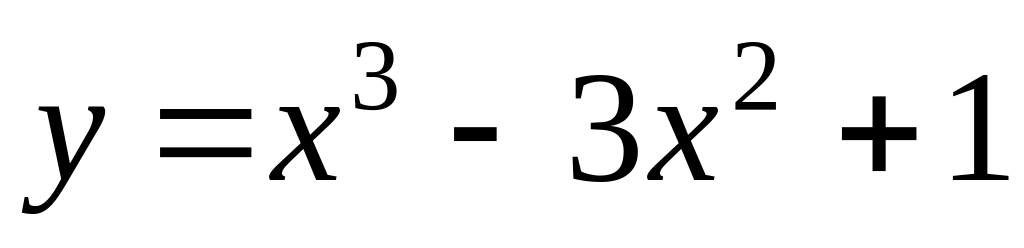 .
.Find points of inflection of a curve
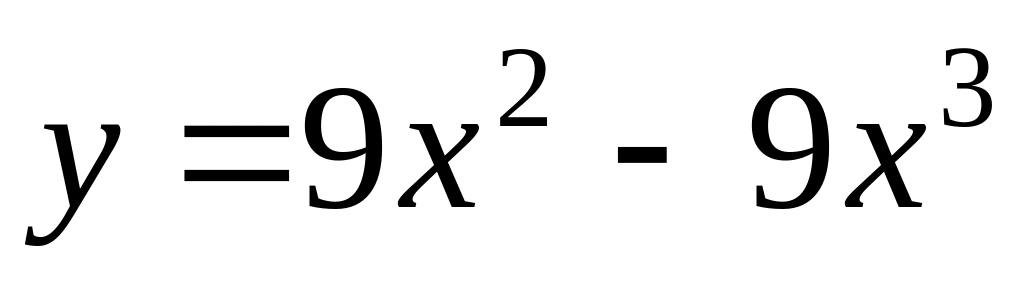 .
.Find an interval of convexity of the graph of function .
To what of following equality even function satisfies:
To what of following equality odd function satisfies:
Theme 8. Functions of several variables
Function
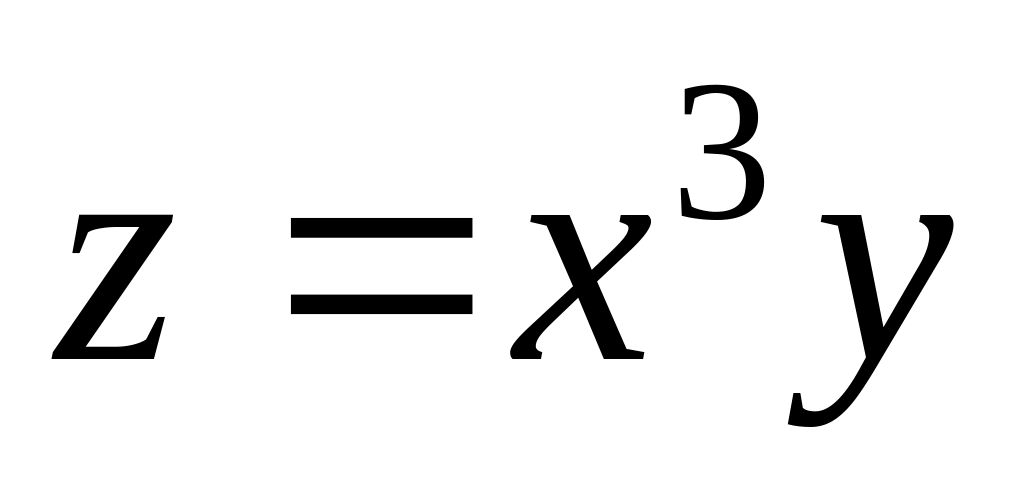 is
given. Find a partial derivative
is
given. Find a partial derivative
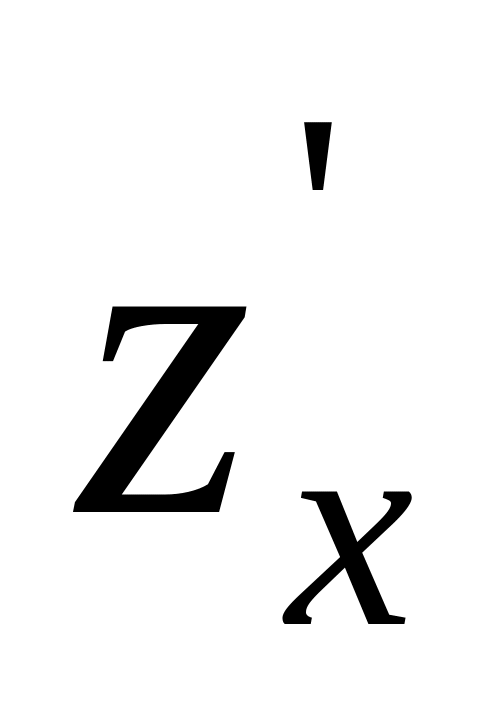 .
.Function is given. Find a partial derivative
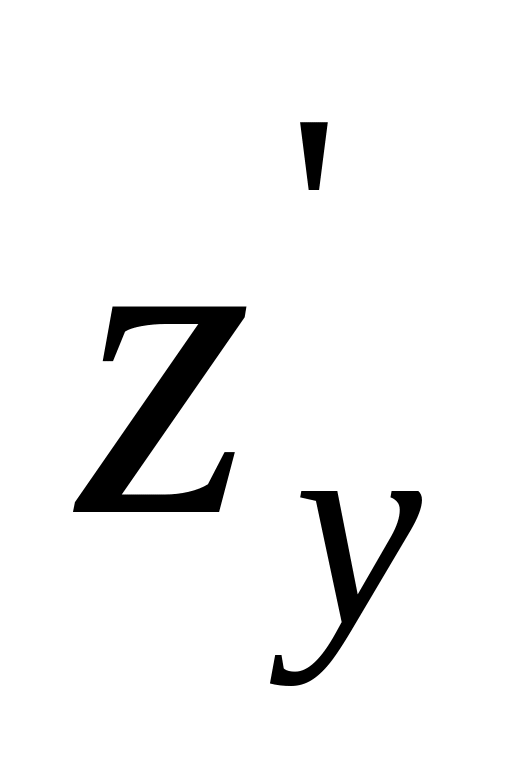 .
.Function is given. Find a partial derivative
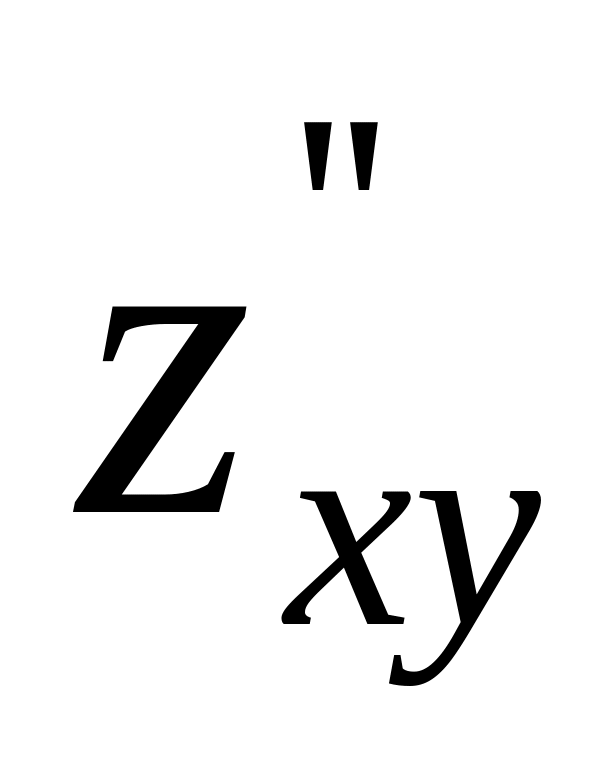 .
.Function is given. Find a partial derivative
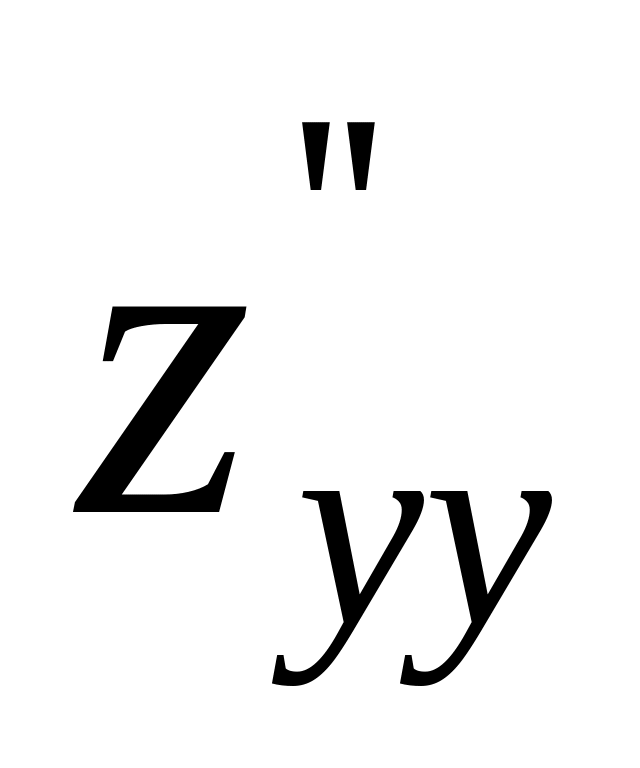 .
.Function
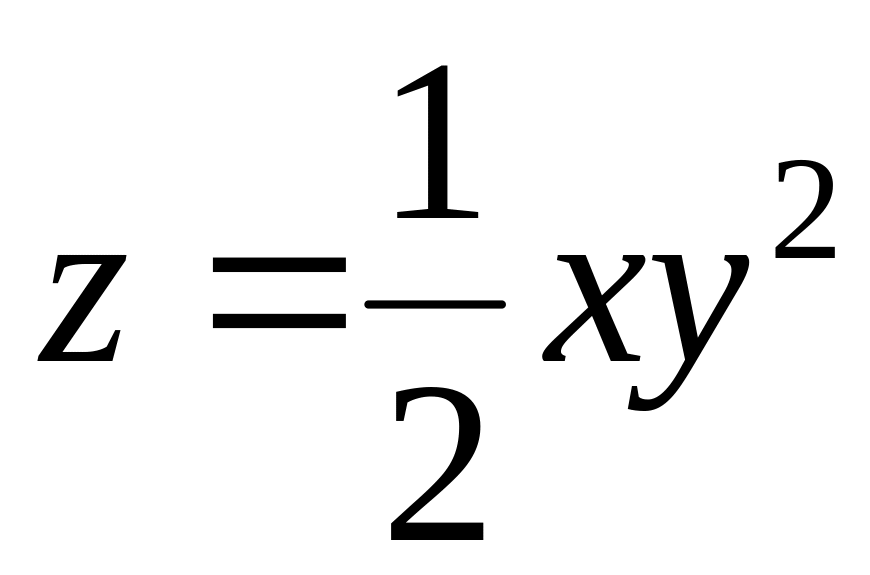 is
given. Find a partial derivative
.
is
given. Find a partial derivative
.Function
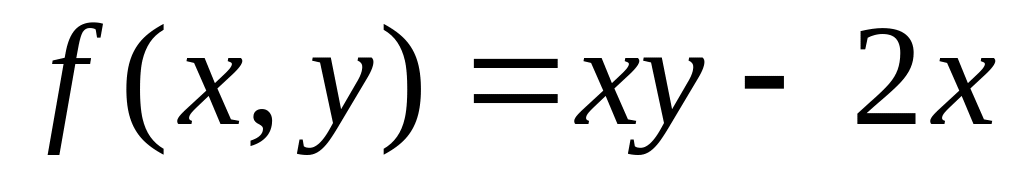 is
given. Find
is
given. Find
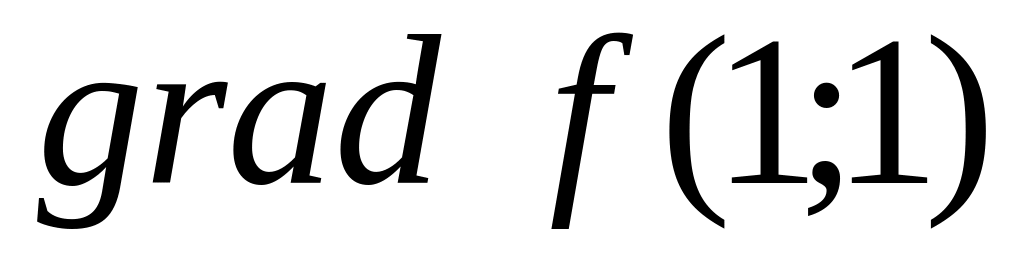 .
.Function
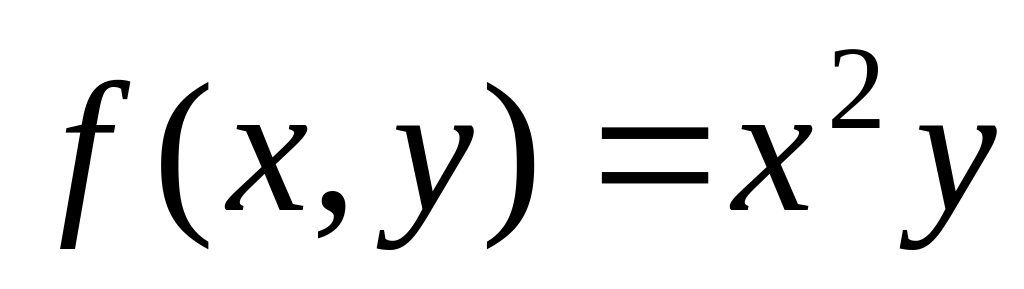 is
given. Find
is
given. Find
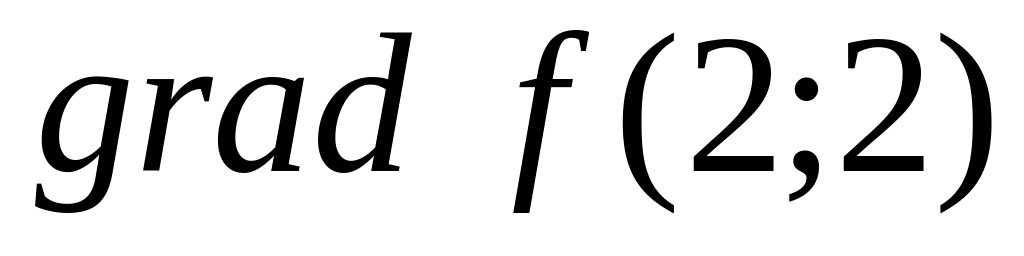 .
.Function
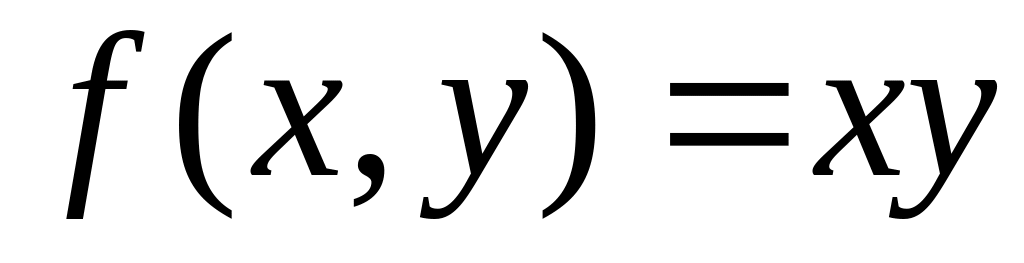 is
given. Find
is
given. Find
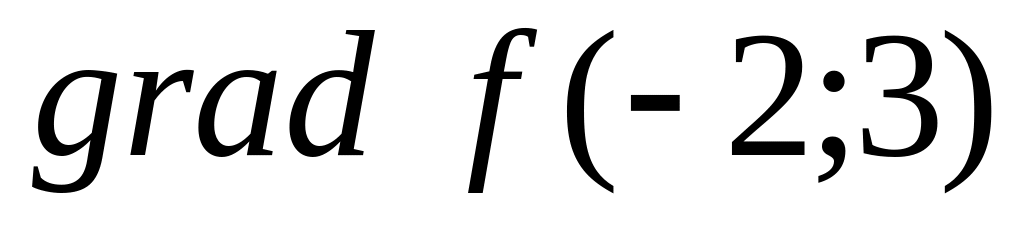 .
.Find a critical point of function .
Find a critical point of function
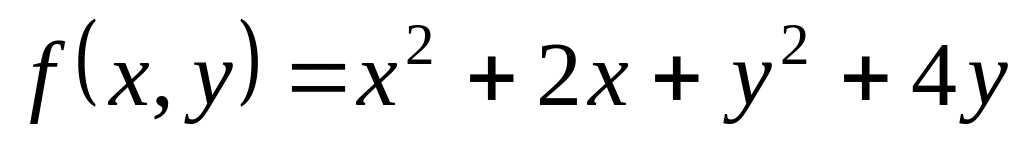 .
.Function
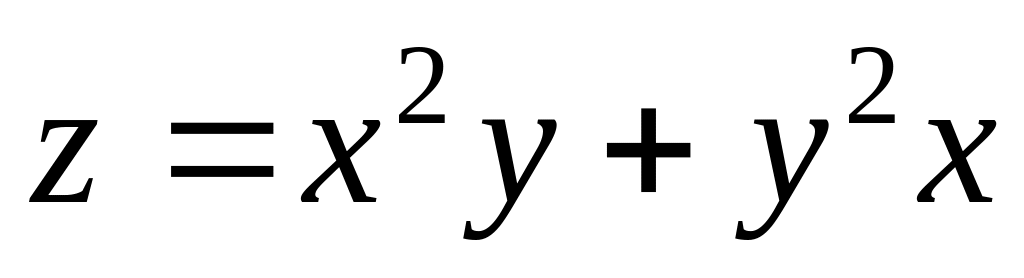 is
given. Find a partial derivative
.
is
given. Find a partial derivative
.Find the formula of total differential of function
 .
.Function
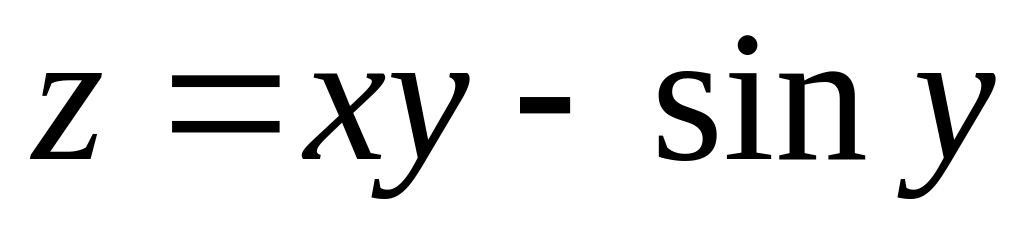 is
given. Find a partial derivative
.
is
given. Find a partial derivative
.Find a critical point of function
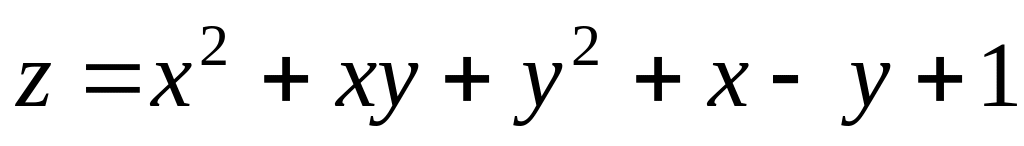 .
.Find a critical point of function
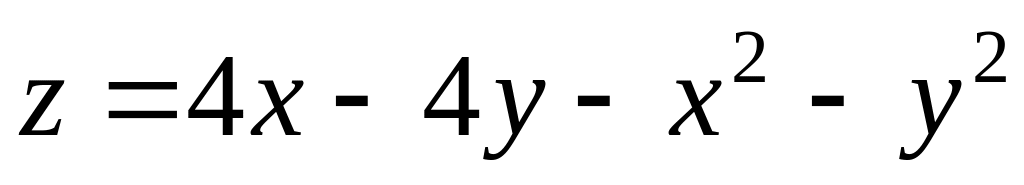 .
.Find a domain of function
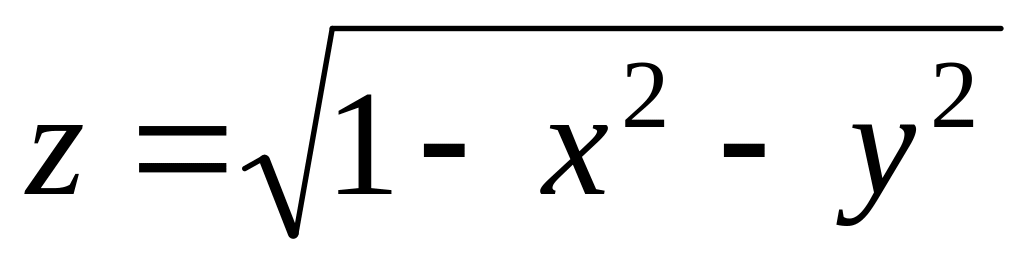 .
.Find a domain of function
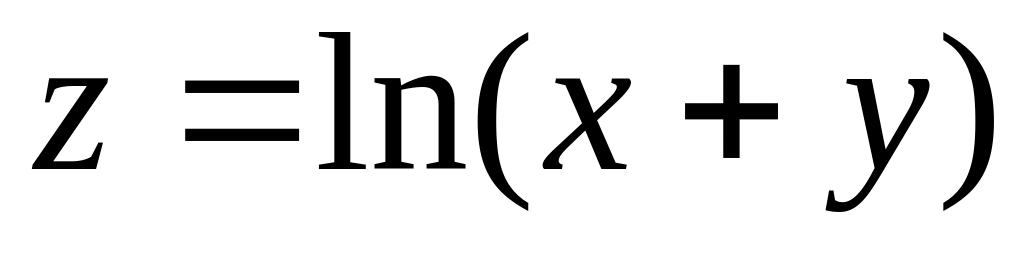 .
.Function
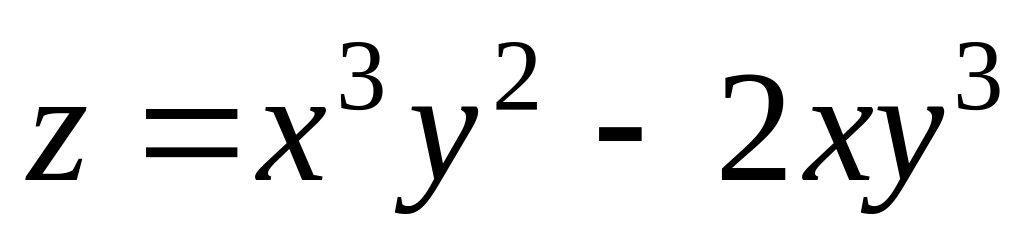 is
given. Find a partial derivative
.
is
given. Find a partial derivative
.Function
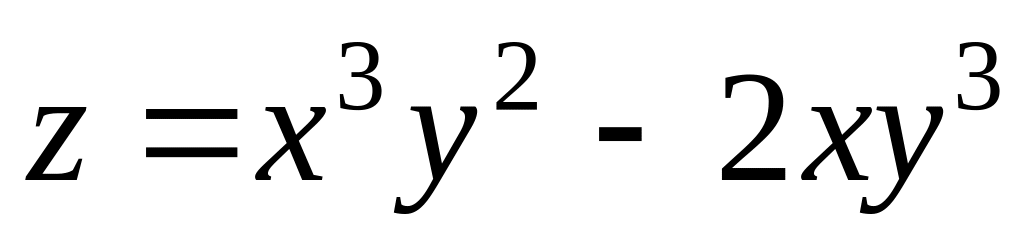 is
given. Find a partial derivative
.
is
given. Find a partial derivative
.Find total differential of function
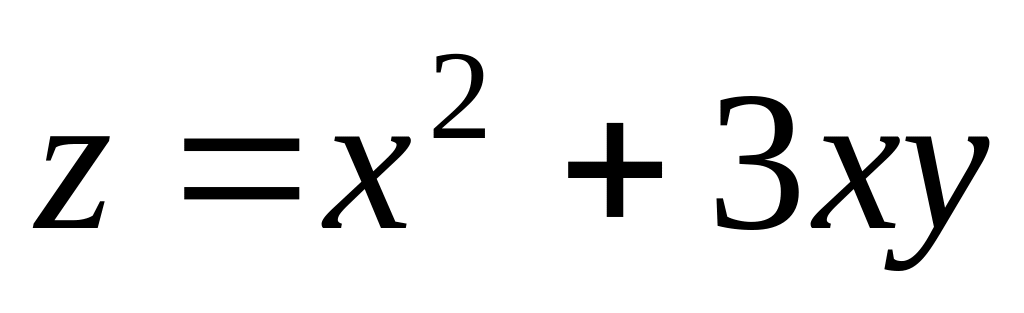 .
.Function
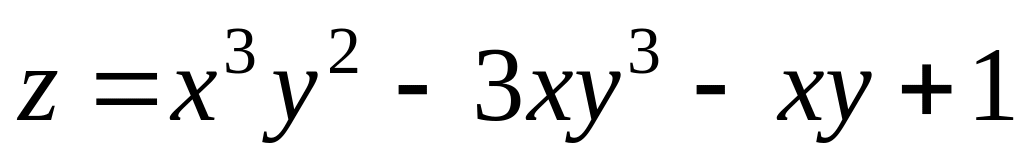 is
given. Find a partial derivative
is
given. Find a partial derivative
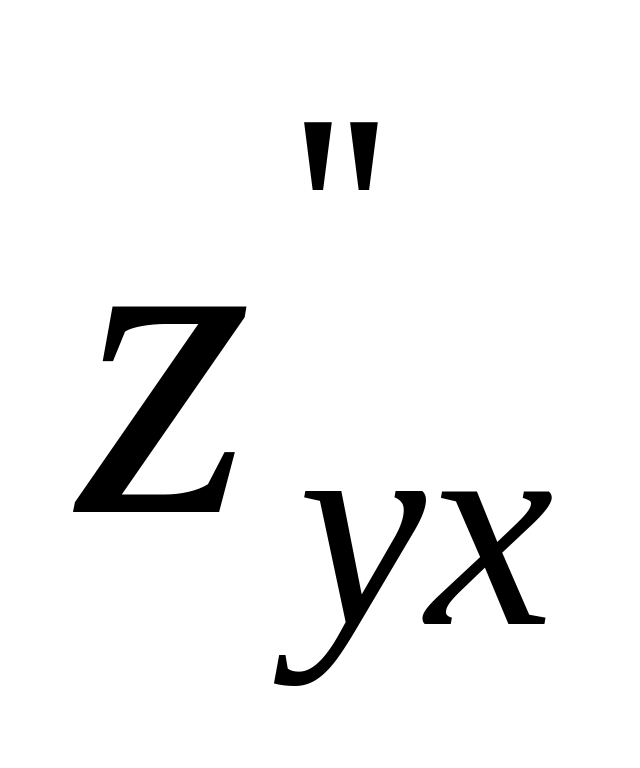 .
.
Theme 9. Antiderivative and indefinite integral
Find integral
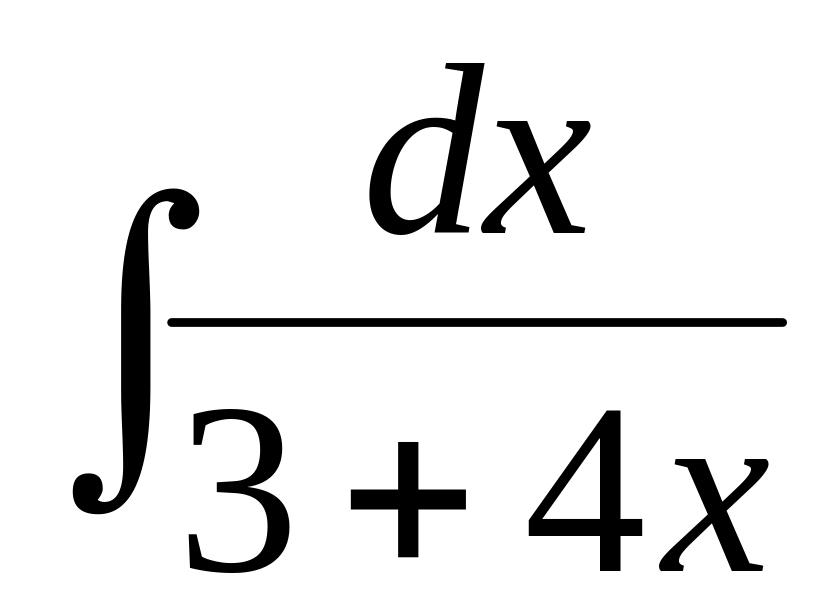 .
.Find integral
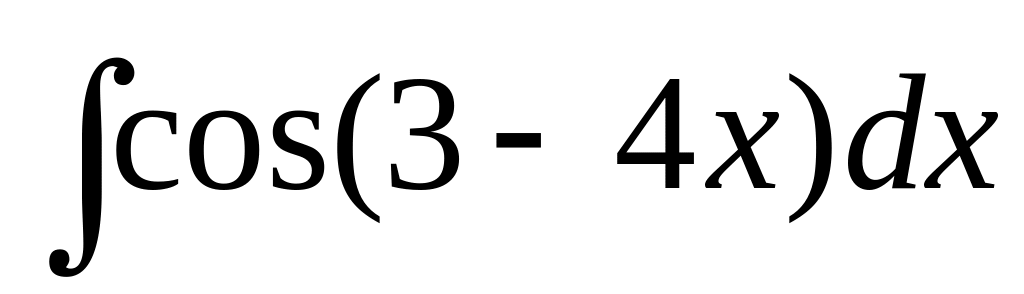 .
.Find integral
 .
.If and are differentiable functions, then
 is equal:
is equal:Find integral
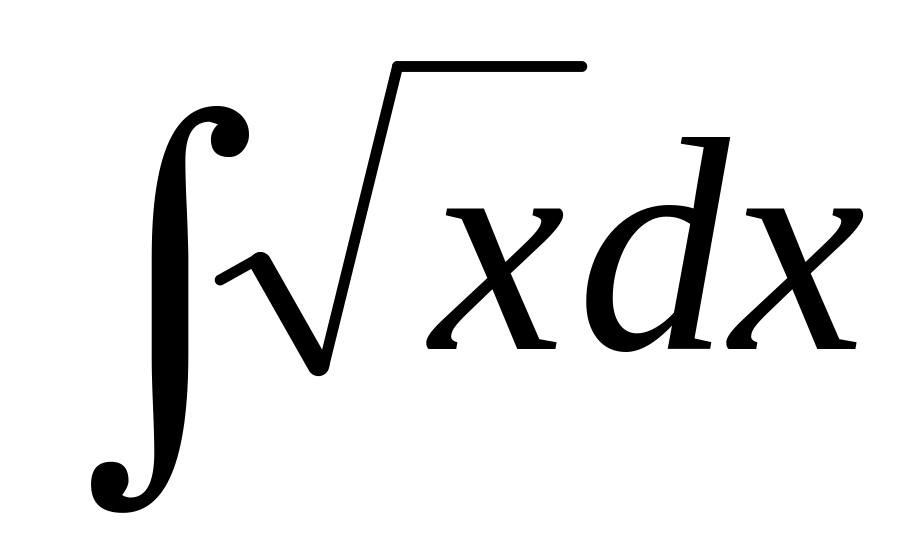 .
.Find integral
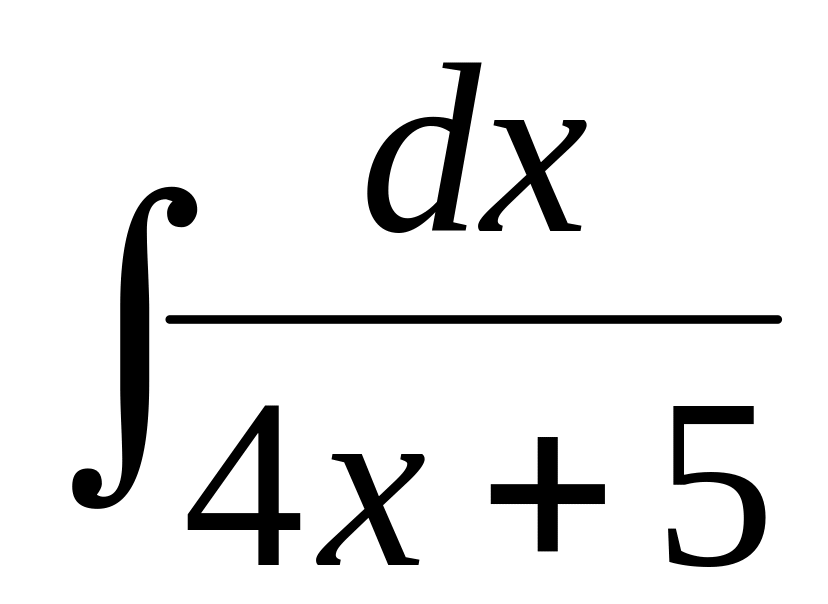 .
.Function
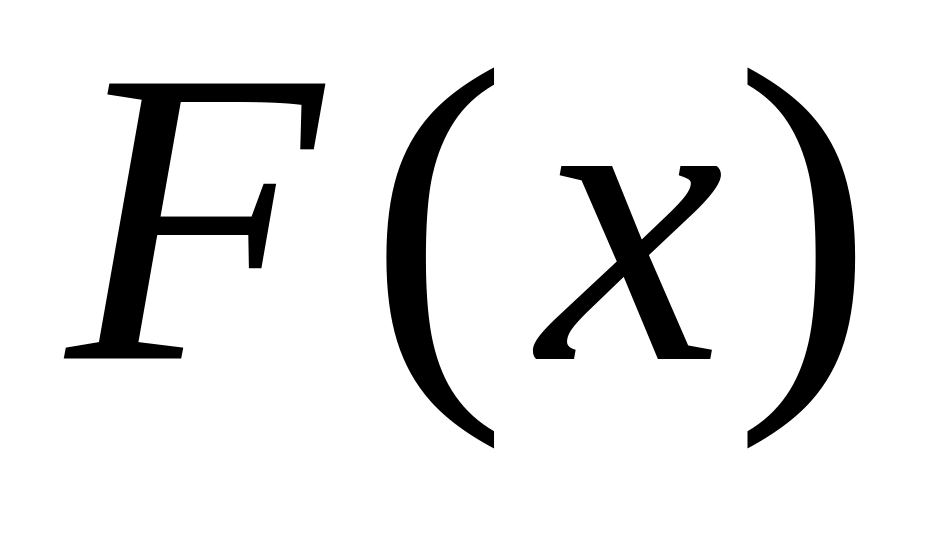 is called antiderivative
of function
is called antiderivative
of function
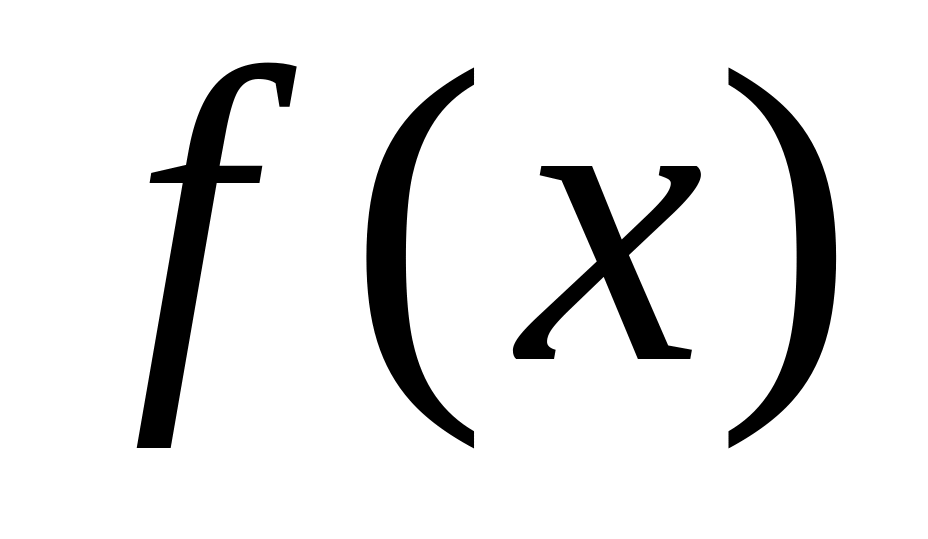 on an interval , if function
is differentiable on
and following equality is executed:
on an interval , if function
is differentiable on
and following equality is executed:Integral
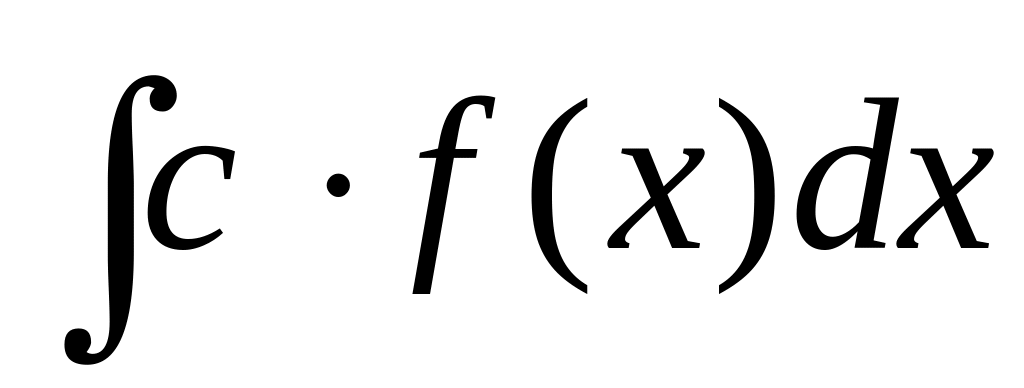 is equal:
is equal:Integral
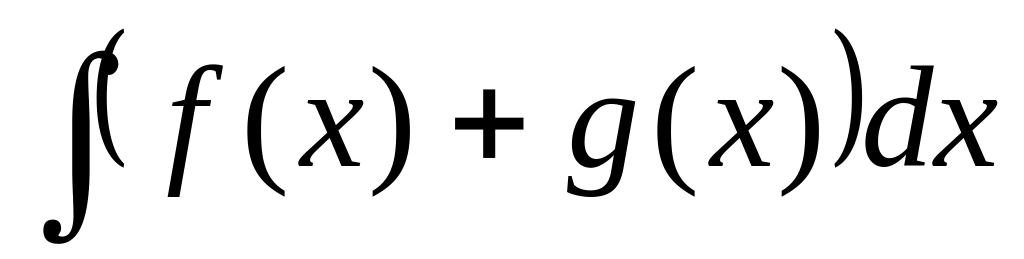 is equal:
is equal:Integral
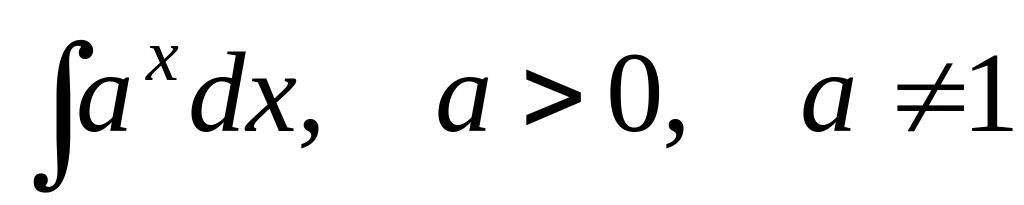 is equal:
is equal:Find expedient substitution for a finding of integral
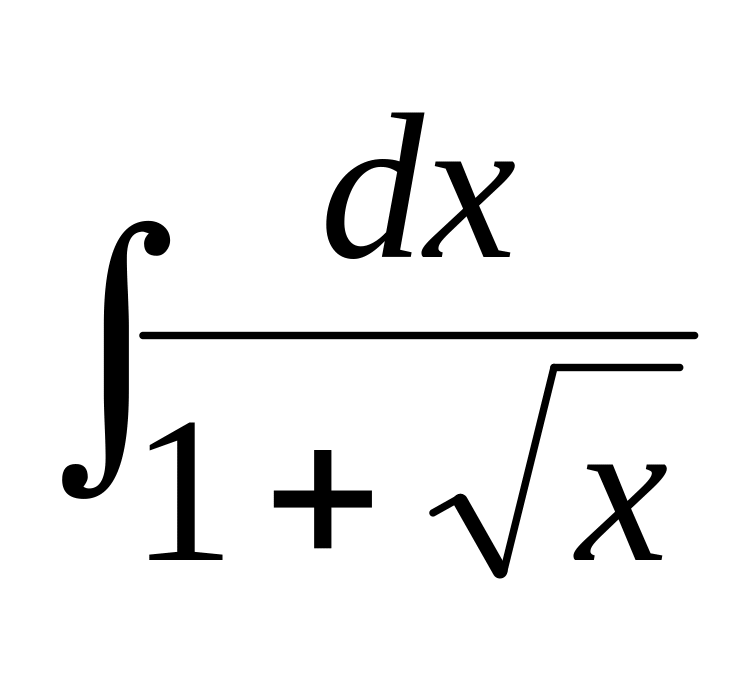 .
.Find integral
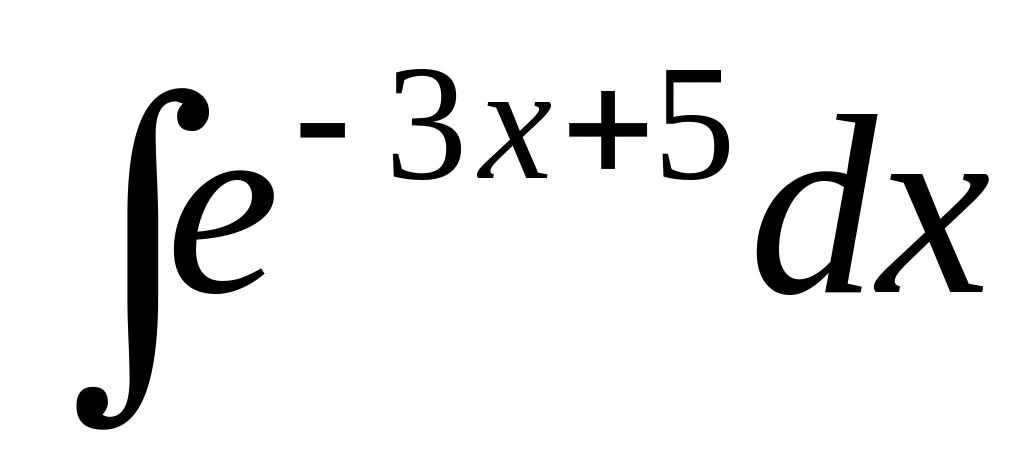 .
.Find integral
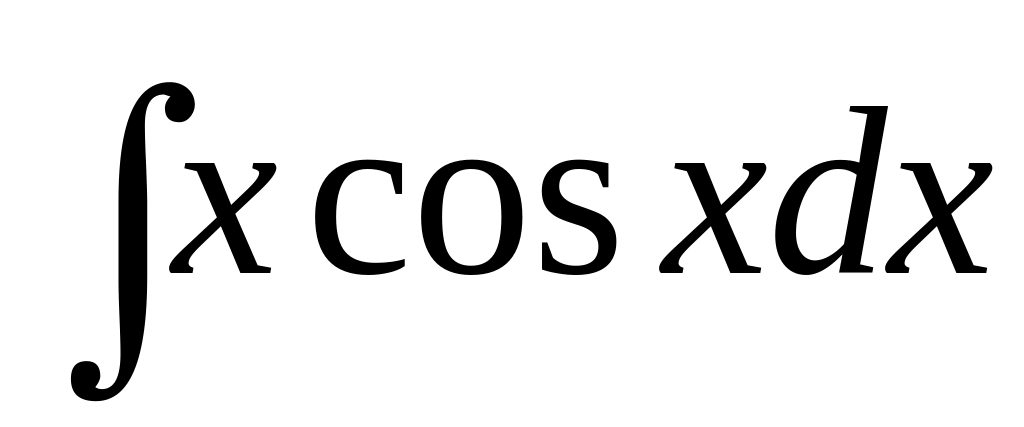 .
.Formula of integration in parts for indefinite integral is given by:
Find integral
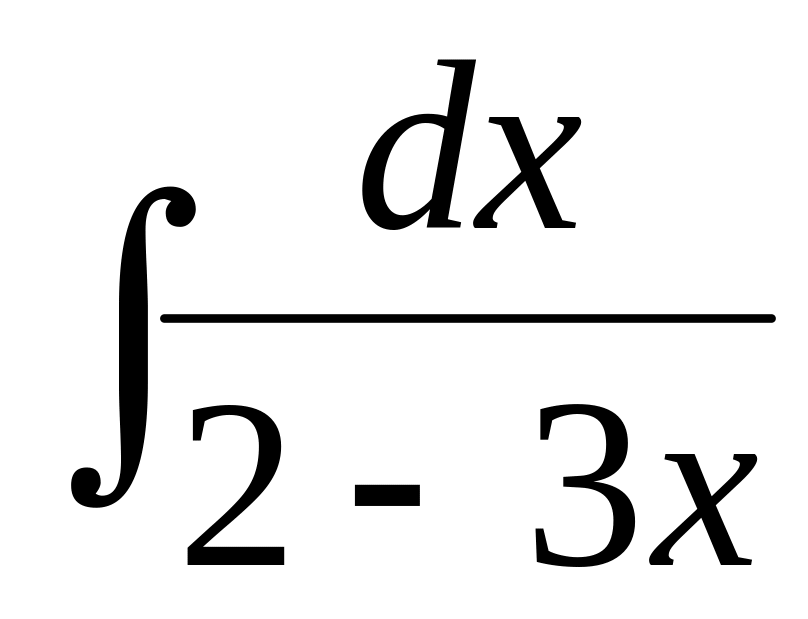 .
.Find integral
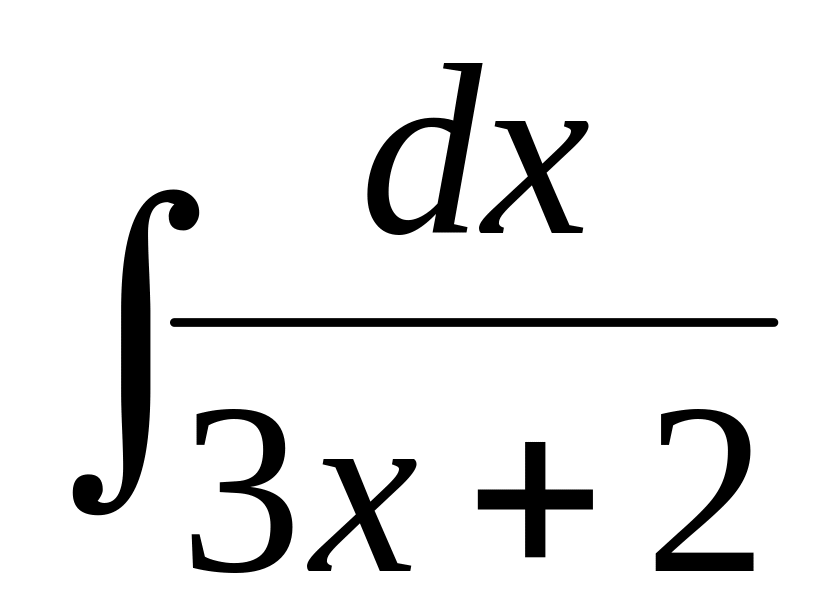 .
.Find integral
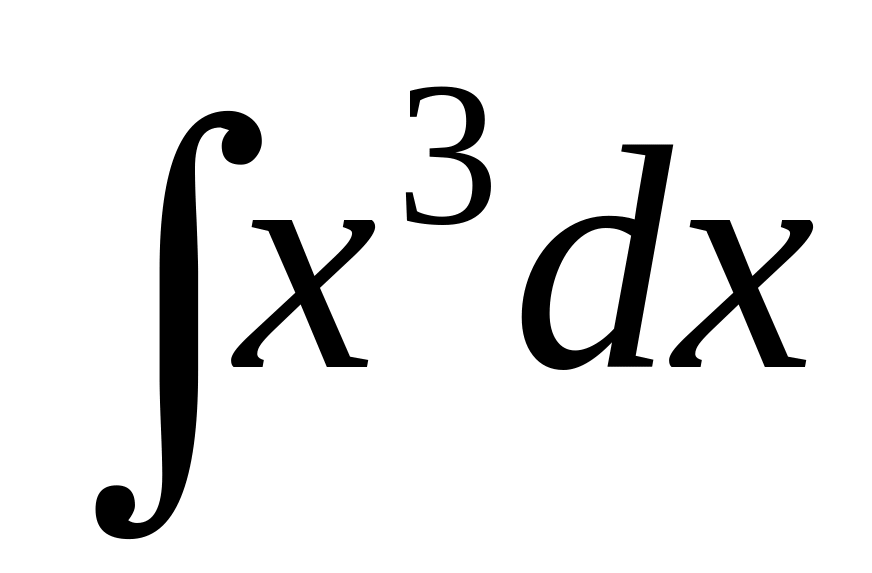 .
.Find integral
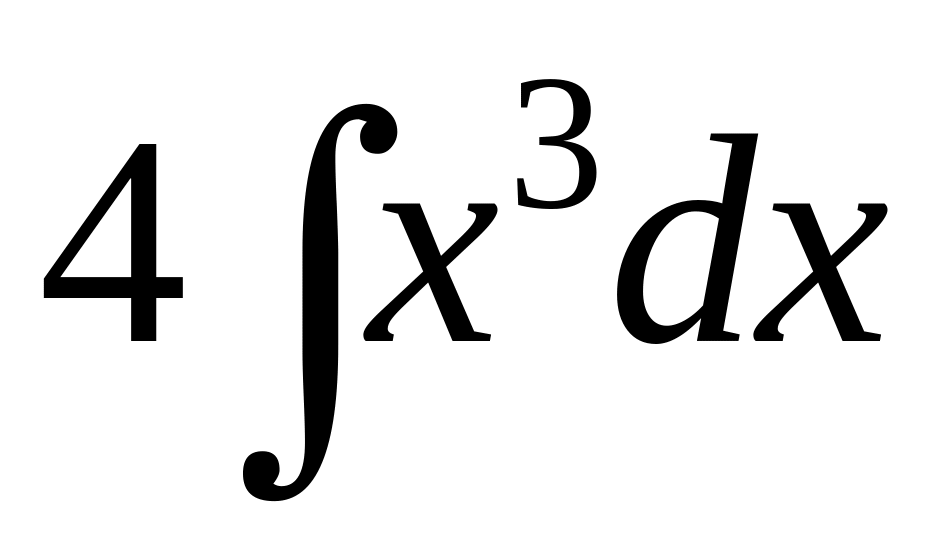 .
.Find integral
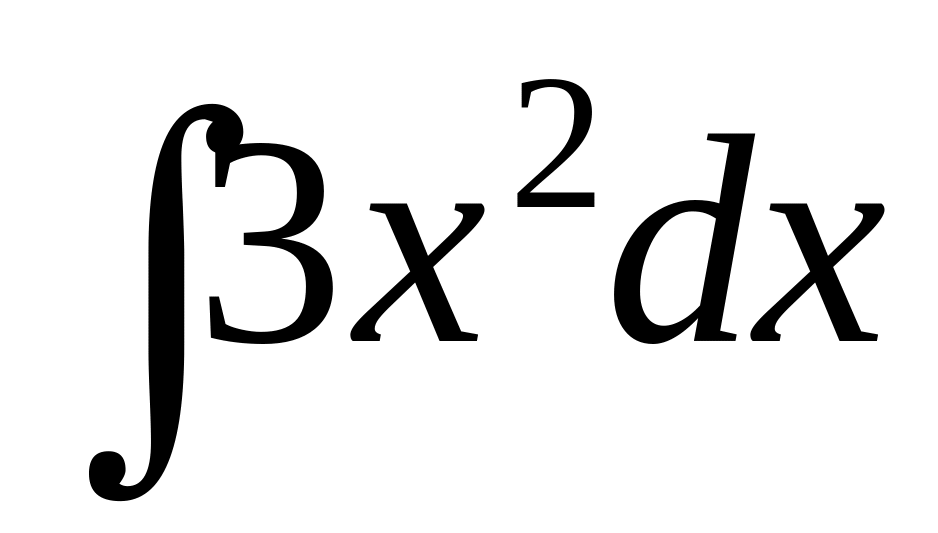 .
.Find integral
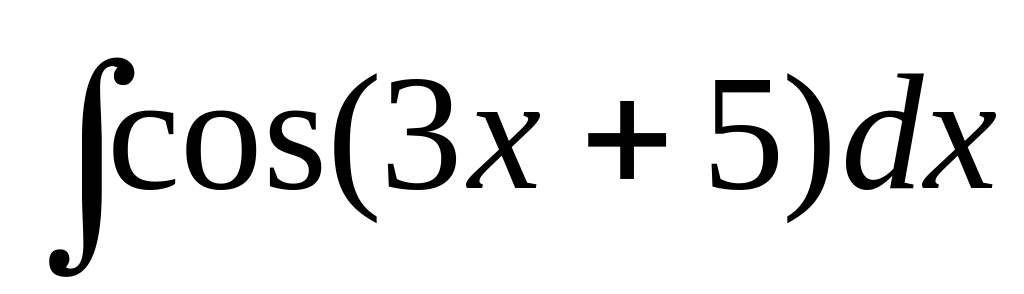 .
.Find integral
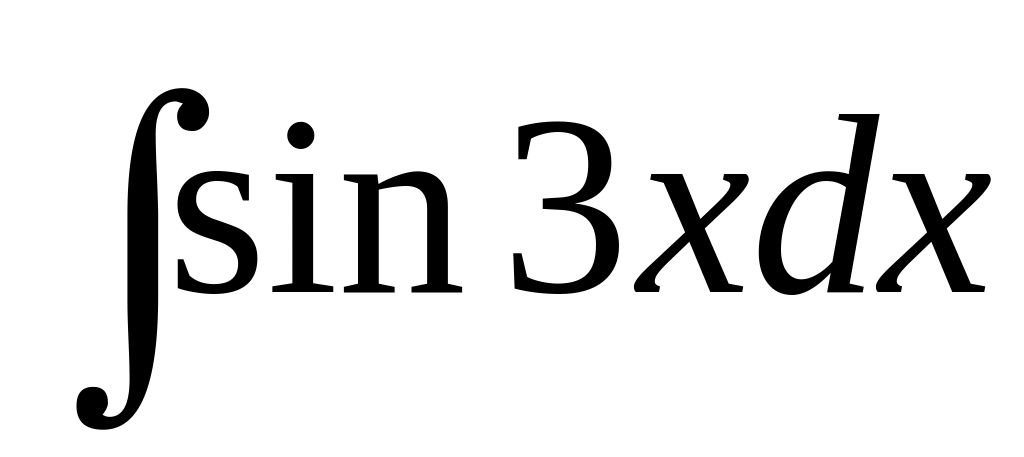 .
.Integral
 is equal:
is equal:Find integral
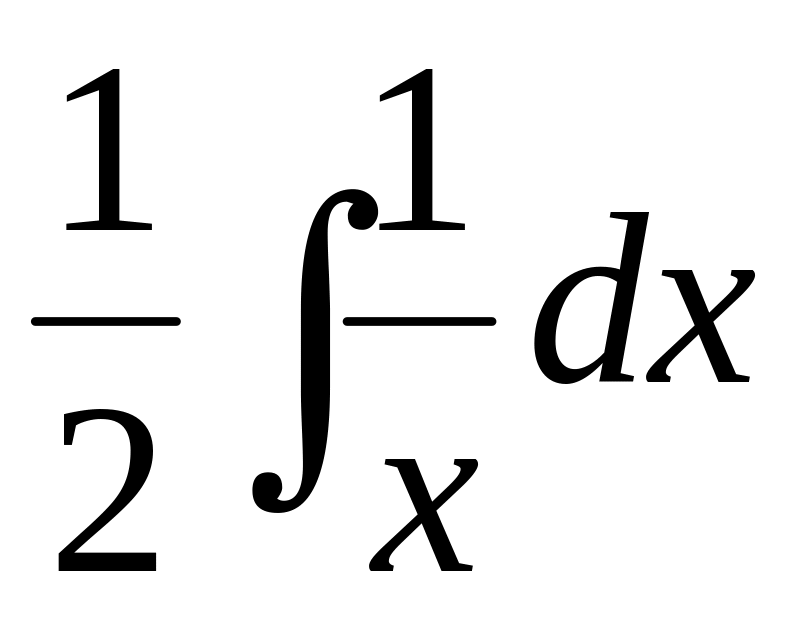 .
.Find definition of indefinite integral.
Integral
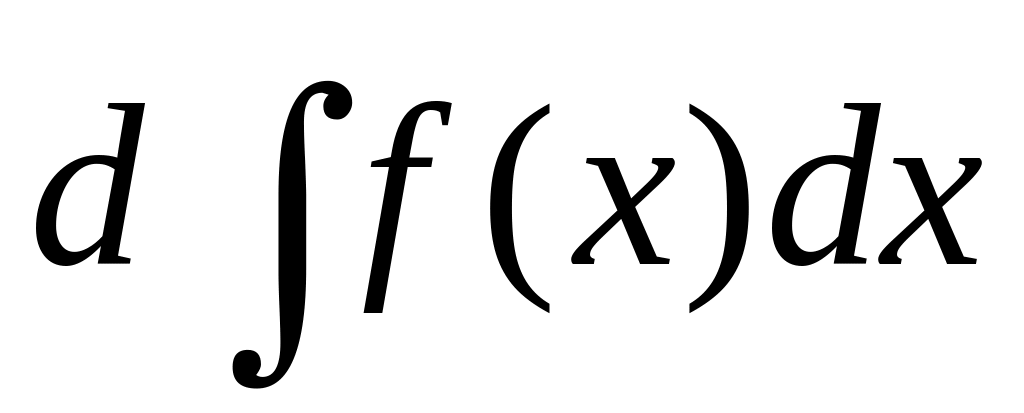 is equal:
is equal:Integral
 is equal:
is equal:Integral
 is equal:
is equal:Integral
 is equal:
is equal:Integral
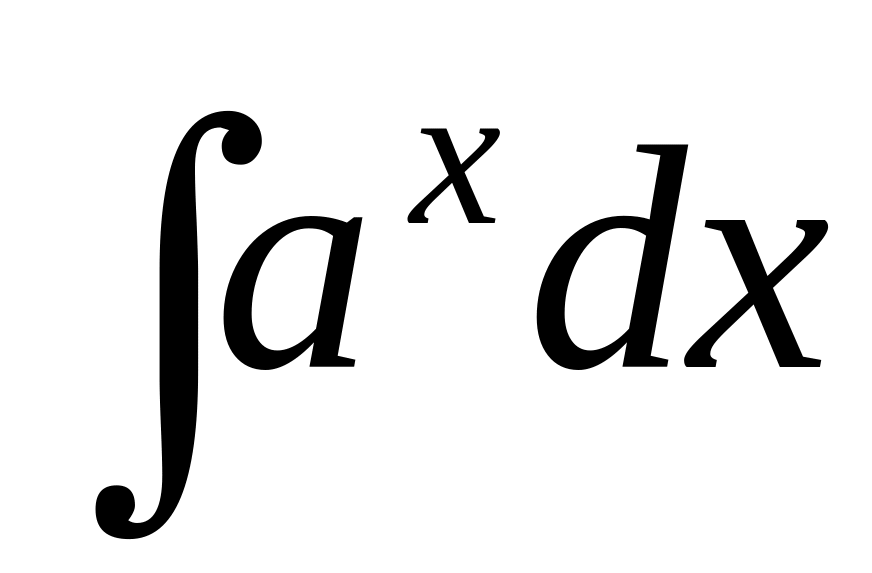 is equal:
is equal:Integral
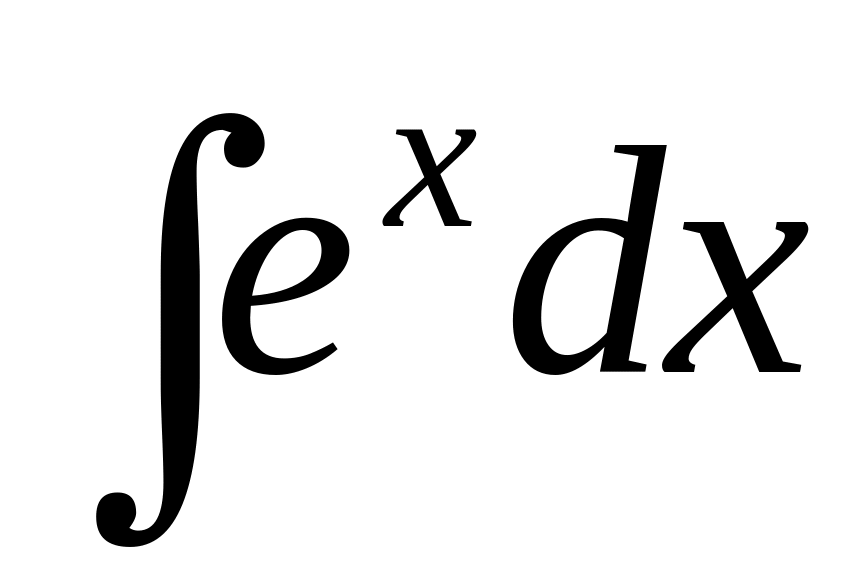 is equal:
is equal:Integral
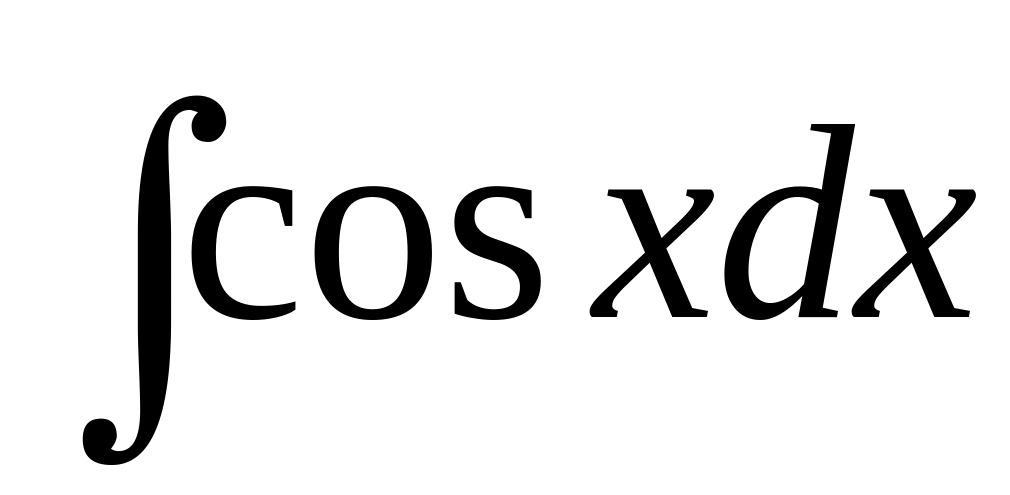 is equal:
is equal:Integral
 is equal:
is equal:Find integral
 .
.Find integral
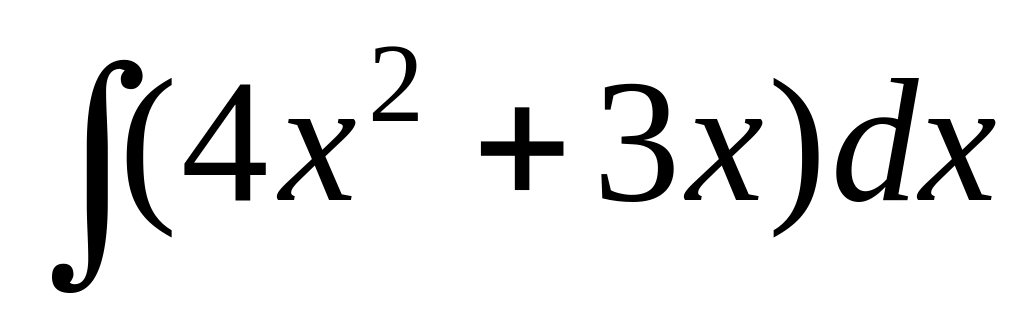 .
.Find integral
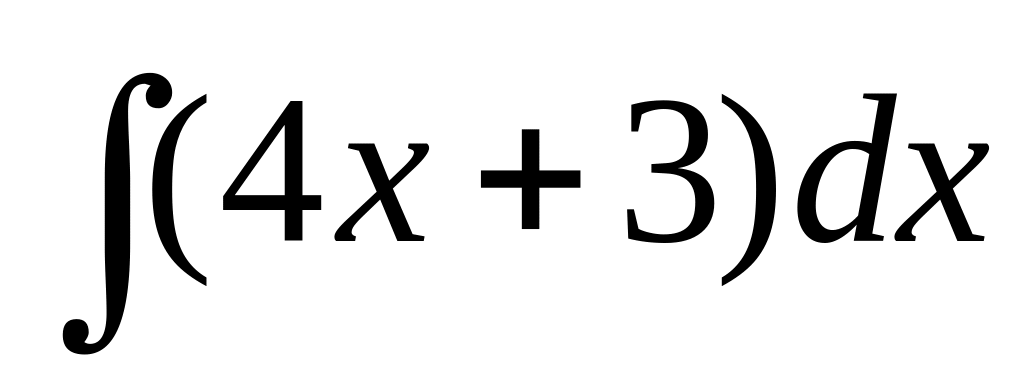 .
.Find integral
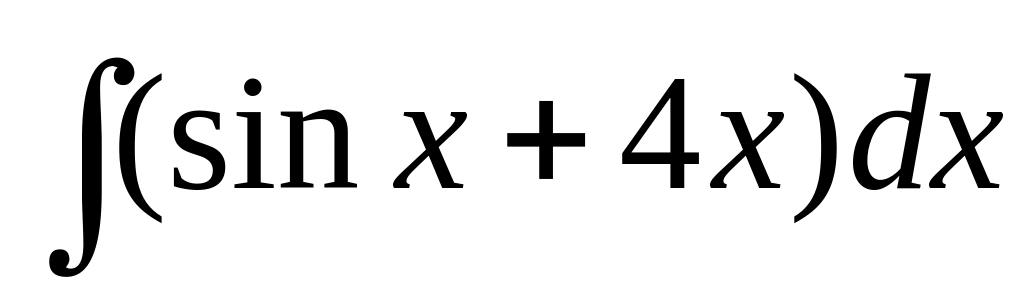 .
.Find integral
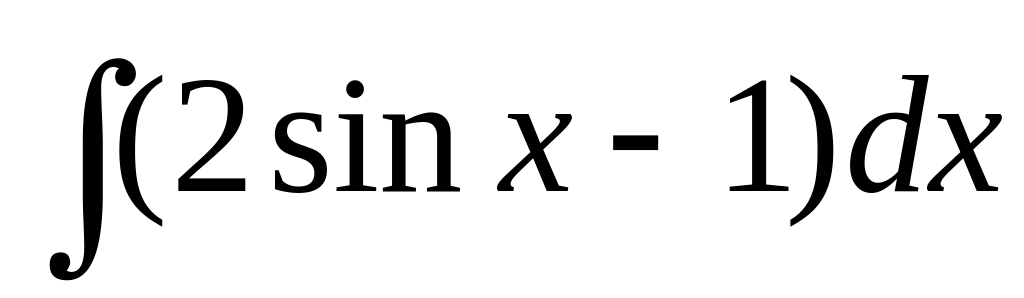 .
.Find integral
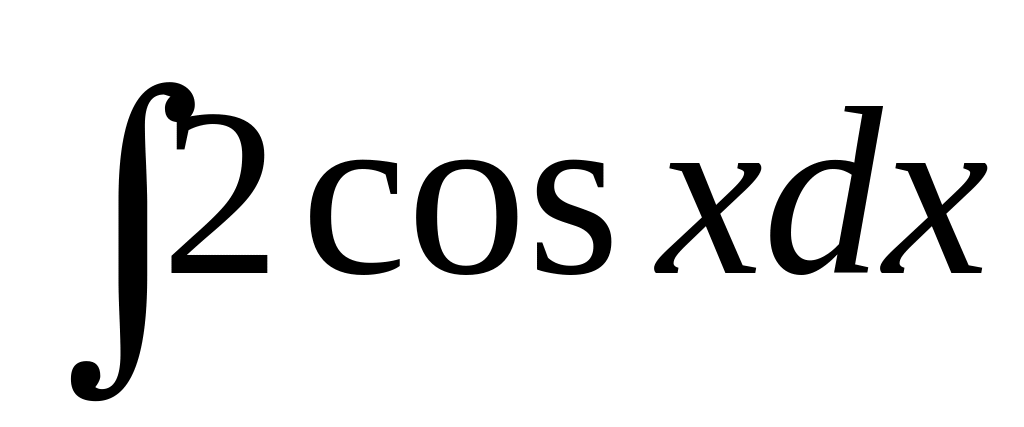 .
.
Theme 10. Definite integral and its applications
327)
Calculate integral
![]() .
.
328)
Calculate integral
![]() .
.
329)
Find geometrical meaning of the definite integral
![]() .
.
330)
Find the area of the figure, limited by a parabola
![]() and an axis using definite integral.
and an axis using definite integral.
331)
Calculate
integral
![]() .
.
332)
Calculate
integral
 .
.
333)
Calculate the area of the figure, limited by lines
![]() ,
,
![]() ,
,
![]() .
.
334)
Calculate
the area of the figure, limited by lines
,
![]() .
.
335)
Calculate the area of the figure, limited by lines
![]() ,
,
![]() ,
,
![]() .
.
336)
Calculate
improper integral
![]() or establish its divergence.
or establish its divergence.
337)
Calculate
improper integral
![]() or establish its divergence.
or establish its divergence.
338)
Calculate
improper integral
![]() or establish its divergence.
or establish its divergence.
339)
Calculate
improper integral
![]() or establish its divergence.
or establish its divergence.
340)
Calculate
improper integral
![]() or establish its divergence.
or establish its divergence.
341)
Let
function
is integrated on a segment
![]() ,
then function
,
then function
![]() also is integrated on this segment and following equality is
executed:
also is integrated on this segment and following equality is
executed:
342)
Let
functions
and
![]() are integrated on a segment
,
then function
are integrated on a segment
,
then function
![]() also is integrated on the given segment and following equality is
executed:
also is integrated on the given segment and following equality is
executed:
343) What of following equality is correct?
