11.1. Спектры периодических сигналов: одиночной гармоники, произвольного периодического сигнала, апериодического сигнала

Если читать то здесь ответ на вопрсы 11.1 по 11.4

Важным приемом, который широко используется для сжатия непрерывных сообщений, является их спектральные преобразования. Спектр – это представление зависимости в частотной области.

Наиболее прост спектр гармонической зависимости (например, синусоиды), который в координатах амплитуда-частота представляет собой линию рис.10-1. При этом ”линейной” частоте гармоники f0 = 1/T (Гц), которая равна обратной величине периода Т, соответствует “круговая” частота ω0 = 2πf0 = 2π/Т.

Рис.10.1. Гармоническая функция от времени и ее спектр

От спектра гармоники легко перейти к спектру любой периодической зависимости, поскольку, как известно, последнюю всегда можно представить как сумму гармонических составляющих, частоты которых кратны основной частоте f0 (ω0).

Пример такого подхода иллюстрирует рис.10.2, где показано построение приближения периодической последовательности импульсов амплитудой Е и длительностью Т/2 из набора гармоник с частотами ω0, 3ω0 и 5ω0. При этом спектр такой зависимости включает линии, отвечающие каждой из гармоник. Он имеет вид решетки с шагом линий равным f0 (ω0).

Рис.10.2. Пример построения приближения периодической функции как суммы гармоник

Математическое описание такого подхода выглядит так. Функция x(t) вычисляется как сумма ряда Фурье:

где ak и bk – коэффициенты ряда Фурье вычисляются по формулам (10.2):

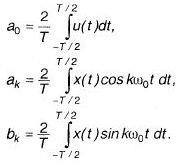
Как видно, амплитуды гармонических функций определяются исходной зависимостью x(t) в пределах одного периода от -Т/2 до T/2.

От ряда Фурье в виде (10.1) можно перейти к эквивалентному представлению (10.3)

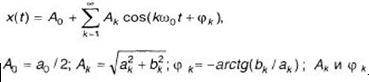
где - это, соответственно, амплитуда и начальная фаза k-той гармоники в ряде Фурье. Амплитуды гармоник образуют спектр амплитуд сигнала. Величины образуют спектр фаз сигнала.

Для абсолютно точного получения заданного сигнала, как видно из (10.1), необходимо суммировать бесконечно много гармоник. На практике берут конечное число членов ряда Фурье. Чем больше взять слагаемых, тем более точно будет получена требуемая форма сигнала.

В математике часто используют запись ряда Фурье в комплексной форме (10.4)

где - комплексные амплитуды гармоник, - мнимая единица.

Комплексная амплитуда содержит информацию как об амплитуде, так и о фазе соответствующей гармоники. Комплексная запись (10.4) компактна и удобна, но в ней присутствуют слагаемые с отрицательными значениями к, т.е. с отрицательными частотами, и слагаемые, являющиеся мнимыми числами. Однако, если подставить в (10.4) выражения для и применить формулу Эйлера , то все слагаемые с отрицательными частотами и мнимыми значениями сократятся, и получится соотношение (10.3).

Итак, спектр периодической зависимости – линейчатый. При этом шаг линий спектра равен основной частоте (обратной величине периода) функции. Спектр имеет две составляющих – амплитудную и фазовую. Первая представляет наибольший интерес, и в дальнейшем мы будем говорить в основном о ней.

Амплитуды гармоник в спектре функции однозначно определяются видом самой функции внутри периода ее изменения и вычисляются по формулам Фурье. Вычисление спектральных составляющих - ak, bk в (10.2), Ak в (10.3) или Ck в (10.4) - по исходной функции x(t) называют прямым преобразованием Фурье, а восстановление x(t) – обратным преобразованием.

На первый взгляд допущение о периодичности функции сильно сужает круг приложения рассмотренного аппарата. Ведь на практике любое сообщение, которое несет новую информацию, не может быть сведено к периодическому повторению какого-то одного фрагмента. Однако, несложный прием позволяет обойти это ограничение: мы можем независимо рассматривать отдельные фрагменты (блоки) сообщения, допуская, что в будущем они станут повторяться. Это позволяет на практике широко применять описанный подход.

На практике для нас очень важны спектры дискретизированых непрерывных сообщений (в первую очередь – звука и изображений). Напомним, что дискретизация включает фиксацию последовательности амплитуд x(n) непрерывной зависимости x(t) с периодом Tд или, что то же самое – с частотой fд = 1/ Tд (рис.10.4).

На практике всегда рассматривается конечная последовательность значений длиной N. При этом ее можно трактовать как один период полной последовательности значений, а значит – применить соответствующий аппарат вычисления спектра.

При этом спектр может состоять из N гармоник Х(k), амплитуды которых находятся по аналогии с (10.4).

Т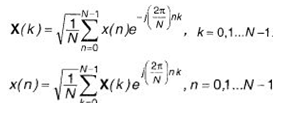 еперь прямое и обратное преобразования можно представить в виде (10.6):

Нахождение коэффициентов по (10.6а) называют прямым дискретным преобразованием Фурье (ДПФ), а получение сигнала по этим коэффициентам в соответствии с (10.6б) - обратным ДПФ. Частоте , присутствующей в членах обычного ряда Фурье и имеющей размерность рад/с, в ДПФ соответствует безразмерная величина . Отношение k/N показывает, какую часть частоты дискретизации составляет частота данной дискретной гармоники.