
Билет1 (ФНП:предел и непрерывность)
U=f(x,y)
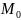 (
( )
δ-окр
)
δ-окр
Зафиксируем
у и придадим х приащение ∆х х-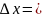 U-приращение
U-приращение
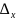 U=f(
U=f(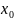 +
+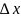 ,
,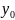 )-
f(
)
)-
f(
)
x-фикс, у-∆у=>∆yU=f( +∆y)- f( )
если же х и у получат приращение, тогда мы получим полное приращение
U=f( + , +∆у)- f( )
Опр:Число
А наз-ся пределом ф-и U(x;y)
в (.)
при стремлении точки х,у в (.) х0,у0
прооизвольным образом, если для всех
Е>0 существует ∆>0: <∆
=> f(x,y)=f(
)<E
<∆
=> f(x,y)=f(
)<E
Опр:ф-я
U=f(x,y)
называется непрерывной в точке
,
если она определена в этой точке, и ее
окрестности и
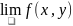 =
f(
)
=
f(
)
Опр:ф-я U непрерывна на множество Д, если она непрерывна в каждой точке этого множества
Св-ва непрерывной ф-и одного переменного без изменений переносится в данном случае
Билет2(ЧП фнп 1-го и высших порядков)
Опр:производная f( ) ф-и по переменной х в точке наз-ся ЧП по х от ф-и f(x,y) в точке
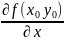 =
=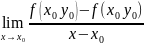
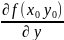 =
=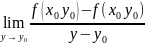
Опр:ЧП
от прозводных
 ,
,
 наз-сячп второго порядка
наз-сячп второго порядка
 (
)=
(
)=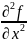
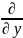 (
)=
(
)=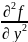
Смешанные
ЧП: Теорема: если ф-я z=f(x,y)
 и
и
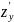 определены и непрерывны, то
определены и непрерывны, то
 =
=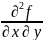 ,
т.е результат дифференцирования не
зависит от пордка дифференцирования
,
т.е результат дифференцирования не
зависит от пордка дифференцирования
ЧП порядка n это ЧП от порядка (n-1)
Билет3 (дифференциал фнп 1-го и высших порядков)
Опр:ф-я
z=f(x,y)
в точке наз-ся дифференцируемой в М(х,у),
если ее приращение в данной точке можно
представить в виде ∆z=A∆x+B∆y+ (∆x,∆y)∆x+
(∆x,∆y)∆x+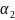 (∆x,∆y)∆y,
где АиВ то числа независящие от ∆x,∆y
соответственно
(∆x,∆y)∆y,
где АиВ то числа независящие от ∆x,∆y
соответственно
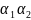 -это
БМВ
-это
БМВ
Дифференциалом ф-ии I-го порядка наз-ся гл.линейная часть е приращения. Это выражение так же наз-ся полным дифференциалом ф-ии z.
∆z=A∆x+B∆y-полный дифференциал
Т:если
ф-я z=f(x,y)
дифференциуема в точке (х,у), то z
имеет ЧП и А=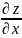 (x,y)
(x,y)
B=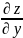 (x,y)
(x,y)
dz= dx+ dy
Т2:если ф-я z дифференцируема в точке (х,у), то она непрерывна в данной точке
Опр:полным
дифференциалом 2-го порядка ф-и z
наз-ся дифференциал ее дифференциала
1-го порядка т.е
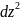 =d(dz)
=d(dz)
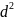 z=
z=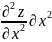 +2
+2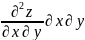 +
+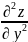 ∂
∂
 z=
z=
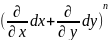 (z)
(z)
Билет4(дифференцирование сложных фнп(с док-вом), дифференциал сложной фнп)
Теорема:Если
ф-ии x(t),
y(t) – диф-мы
в точке t, а ф-я U
– диф-ма вв точке (х,у), то ф-я U=(x(t);у(t))
диф-ма в точке t и
 =
=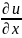 *
*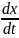 +
+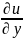 *
*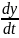 =
=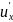 *
* +
+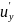 *
*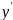
Док-во:
Пусть z=z(x,y), где x=x(u,v), y=y(u,v)
 =
=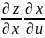 +
+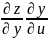
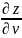 =
=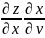 +
+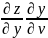
Правило: производная от сложной ф-ии по каждой независимой переменной, есть сумма произведений. ЧП по всем ее промежуточным переменным на производные последних по независимой переменной
Теорема(инвариантность формы полного дифференциала сложной фнп)
Пусть ф-я z=z(u,v), где u=u(x,y) v=v(x,y) => dz= du+ dv
Док-во т.к z=z(u(x,y);v(x,y))=z(x,y) тогда dz= dz= dx+ dy
=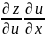 +
+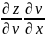
=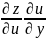 +
+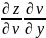
dz= +
)dx+(
=
+
)dy=
+
)dx+(
=
+
)dy=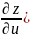 +
dy)+
(
+
dy)+
( dx+
dx+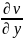 dy)=
dy)=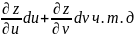
Билет5 (производная неявной фнп)
Теорема
если ур-ие F(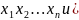 обращается в тождество в точке (
обращается в тождество в точке ( и если в некоторой окрестности этой
точки ф-я F непрерывна и
имеет непрерывные ЧП при этом
и если в некоторой окрестности этой
точки ф-я F непрерывна и
имеет непрерывные ЧП при этом
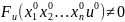 то данное ур-ие имеет в окрестности этой
точки единственное решение u=f(
то данное ур-ие имеет в окрестности этой
точки единственное решение u=f(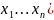 .
При этом ф-я F(
непрерывна
и имеет непрерывные ЧП
.
При этом ф-я F(
непрерывна
и имеет непрерывные ЧП
Док-во:
пусть условие этой теоремы выполнены
=) подставляя вместо переменной U
ф-ию f получаем тождество
F( =)полный дифференциал ф-ии F
будет равен 0. dF(
=)полный дифференциал ф-ии F
будет равен 0. dF(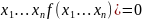 т.е
т.е
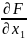 dx+
dx+ d
d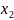 +…+
+…+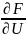 du=0
=) dU=(
/(-
du=0
=) dU=(
/(-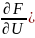 )dx+(
)dx+(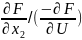 )d
+…+(
)d
+…+(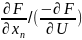 )d
)d
dz=
d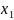 +
d
+
d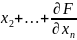 d
d
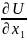 =-
=- …
…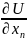 =
=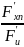
1)F(x,y)=0;
т.е y=y(x)
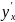 =-
=-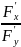
2)F(x,y.z)=0
т.е z=z(x,y,z)
=-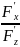 =-
=-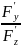
Билет6(экстремум фнп. Наибольшие и наименьшие значения фнп по замкнутой области)
Опр:
Если для функции z
= f(x,
y),
определенной в некоторой области, в
некоторой окрестности точки М0(х0,
у0)
верно неравенство![]() ,
то точка М0
называется точкой
максимума.
,
то точка М0
называется точкой
максимума.
Опр:
Если для функции z
= f(x,
y),
определенной в некоторой области, в
некоторой окрестности точки М0(х0,
у0)
верно неравенство
![]() ,
то точка М0
называется точкой
минимума
,
то точка М0
называется точкой
минимума
Т: Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области D функция z(x,y) достигает своего наибольшего M и наименьшего m значений.
Можно предложить следующий план нахождения M и m. 1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы. 2. Находим стационарные точки внутри D. 3. Находим стационарные точки на каждой из границ. 4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения.
Билет7(двойные интегралы:опр, их св-ва и вычисления)
Определение двойного интеграла
Пусть в некоторой области D на координатной плоскости XOY определена функция двух переменных z = f (x, y). Предполагается, что граница области D состоит из конечного числа кривых, заданных уравнениями вида y = f (x) или x = φ (y), где f (x) и φ (y) – непрерывные функции.
Разобьем область D на бесконечно малые ячейки прямыми, параллельными координатным осям.
В каждой ячейке выберем точку Ci,j(xi, yj).
Вычислим значения f (xi, yj) функции в этой точке.
Эти значения f (xi, yj) умножим на площади ячеек, из которых бралась точка: f (xi, yj)·Δ xi·Δ yj.
Все эти произведения сложим:
![]() .
.
Полученная сумма называется двойной интегральной суммой.
Назовем диаметром d(D) области D наибольшее расстояние между точками этой области. Обозначим через λ наибольший из диаметров частичных областей Di
![]() .
.
О п р е д е л е н и е. Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит от способа разбиения области D, от способа выбора точек Ci,j (xi, yj) внутри каждой ячейки
![]() .
.
В этом случае функция f (x, y) называется подынтегральной, D — областью интегрирования, x и y — переменными интегрирования, ds (или dx·dy) – элементом площади. Мы предполагаем, что функция f (x, y) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т.е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате
{ (x, y) | 0 ≤ x ≤ 1; 0 ≤ y ≤ 1}
следующим образом:
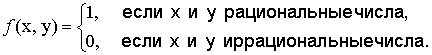
Т 1. Функция f (x, y), непрерывная в замкнутой ограниченной области D, интегрируема в этой области. Т2. Функция f (x, y),ограниченная в замкнутой ограниченной области D и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида y = ψ(x) или x = φ (y), интегрируема в этой области.
Вычисление площади плоской фигуры двойным интегралом
Если положить f (x, y) = 1 всюду в области D, то непосредственно из определения двойного интеграла получим выражение площади s области D в виде двойного интеграла:
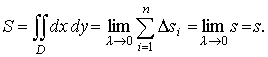
Свойства двойных интегралов
Линейное свойство
![]() .
.
Если функции f (x, y) и g(x, y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и
![]()
Аддитивное свойство по области интегрирования
![]() .
.
Теорема о среднем. Если функция f (x, y) непрерывна в области D, то в этой области найдется такая точка ( ξ; μ), что
![]() ,
,
где s — площадь фигуры D.
Билет8(тройные интегралы:опр, их св-ва и вычисления)
Билет9(замена переменных в кратных интегралах)
Замена переменных в кратных интегралах.
В
математическом
анализе кратным или многократным
интегралом называют множество интегралов,
взятых от
![]() переменных.
Например:
переменных.
Например:
![]()
Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число.
В двойных интегралах.
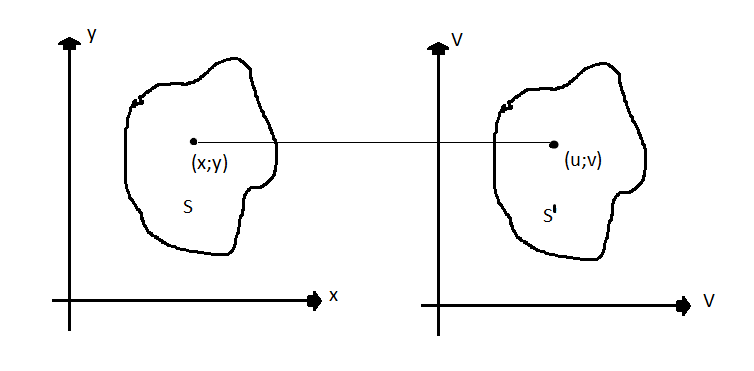
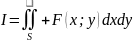
Ф-ии х; у однозначные и непрерывные на S.
Пусть
 x=x(u;v)
y=y(u;v)
x=x(u;v)
y=y(u;v)
При
замене «х» и «у» на «u»
и «v»
область S
переходит в S’,
тогда
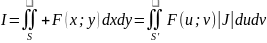
Где
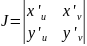
Для двойных интегралов часто используется переход от декартовых к полярным координатам
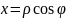
 тогда
тогда

 Переход
от декартовых координат к полярным
целесообразен, если область
интегрирования-часть круга.
Переход
от декартовых координат к полярным
целесообразен, если область
интегрирования-часть круга.
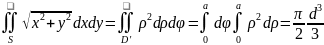
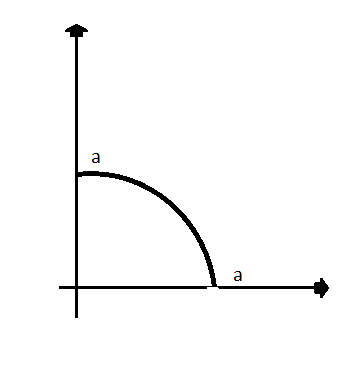
В тройных интегралах
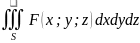
Пусть x=x(u;v;w) y=y(u;v;w) z=z(u;v;w) -однозначны и непрерывны, вместе с ЧП на области S


Наиболее распр. заменами в тройном интеграле являются:
Переход к цилиндрическим координатам:
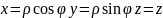
Переход к цилиндрическим координатам целесообразен, если область интегрирования-часть циллинра, или сечения плоскостями, параллельными одной из координатных плоскостей есть часть круга, или круг
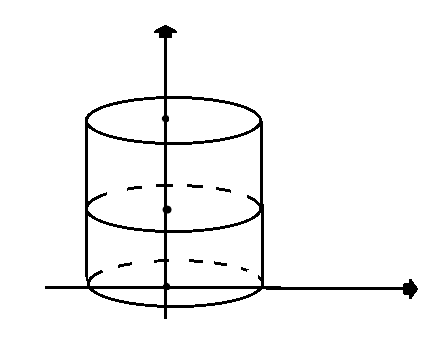
Переход к сферическим координатам

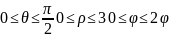
Переход к сферическим координатам целесообразен, если область интегрирования-часть шара
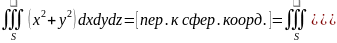
Билет10(криволинейные интегралы 1 род
Билет11(криволинейные интегралы 2 рода)
Билет12(криволинейные интегралы по замкнутому контуру)
+ 12)Криволинейные интегралы по замкнутому контуру. Формула Грина
Т еорема:Если область D, ограниченную замкнутой линией L, разбить на две части D1 и D2, то криволинейный интеграл по всей линии L равен сумме интегралов,взятых в том же направлении по линиям L1 и L2, ограничиввающим области D1 и D2.
Формула
Грина:-формула, связывающая криволинейный
интеграл по замкнутому контуру с двойным
и нтегралом,распространеным по
области,ограниченной этим контуром.
Теорема: Е сли функции Р(х,у) и Q(х,у)
непрерывны вместе со своими частными
производными первого порядка в области
D, то имеет место формула: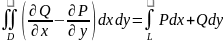 ,
где L- граница области D
и интегрирование вдоль L
производится в положительном направлении.
Доказательство:Сначала возьмем в
плоскости Оху область D,
ограниченную линией L,
пересекающейся с прямыми, параллельными
осям координат, не более чем в двух
точках. Преобразуем двойной интеграл:
,
где L- граница области D
и интегрирование вдоль L
производится в положительном направлении.
Доказательство:Сначала возьмем в
плоскости Оху область D,
ограниченную линией L,
пересекающейся с прямыми, параллельными
осям координат, не более чем в двух
точках. Преобразуем двойной интеграл: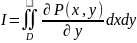 /
интегрируем сначала по х,потом по у:
/
интегрируем сначала по х,потом по у:
 .выполнив
внутреннее интегрирование, получим:
.выполнив
внутреннее интегрирование, получим: .
Во втором интеграле мы изменили пределы
интегрирования соответственно поэтому
изменился и знак. первый интеграл есть
есть нечто иное,как криволинейный
интеграл
.
Во втором интеграле мы изменили пределы
интегрирования соответственно поэтому
изменился и знак. первый интеграл есть
есть нечто иное,как криволинейный
интеграл
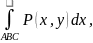 а
второй-
а
второй-
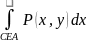 .
Сумма эт их интегралов будет криволинейным
интегралов будет криволинейным интегралом
по всему контуру L,
обходимому в отрицательном направлении.
следовательно,
.
Сумма эт их интегралов будет криволинейным
интегралов будет криволинейным интегралом
по всему контуру L,
обходимому в отрицательном направлении.
следовательно, .
Совершенно аналогично
.
Совершенно аналогично
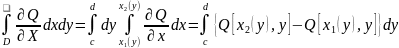 ,
где х1 (у)и х2(у)- уравнение
линий ЕАС и ЕСВ в форме, разрешенной
относительно х. рассуждая так же, как и
в первом случае, получим
,
где х1 (у)и х2(у)- уравнение
линий ЕАС и ЕСВ в форме, разрешенной
относительно х. рассуждая так же, как и
в первом случае, получим
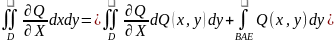 /
сумму интегралов, стоящих в правой части
последнего равенства, заменим одним
интегралом по всему контуру L,
обходимому уже в положительном
направлении:
/
сумму интегралов, стоящих в правой части
последнего равенства, заменим одним
интегралом по всему контуру L,
обходимому уже в положительном
направлении:
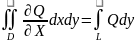 .
Вычитывая из этого равенства, получчаеи:
.
чтд
.
Вычитывая из этого равенства, получчаеи:
.
чтд
Билет13(независимость криволинейного интеграла от линии интегрирования)
Билет14(числовые ряды:св-ва сходящихся рядов)
14) Числовые ряды: свойства сходящихся рядов (с док-вом)
Пусть ![]() - последовательность чисел.
- последовательность чисел.
Определение. Если
существует ![]() ,
то говорят, что сходится бесконечный
ряд
,
то говорят, что сходится бесконечный
ряд ![]()
Если же предела не существует или же бесконечен ,то говорят, что ряд расходиться.
Свойства сходящихся рядов:
! ряд
1
![]() сходиться,
т.е
сходиться,
т.е

Если ряд 1 сходиться и с-произв. const, то
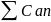 -
сходиться
-
сходиться
Пусть
 ,
тогда
,
тогда +
+
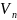 )
сходиться и его сумма =
)
сходиться и его сумма =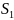 +
+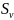
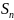 =(
=(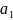 +
+ )+…+(
)+…+(
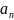 +
+
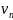 )=
(
+…
+
)
+…+ (
+
)
)=
(
+…
+
)
+…+ (
+
)
Определение:
если в ряде 1 n-первых
членов, то ряд
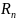 -
-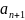 +..
=
+..
=
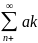
Если ряд 1 сходиться, то
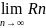 =0
=0
=
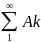 =
+
->
=S-
->
=
+
->
=S-
->
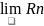 =
=
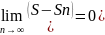
На сходимость ряда не влияет отбрасывание конечного числа его членов.
Следствие. (Необходимый признак сходимости ряда).
![]() .
Действительно, при
.
Действительно, при ![]() получаем
неравенство
получаем
неравенство ![]() ,
выполняющееся
,
выполняющееся ![]() .
Это значит, что
.
Это значит, что ![]() .
Согласно этому следствию, мы получаем
новое доказательство того, что
ряд
.
Согласно этому следствию, мы получаем
новое доказательство того, что
ряд ![]() расходится
при
расходится
при ![]() .
.
Билет15(числовые ряды с «+» членам:признаки сходимости)
Билет16(числовые ряды с «+» членами:необходимый признак. Гармонический ряд)
Билет17(числовые ряды с «+» членами:признаки сранения)
билет18(числовые ряды с «+» членами:признак Даламбер)
Числовые ряды с положительными членами. Признак Даламбера.
Пусть задан ряд ∑ Un 0 (2)
(1)Необходимый признак.
Теорема1: if ряд(2)-сходится,
то
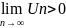 .
.
Доказательство: т.к. ряд сход-ся, то
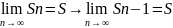
Sn=U1+…+Un; Sn-Sn-1=(Un+…+Un)-(Un+…Un-1)=Un.


Однако этот признак не является необходимым.
Рассмотрим ряд:
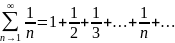 -гармонический
-гармонический
Покажем, что этот ряд расходится.
Для док-ва заменим некот. Числами и
покажем, что даже сумма меньше слагаемых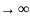
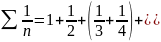
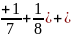 )+..
)+..
Раскрыв скобки, заменим слагаемые последним.


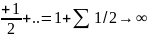
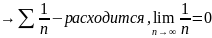
(2)Признаки сравнения. Формула Лемма.
Если всем част. Un суммы Sn огранич. одним и тем же числом m.
Доказ-во: if Sn‹M,
то (2) сх-ся и
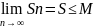
Теорема 2: !
 числами
и
числами
и
 Un≤Bn
Un≤Bn
1)if
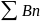 -сходится,
то
-сходится,
то
 -сходится
-сходится
2)if -расходится, то -расход.
Док-во:
Пусть ряд Bn расходится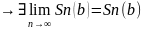
Т.к. Sn(b)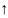 ,
то Sn(b)
S(b)
,
то Sn(b)
S(b)
Покажем, что Sn(u) имеет предел:
Sn(u)=u1+u2+..+un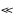 b1+b2+..+bn=Sn(b)
S(b)
b1+b2+..+bn=Sn(b)
S(b) Sn(u)
и Sn(u)
S(b)
Sn(u)
и Sn(u)
S(b)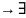 +
+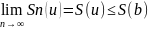
!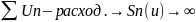
Т.к.
Sn(u)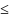 Sn(b)
Sn(b)
Sn(b)
Sn(b)
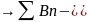 расход-ся.
Ч.Т.Д.
расход-ся.
Ч.Т.Д.
Теорема 3: Предельный признак сравнения.
!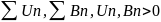
If
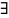 -т
-т
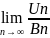 =A
=A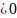 ,то
эти 2 ряда сходятся одновременно,т.е.1
из них сход.то и другой тоже.
,то
эти 2 ряда сходятся одновременно,т.е.1
из них сход.то и другой тоже.
Доказ-во: по определению пределов
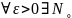 :
: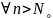 │
│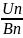 -A│
-A│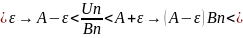
Un
(A+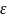 )Bn/
)Bn/
можно выбрать наст. Маленьким, чтобы(A- ) .
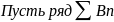 -сходится.
Т.к. Un
(A+
)Bn,
то Th2
-сходится.
Т.к. Un
(A+
)Bn,
то Th2
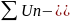 сходится
сходится
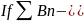 расходится,
то т.к. (A-
)Bn
Un,
то Th2
-расход.
Т.е. эти ряды сходятся одновременно.
Ч.Т.Д.
расходится,
то т.к. (A-
)Bn
Un,
то Th2
-расход.
Т.е. эти ряды сходятся одновременно.
Ч.Т.Д.
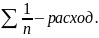
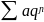 -
сход-ся │q│
,
расх. │q│
-
сход-ся │q│
,
расх. │q│
3)Пр-и Даламбера
Th4: ! (2) если
-т
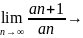
q сходится
сходится
q 1, расходится
q=1, ??

Доказ-во:1) q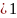 По опред. Предела т.к.
По опред. Предела т.к.
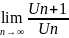 =q
=q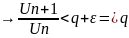 ,
при этом
можем подобрать так, что
,
при этом
можем подобрать так, что

Т.к. конечное число не влияет на него
можем считать, что это неравенство
выполнено, начин с n=1,
тогда

 =
q,
=
q,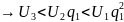
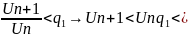
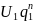 ,т.к.
│
,т.к.
│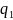 │
1,
то
│
1,
то
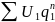 -сход.
Th2
-сход.
Доказ-во: 2) ! q
,
тогда начин с некот-го номера n:
-сход.
Th2
-сход.
Доказ-во: 2) ! q
,
тогда начин с некот-го номера n:
 ч.т.д.
ч.т.д.
Билет24(разложение функций в степенные ряды:ряд Тейлора и маклорена)
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
![]()
![]()
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1)![]() ,
где f(x) - функция, имеющая при х=а производные
всех порядков. Rn
- остаточный член в ряде Тейлора
определяется выражением
,
где f(x) - функция, имеющая при х=а производные
всех порядков. Rn
- остаточный член в ряде Тейлора
определяется выражением
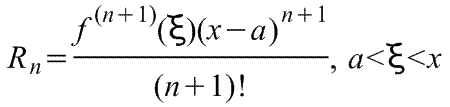
2)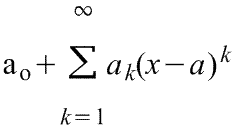
k-тый коэффициент (при хk) ряда определяется формулой
![]()
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при
a=0
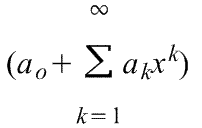
члены ряда определяются по формуле
![]()
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
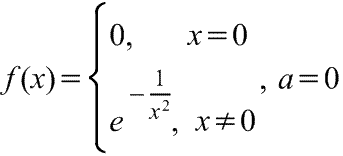
Ряды Тейлора применяются при аппроксимации ( приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
![]()
![]()
![]()
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:
1)![]() , где f(x) - функция, имеющая при а=0
производные всех порядков. Rn
- остаточный член в ряде Маклорена
(=Макларена) (Тейлора при а=0)определяется
выражением
, где f(x) - функция, имеющая при а=0
производные всех порядков. Rn
- остаточный член в ряде Маклорена
(=Макларена) (Тейлора при а=0)определяется
выражением
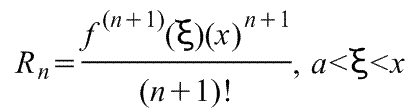
2)
k-тый коэффициент (при хk) ряда определяется формулой
Ряды Маклорена являются частным случаем рядов Тейлора.
Условия применния рядов Маклорена (=Макларена).
1) Для того, чтобы функция f(x) могла быть разложена в ряд Маклорена (=Макларена) на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Маклорена (=Макларена) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2) Необходимо чтобы существовали производные для данной функции в точке а=0, в окрестности которой мы собираемся строить ряд Маклорена (=Макларена).
Численное интегрирование с использованием рядов Маклорена (=Макларена).
Значения многих интегралов нельзя найти с помощью каких-либо аналитических методов. Мы уже рассказывали о вычислении таких интегралов с помощью формулы трапеций, формулы Симпсона. Другой метод нахождения числового значения определенного интеграла - выражение функции в виде ряда Маклорена (=Макларена) с последующим поочередным интегрированием каждого члена.
